Gelöste Aufgaben/Buck

Aufgabenstellung

Bei der Modellbildung für das Knicken von Stäben - also dem Stabilitätsverlust von Stäben durch seitliches Ausweichen unter axialer Druckbeanspruchung - gehen die Ansätze in Lehrbüchern und für Anwendungen in Finite-Elemente-Methoden unterschieldliche Wege.

Caption

Gesucht sind die Ansätze für die Berechnung der kritischen Drucklast ausgehen von

• dem Kräfte-Gleichgewicht am ausgelenkten System und
• dem Prinzip der virtuellen Verrückungen mit großen Dehnungen.

Das soll hier für den ersten Eulerschen Knickfall passieren. Ziel ist es, die Vorgehensweisen beider Ansätze einmal im Vergleich darzustellen. Der Fokus liegt dabei auf der Anwendung für Finite-Elemente-Methoden - also dem Prinzip der virtuellen Verrückungen mit großen Dehnungen.

Ansatz mit dem Kräftegleichgewicht am ausgelenkten System

Für das Verständnis des Phänomens "Knicken" ist es sinnvoll, die Zusammenhänge zwischen Koordinaten und Kräften anhand von Überlegungen zum Kräftegleichgewicht aufzuzeigen.

Dafür gehen wir von einem Stabelement der Länge $\mathrm{\Delta }x$ aus und tragen die Koordinaten $w(x),\phi (x)$ sowie die Schnittlasten $N(x),Q(x),M(x)$ in einem Freikörperbild an:

Schnittlasten am ausgelenkten Stab-Element.

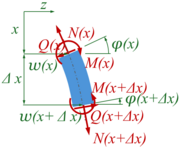
Wir finden

$\begin{array}{lll}\sum F_{x,i}=0& :& N(x+\mathrm{\Delta }x)\cos (\phi (x+\mathrm{\Delta }x))-N(x)\cos (\phi (x))-Q(x+\mathrm{\Delta }x)\sin (\phi (x+\mathrm{\Delta }x))+Q(x)\sin (\phi (x))=0,\\ \sum F_{z,i}=0& :& Q(x+\mathrm{\Delta }x)\cos (\phi (x+\mathrm{\Delta }x))-Q(x)\cos (\phi (x))+N(x+\mathrm{\Delta }x)\sin (\phi (x+\mathrm{\Delta }x))-N(x)\sin (\phi (x))=0,\\ \sum M^{x+\mathrm{\Delta }x}=0& :& M(x+\mathrm{\Delta }x)-M(x)+N(x)\sin (\phi (x))\mathrm{\Delta }x-N(x)\cos (\phi (x))(w(x+\mathrm{\Delta }x)-w(x))+Q(x)\cos (\phi (x))\mathrm{\Delta }x+Q(x)\sin (\phi (x))(w(x+\mathrm{\Delta }x)-w(x)).\end{array}$

Teilen durch $\mathrm{\Delta }x$ und der Grenzwert-Übergang von $\mathrm{\Delta }x\to dx$ liefert due differentiallen Gleichgewichtsbedingungen

$\begin{array}{l}\frac{d}{dx}(N\cos (\phi ))-\frac{d}{dx}(Q\sin (\phi ))=0\\ \frac{d}{dx}(Q\cos (\phi )+\frac{d}{dx}(N\sin (\phi )=0\\ \frac{d}{dx}\left(M\right)+N\sin (\phi )+Q\cos (\phi )+\frac{d}{dx}w(-N\cos (\phi )+Q\sin (\phi ))=0\end{array}$

Mit etwas Übersicht können wir die drei Gleichungen stark vereinfachen, wenn wir die dritte Gleichung nach $x$ ableiten. Dann nutzen wir die ersten beiden Gleichungen, um sie stark zu vereinfachen:

$\begin{array}{l}\frac{d^2}{d{x}^2}\left(M\right)+\underset{=0\text{ wg. Gleichung 2 oben}}{\underbrace{\frac{d}{dx}(N\sin (\phi )+Q\cos (\phi ))}}+\frac{d^2}{d{x}^2}w(-N\cos (\phi )+Q\sin (\phi ))+\frac{d}{dx}w\underset{=0\text{ wg. Gleichung 1 oben}}{\underbrace{\frac{d}{dx}(-N\cos (\phi )+Q\sin (\phi ))}}=0\end{array}$

Wir gehen weiter davon aus, dass wir in dieser Gleichung $Q\sin (\phi )\approx 0$ und $-N\cos (\phi )\approx P$ setzen dürfen - die Querkraft wird klein gegenüber der Normalkräft sein, und die Normalkraft setzen wir zur äußeren, eingeprägten Druckkraft $P$.

Dann erfasst die Differentialbeziehung

$M^{″}+P\cdot w^{″}=0$

das Knickproblem. Für den Euler-Bernoulli-Balken mit konstanter Querschnittsfläche gilt demnach für die Aulenkung

$EI{w}^{IV}+P\cdot w^{″}=0.$

Diese lineare Differentialgleichung liefer mit dem Ansatz $w(x)=e^{\kappa x}$ die vier Eigenwerte

$\begin{array}{lll}{\kappa }_1& =& 0,\\ {\kappa }_2& =& 0,\\ {\kappa }_3& =& +j\cdot \sqrt{\frac{P}{EI}},\\ {\kappa }_4& =& -j\cdot \sqrt{\frac{P}{EI}},\\ \end{array}$

mit $j:=\sqrt{-1}$. Die Lösung der Differentialbeziehung ist demnach

$w(x)=W_1+W_2\cdot x+W_3\cdot \sin ({\kappa }_{3}x)+W_4\cdot \cos ({\kappa }_{4}x)$

mit den reelwertigen Integrationskonstanten $W_1,W_2,W_3,W_4$, die aus den Randbedingungen des Problems kommen. Für den ersten Eulerschen Knickfall oben gilt

$\begin{array}{lll}w(0)& =& 0\\ w^{\prime }(0)& =& 0\\ -EI{w}^{″}(\ell )& =& 0\\ -EI{w}^{‴}(\ell )+P{w}^{\prime }(\ell )& =& 0,\\ \end{array}$

also in Matrixschreibweise

$\underset{\underset{\_}{\underset{\_}{A}}}{\underbrace{\left(\begin{array}{cccc}1& 0& 0& 1\\ 0& 1& \kappa & 0\\ 0& 0& {\kappa }^{2}EI\sin (\kappa \ell )& {\kappa }^{2}EI\cos (\kappa \ell )\\ 0& -{\kappa }^{2}EI& 0& 0\\ \end{array}\right)}}\cdot \left(\begin{array}{c}{W}_1\\ W_2\\ W_3\\ W_4\\ \end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 0\\ 0\\ \end{array}\right)$

Dieses homogene Gleichungssystem hat Lösungen, wenn

$\text{det}(\underset{\_}{\underset{\_}{A}})={\kappa }^5\cos (\kappa \ell )\stackrel{!}{=}0$

ist, also

${\kappa }_0=0,{\kappa }_1\ell =\pm \frac{\pi }{2},{\kappa }_2\ell =\pm \frac{3\pi }{2},\dots$.

Der kritische Wert von $\kappa$ ist der niedrigeste, zur nicht-trivialen Lösung gehörende Wert ${\kappa }_1$ und damit

$P_{krit}=\frac{{\pi }^{2}EI}{4{\ell }^2}$.

Dieser Lösungsansatz - Gleichgewicht am ausgelenkten System - funktioniert allerdings nur gut für sehr einfache Systeme. Für technsche Systeme brauchen wir einen Ansatz, der immer funktionert und bei dem man kein Freikörperbild zeichnen muss. Das geth mit dem Prinzip der virtuellen Verrückungen.

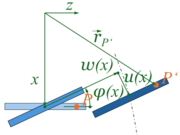
Ansatz mit dem Prinzip der virtuellen Verrückungen mit großen Dehnungen

Für den Einsatz in Finite-Elemente-Methoden ist der Ansatz über ein Kräftegleichgewicht wie oben nicht möglich und sinnvoll: im Allgemeinen kann man für die zu untersuchenden Systeme kein Kräftegleichgewicht aufstellen. Hier geht man vom Prinzip der virtuellen Verrückungen aus, wobei in der virtuellen Formänderungsarbeit

$\delta \mathrm{\Pi }=\underset{V}{\int }\underset{\_}{\sigma }\cdot \delta \underset{\_}{\epsilon }dV$

die Dehnung $\underset{\_}{\epsilon }$ nichtlineare Anteile der Koordinaten der Verformung enthält.

Kinemtik der Auslenkung eines Stab-Querschnitts $x$.

Lösung mit Maxima

Lorem Ipsum ....

tmp

Title

Text

1+1

---

Links

• ...

Literature

• ...