Gelöste Aufgaben/Buck: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 13: | Zeile 13: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Bei der Modellbildung für das Knicken von Stäben - also dem Stabilitätsverlust von Stäben durch seitliches Ausweichen unter axialer Druckbeanspruchung - gehen die Ansätze in Lehrbüchern und | |||
für Anwendungen in Finite-Elemente-Methoden unterschieldliche Wege. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Buck-01.png|100px|left|mini|Caption]] | [[Datei:Buck-01.png|100px|left|mini|Caption]] | ||
Gesucht ist | Gesucht sind die Ansätze für die Berechnung der kritischen Drucklast ausgehen von | ||
* dem Kräfte-Gleichgewicht am ausgelenkten System und | |||
* dem Prinzip der virtuellen Verrückungen mit großen Dehnungen. | |||
Ziel ist es, die Vorgehensweisen beider Ansätze einmal im Vergleich darzustellen. Der Fokus liegt dabei auf der Anwendung für Finite-Elemente-Methoden - also dem Prinzip der virtuellen Verrückungen mit großen Dehnungen. | |||
</onlyinclude> | </onlyinclude> | ||
== Ansatz mit dem Kräftegleichgewicht am ausgelenkten System == | |||
Für das Verständnis des Phänomens "Knicken" ist es sinnvoll, die Zusammenhänge zwischen Koordinaten und Kräften anhand von Überlegungen zum Kräftegleichgewicht aufzuzeigen. | |||
Dafür gehen wir von einem Stabelement der Länge <math\Delta x</math> aus und tragen die Koordinaten <math>w(x), \varphi(x)</math> sowie die Schnittlasten <math>N(x),Q(x),M(x)</math> in einem Freikörperbild an: | |||
[[Datei:Buck-11.png|180px|right|mini|Schnittlasten am ausgelenkten Stab-Element.]] | |||
Wir finden | |||
<math> | |||
\begin{array}{lll} | |||
\sum F_{x,i} = 0 &:& N(x+\Delta x) \; \cos(\varphi(x+\Delta x)) - N(x) \; \cos(\varphi(x)) | |||
-Q(x+\Delta x) \; \sin(\varphi(x+\Delta x)) + Q(x) \; \sin(\varphi(x)) = 0,\\ | |||
\sum F_{z,i} = 0 &:& Q(x+\Delta x) \; \cos(\varphi(x+\Delta x)) - Q(x) \; \cos(\varphi(x)) | |||
+N(x+\Delta x) \; \sin(\varphi(x+\Delta x)) - N(x) \; \sin(\varphi(x)) = 0,\\ | |||
\sum M^{x+\Delta x} = 0 &:& M(x+\Delta x) - M(x) | |||
+N(x)\;\sin(\varphi(x))\;\Delta x -N(x)\;\cos(\varphi(x))\;\left(w(x+\Delta x)-w(x)\right) | |||
+Q(x)\;\cos(\varphi(x))\;\Delta x +Q(x)\;\sin(\varphi(x))\;\left(w(x+\Delta x)-w(x)\right). | |||
\end{array} | |||
</math> | |||
Teilen durch <math>\Delta x</math> und der Grenzwert-Übergang von <math>\Delta x \rightarrow dx</math> liefert due differentiallen Gleichgewichtsbedingungen | |||
<math> | |||
\begin{array}{l} | |||
\frac{d}{dx}\left(N\; \cos(\varphi)\right)-\frac{d}{dx}\left(Q\; \sin(\varphi)\right) = 0\\ | |||
\frac{d}{dx}\left(Q\; \cos(\varphi\right) +\frac{d}{dx}\left(N\;\sin(\varphi\right) = 0\\ | |||
\frac{d}{dx}\left(M\right) +N\;\sin(\varphi)+Q\;\cos(\varphi) | |||
+ \frac{d}{dx}\;w \; \left(-N\;\cos(\varphi) + Q\;\sin(\varphi)\right) = 0 | |||
\end{array} | |||
</math> | |||
== Ansatz mit dem Prinzip der virtuellen Verrückungen mit großen Dehnungen == | |||
Für den Einsatz in Finite-Elemente-Methoden ist der Ansatz über ein Kräftegleichgewicht wie oben nicht möglich und sinnvoll: im Allgemeinen kann man für die zu untersuchenden Systeme kein Kräftegleichgewicht aufstellen. Hier geht man vom Prinzip der virtuellen Verrückungen aus, wobei in der virtuellen Formänderungsarbeit | |||
::<math>\delta \Pi = \int_V \underline{\sigma} \cdot \delta\underline{\varepsilon} dV</math> | |||
die Dehnung <math>\underline{\varepsilon}</math> nichtlineare Anteile der Koordinaten der Verformung enthält. | |||
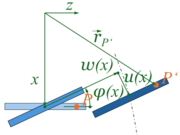
[[Datei:Buck-12.png|180px|left|mini|Kinemtik der Auslenkung eines Stab-Querschnitts <math>x</math>.]] | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
| Zeile 26: | Zeile 73: | ||
Version vom 18. November 2025, 14:35 Uhr
Aufgabenstellung
Bei der Modellbildung für das Knicken von Stäben - also dem Stabilitätsverlust von Stäben durch seitliches Ausweichen unter axialer Druckbeanspruchung - gehen die Ansätze in Lehrbüchern und für Anwendungen in Finite-Elemente-Methoden unterschieldliche Wege.

Gesucht sind die Ansätze für die Berechnung der kritischen Drucklast ausgehen von
- dem Kräfte-Gleichgewicht am ausgelenkten System und
- dem Prinzip der virtuellen Verrückungen mit großen Dehnungen.
Ziel ist es, die Vorgehensweisen beider Ansätze einmal im Vergleich darzustellen. Der Fokus liegt dabei auf der Anwendung für Finite-Elemente-Methoden - also dem Prinzip der virtuellen Verrückungen mit großen Dehnungen.
Ansatz mit dem Kräftegleichgewicht am ausgelenkten System
Für das Verständnis des Phänomens "Knicken" ist es sinnvoll, die Zusammenhänge zwischen Koordinaten und Kräften anhand von Überlegungen zum Kräftegleichgewicht aufzuzeigen.
Dafür gehen wir von einem Stabelement der Länge <math\Delta x</math> aus und tragen die Koordinaten sowie die Schnittlasten in einem Freikörperbild an:
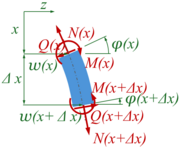
Wir finden
Teilen durch und der Grenzwert-Übergang von liefert due differentiallen Gleichgewichtsbedingungen
Ansatz mit dem Prinzip der virtuellen Verrückungen mit großen Dehnungen
Für den Einsatz in Finite-Elemente-Methoden ist der Ansatz über ein Kräftegleichgewicht wie oben nicht möglich und sinnvoll: im Allgemeinen kann man für die zu untersuchenden Systeme kein Kräftegleichgewicht aufstellen. Hier geht man vom Prinzip der virtuellen Verrückungen aus, wobei in der virtuellen Formänderungsarbeit
die Dehnung nichtlineare Anteile der Koordinaten der Verformung enthält.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Title
Text
1+1
Links
- ...
Literature
- ...