Gelöste Aufgaben/Stor: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 54: | Zeile 54: | ||
{{MyCodeBlock|title=Modellteile für Fahrbahn und Seile | {{MyCodeBlock|title=Modellteile für Fahrbahn und Seile | ||
|text= | |text= | ||
Die Gleichgewichtsbedingung formulieren wir mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe_der_Analytischen_Mechanik/Prinzip_der_virtuellen_Verrückungen|Prinzip der virtuellen Verrückungen]] zu | |||
::<math>\begin{array}{lll}\delta W & = & \delta W^a - \delta \Pi\\ | |||
& = & 0 \end{array}</math>. | |||
Die virtuellen Arbeiten setzen sich dabei additiv aus den Beiträgen der 14 Elemente zusammen, also | |||
::<math>\delta \Pi = \sum_{e=1}^{14} \delta \Pi_e</math> und <math>\delta W^a = \sum_{e=1}^{14} \delta W^a_e</math> | |||
Die Gesamt-Steifigkeitsmatrix des Systems komponieren aus der | Die Gesamt-Steifigkeitsmatrix des Systems komponieren aus der | ||
| Zeile 92: | Zeile 101: | ||
\right)</math> | \right)</math> | ||
Die Gesamt-Steifigkeitsmartix entsteht, indem wir die einzelnen Anteile der 17 Elemente zu einer leeren <math>28 \times 28</math> - Matrix hinzuaddieren. | Die Gesamt-Steifigkeitsmartix entsteht, indem wir die einzelnen Anteile der 17 Elemente zu einer leeren <math>28 \times 28</math> - Matrix hinzuaddieren. Die folgenden Bilder zeigen, wie: | ||
[[Datei:Stor-12.png|700px|left|mini|Struktur des mathematischen Modells.]] | [[Datei:Stor-12.png|700px|left|mini|Struktur des mathematischen Modells.]] | ||
[[Datei:Stor-12-legend.png|120px|right|mini|Farbkodierung des Modells.]] | |||
Dabei müssen die einzelnen Beiträge passend zu den Gesamtmatrizen hinzugefügt werden. | |||
Dies zeigen wir hier am Beispiel der Gesamt-Steifigkeitsmatrix für das Hinzufügen von Element 14. | |||
Die virtuelle Formänderungsenergie von ELement 14 ist | |||
::<math>\delta\Pi_{14} = \left(\delta W_3 \delta W_{10}\right)\cdot \frac{E A_{14}}{\ell_{14}} \left(\begin{array}{rr}1&-1\\-1&1\end{array}\right)\cdot\left(\begin{array}{r}W_3\\W_{10}\end{array} \right)</math> | |||
Wir erhalten diese Form, indem wir einen vertikalen Stab über <math>\xi_x=0,\xi_y=1</math> in | |||
[[Gelöste_Aufgaben/T312]] und | |||
definieren. | |||
[[Datei:Stor-13.png|250px|left|mini|Herausgehoben: die Beiträge von Element 14.]] | |||
|code= | |code= | ||
| Zeile 107: | Zeile 129: | ||
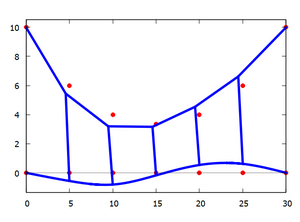
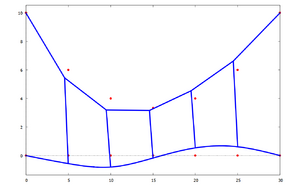
[[Datei:Stor-21.png|300px|left|mini|Verformte Brücke.]] | [[Datei:Stor-21.png|300px|left|mini|Verformte Brücke.]] | ||
Version vom 7. Oktober 2025, 07:57 Uhr
Aufgabenstellung
Der Mittelteil einer einfachen Hängebrücke besteht aus zwei Pylonen, an denen die Tragseile (Cable) geführt werden, an denen der Fahrbahnträger (Deck) aufgehängt ist.
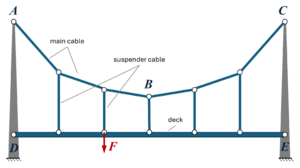
Gesucht ist ein einfaches, lineares FE-Modell für statische Spannungen und Verformungen der Seile und Fahrbahn. Die Verformung der Pylone soll icht berücksichtigt werden.
Die Spannweite der Brücke beträgt =30m, die Pylonhöhe AD beträgt =10m. Die Brücke wird durch ihr Gewicht und zusätzlichen Kräften zwischen D und E von =10kN an den Verbindungen mit den vertikalen Seilen belastet. Die Abmessungen von Seilen und Fahrbahn-Querschnitt wählen wir passend.
Strukturieren
Gesucht ist ein mathematisches Modell für die Hängebrücke - bestehen aus Fahrbahn, Tragseil und Hängeseilen. Wir gehen davon aus, dass die Anteile der Biegesteifigkeit der Seile vernachlässigbar sind - wir sie also als Dehnstäbe wie in einem Fachwerk modellieren können. Tun wir das nicht, werden die Auslenkungen der Tragseile im linearen Ansatz sehr groß und werden erst durch die Saitenspannungen - also nichtlineare Effekte - wieder auf ein sinnvolles Maß reduziert.
Die Fahrbahn modelleiren wir als Euler-Bernoulli-Balken - Verschiebungen der Querschnittsflächen des Balkens vernachlässigen wir.
Auf die Struktur wirken ihre Gewichtskräfte und eine Einzellast. Das resultierende Gleichungssystem des FE-Modells für die Koordinaten der Auslenkung der Brücke ist von der Form
mit der Steifigkeitsmatrix , der Spaltenmatrix der unbekannten Koordinaten und der Spaltenmatrix der äußeren Lasten .
Der Einfachheit halber wählen wir jeweils nur ein Finites Element zwischen den Stoßpunkten der Brückenteile.
Aufgabenstellung konkretisieren
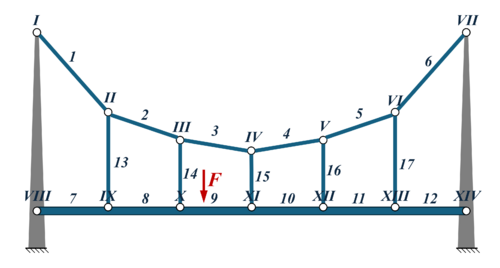
Die Hängebrücke teilen wir somit in 12 Elemente ein. Dies sind
- die Elemente 1, ... 6 für das Tragseil
- die Elemente 7, ... 12 für die Fahrbahn und
- die Elemente 13, ... 17 für die Hängeseile.
Mit den römischen Ziffern I ... XIV kennzeichnen wir die Knotenpunkte zwischen den Elementen.
Koordinten des Modells sind damit die horizontalen und vertikalen Auslenkungen der Knoten I ... VII und die vertiakle Auslenkung und Kippung der Knoten in VIII ... XIV.
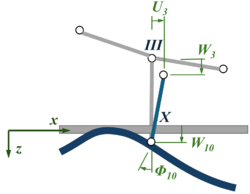
Modellteile für Fahrbahn und Seile
Die Gleichgewichtsbedingung formulieren wir mit dem Prinzip der virtuellen Verrückungen zu
- .
Die virtuellen Arbeiten setzen sich dabei additiv aus den Beiträgen der 14 Elemente zusammen, also
- und
Die Gesamt-Steifigkeitsmatrix des Systems komponieren aus der Elementsteifigkeitsmatrix des Dehnstabes und Elementsteifigkeitsmatrix des Euler-Bernoulli-Balkens.
Wir schreiben zunächst die Koordinaten der Verschiebung und Verdrehung der Knoten des Systems hin, hier
Die Gesamt-Steifigkeitsmartix entsteht, indem wir die einzelnen Anteile der 17 Elemente zu einer leeren - Matrix hinzuaddieren. Die folgenden Bilder zeigen, wie:
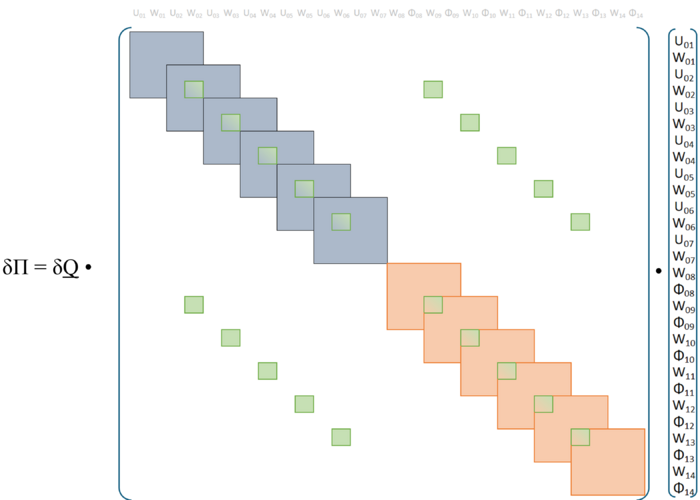
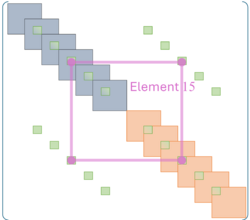
Dabei müssen die einzelnen Beiträge passend zu den Gesamtmatrizen hinzugefügt werden. Dies zeigen wir hier am Beispiel der Gesamt-Steifigkeitsmatrix für das Hinzufügen von Element 14.
Die virtuelle Formänderungsenergie von ELement 14 ist
Wir erhalten diese Form, indem wir einen vertikalen Stab über in Gelöste_Aufgaben/T312 und definieren.
1+1
System strukturieren
Modellieren
Virtuelle Formänderungsenergie
Virtuelle Arbeiten der äußeren Kräfte am System
Lösen
Ausdeuten
Links
- ...
Literature
- ...