Gelöste Aufgaben/Stor: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Der Mittelteil einer | Der Mittelteil einer einfachen Hängebrücke besteht aus zwei Pylonen, an denen die Tragseile (Cable) geführt werden, an denen der Fahrbahnträger (Deck) aufgehängt ist. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Stor-01.png|300px|left|mini|Der Mittelteil einer Hängebrücke]] | [[Datei:Stor-01.png|300px|left|mini|Der Mittelteil einer Hängebrücke]] | ||
Gesucht ist ein FE-Modell für statische Spannungen und Verformungen der Seile und Fahrbahn. | Gesucht ist ein einfaches FE-Modell für statische Spannungen und Verformungen der Seile und Fahrbahn. | ||
Die Verformung der Pylone | Die Verformung der Pylone soll icht berücksichtigt werden. | ||
</onlyinclude> | </onlyinclude> | ||
Die Spannweite der Brücke beträgt <math>L</math>=30m, die Pylonhöhe AD beträgt <math>H</math>=10m. Die Brücke wird durch ihr | Die Spannweite der Brücke beträgt <math>L</math>=30m, die Pylonhöhe AD beträgt <math>H</math>=10m. Die Brücke wird durch ihr | ||
Gewicht und zusätzlichen Kräften zwischen D und E von <math>F</math>=10kN an den Verbindungen mit den vertikalen Seilen belastet. | Gewicht und zusätzlichen Kräften zwischen D und E von <math>F</math>=10kN an den Verbindungen mit den vertikalen Seilen belastet. Die Abmessungen von Seilen und Fahrbahn-Querschnitt wählen wir passend. | ||
== Strukturieren == | == Strukturieren == | ||
Wir suchen nach dem mathematischen Modell für die Hängebrücke - bestehen aus dem Fahrbahn, dem Tragseil und den Hängeseilen. | |||
Wir gehen davon aus, dass die Biegesteifigkeit der Seile vernachlässigbar ist - wir sie also als Dehnstäbe modellieren können. | |||
Auf die Struktur wirken ihre Gewichtskräfte und eine Einzellast. Das resultierende Gleichungssystem des FE-Modells für die Koordinaten der Auslenkung der Brücke ist von der Form | |||
::<math>\underline{\underline{K}}\cdot\underline{Q}=\underline{P}</math> | |||
mit der Steifigkeitsmatrix <math>\underline{\underline{K}}</math>, der Spaltenmatrix der unbekannten Koordinaten <math>\underline{Q}</math> und der Spaltenmatrix der äußeren Lasten <math>\underline{P}</math>. | |||
Der Einfachheit halber wählen wir jeweils nur ein Finites Element zwischen den Stoßpunkten der Brückenteile. | |||
=== Aufgabenstellung konkretisieren === | |||
Die Hängebrücke teilen wir somit in 12 Elemente ein. Dies sind | |||
* die Elemente 1, ... 6 für das Tragseil | |||
* die Elemente 7, ... 12 für die Fahrbahn und | |||
* die Elemente 13, ... 17 für die Hängeseile. | |||
Mit den römischen Ziffern I ... 14 kennzeichnen wir die Knotenpunkte zwischen den Elementen. | |||
[[Datei:Stor-11.png|500px|left|mini|Bezeichnung der Elemente und Knoten.]] | [[Datei:Stor-11.png|500px|left|mini|Bezeichnung der Elemente und Knoten.]] | ||
| Zeile 38: | Zeile 56: | ||
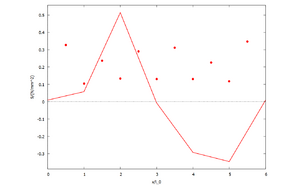
[[Datei:Stor-22.png|300px|left|mini|Spannungen in allen Bauteilen.]] | [[Datei:Stor-22.png|300px|left|mini|Spannungen in allen Bauteilen.]] | ||
Version vom 5. Oktober 2025, 07:18 Uhr
Aufgabenstellung
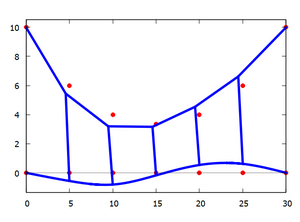
Der Mittelteil einer einfachen Hängebrücke besteht aus zwei Pylonen, an denen die Tragseile (Cable) geführt werden, an denen der Fahrbahnträger (Deck) aufgehängt ist.
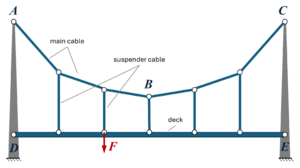
Gesucht ist ein einfaches FE-Modell für statische Spannungen und Verformungen der Seile und Fahrbahn. Die Verformung der Pylone soll icht berücksichtigt werden.
Die Spannweite der Brücke beträgt =30m, die Pylonhöhe AD beträgt =10m. Die Brücke wird durch ihr Gewicht und zusätzlichen Kräften zwischen D und E von =10kN an den Verbindungen mit den vertikalen Seilen belastet. Die Abmessungen von Seilen und Fahrbahn-Querschnitt wählen wir passend.
Strukturieren
Wir suchen nach dem mathematischen Modell für die Hängebrücke - bestehen aus dem Fahrbahn, dem Tragseil und den Hängeseilen. Wir gehen davon aus, dass die Biegesteifigkeit der Seile vernachlässigbar ist - wir sie also als Dehnstäbe modellieren können.
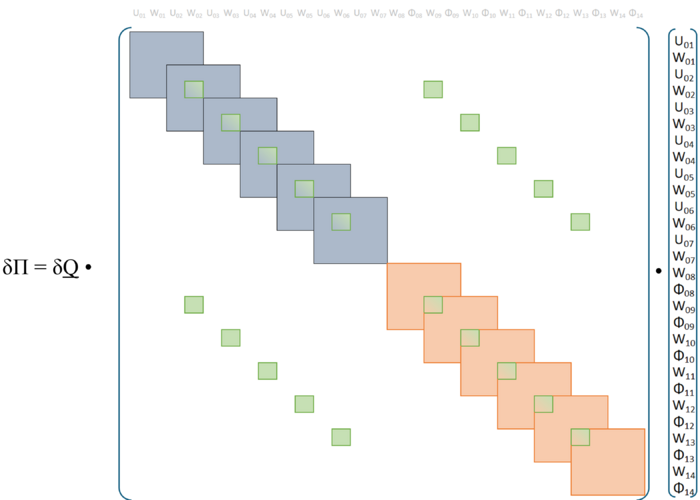
Auf die Struktur wirken ihre Gewichtskräfte und eine Einzellast. Das resultierende Gleichungssystem des FE-Modells für die Koordinaten der Auslenkung der Brücke ist von der Form
mit der Steifigkeitsmatrix , der Spaltenmatrix der unbekannten Koordinaten und der Spaltenmatrix der äußeren Lasten .
Der Einfachheit halber wählen wir jeweils nur ein Finites Element zwischen den Stoßpunkten der Brückenteile.
Aufgabenstellung konkretisieren
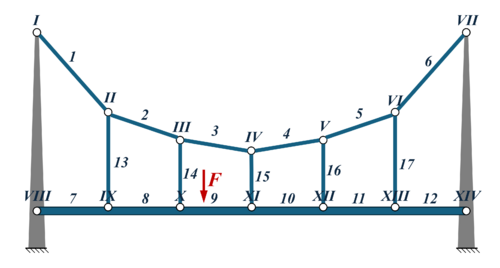
Die Hängebrücke teilen wir somit in 12 Elemente ein. Dies sind
- die Elemente 1, ... 6 für das Tragseil
- die Elemente 7, ... 12 für die Fahrbahn und
- die Elemente 13, ... 17 für die Hängeseile.
Mit den römischen Ziffern I ... 14 kennzeichnen wir die Knotenpunkte zwischen den Elementen.
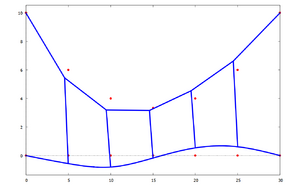
System strukturieren
Modellieren
Virtuelle Formänderungsenergie
Virtuelle Arbeiten der äußeren Kräfte am System
Lösen
Ausdeuten
Title
Text
1+1
Links
- ...
Literature
- ...