Gelöste Aufgaben/MaMa

Aufgabenstellung

Ein Stab der Länge $3a$ und Biegesteifigkeit $EI$ ist links fest eingespannt und wird bei 2/3 seiner Länger durch ein gelenkiges Lager gestützt. Zwischen dem freien rechten Rand und dem gelenkigen Lager wirkt eine konstante Streckenlast $q_{0}$.

Lageplan

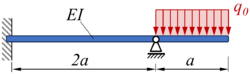
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken und die Verläufe der Schnittgrößen. Im Vordergrund der Ausarbeitung steht das Zusammenspiel von Maxima (Computeralgebra) und Matlab (Numerik) zum Aufstellen, Verwalten und Lösen des linearen Gleichungssystems.

Die Aufgabe ist einfach genug, um sie analytisch mit Maxima allein zu lösen. Hier geht es aber darum, die "Zusammenarbeit" zwischen den beiden Software-Paketen exemplarisch vorzustellen. Dieses Zusammenspiel wird dann interessant, wenn die Anzahl der Gleichungen groß wird - typischer weise > 50. Dann ist eine algebraische Lösung oft nicht mehr möglich. Maxima eignet sich dann hervorragend für das Aufstellen und Verwalten der Gleichungen. Die konsolidierten Gleichungen werden dann zur numerischen Lösung an Matlab übergeben. Wie das geht, zeigen wir im Folgenden.

Lösung mit Maxima und Matlab

Im folgenden finden Sie die Skripte für Maxima und Matlab, mit denen diese Aufgabe bearbeitet wurde.

Declarations

Wir zeichnen zunächst die Berieche, Knoten und Koordinaten aus:

Bezeichnung für Bereiche und Knoten einführen.

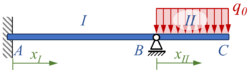
Für Bereich $I$ führen wir die unabhängige Koordinate $x_{I}$ ein, für Bereich $II$ die Koordinate $x_{II}$. Die zwei Bereich haben die Längen

• $\ell _{I}$ und
• $\ell _{I}I$.

Um die gesuchte Lösung dimensionslos ansetzten zu können, wählen wir eine Vergleichslösung. Hier bietet sich der Kragbalken unter Streckenlast an. Diese liefert für die maximale Auslenkung von $w(x)$ und die maximlae Kippung der Querschnitte von $\phi (x)$

• $w_{ref}={\frac {q_{0}a^{4}}{8EI}}$ und
• $\varphi _{ref}={\frac {q_{0}a^{3}}{6EI}}$

Außerdem wählen wir

• $M_{ref}={\frac {q_{0}a^{2}}{2}}$ und
• $Q_{ref}=q_{0}a$

Boundary Value Problem

Das Randwertproblem wird im Feld von der Euler-Bernoulli-Differentialgleichung des Balkens beschreiben und an den Rändern durch kinematische oder Kraft-Randbedingungen.

Differentialgleichung des Euler-Bernoulli-Balkens

Die Gleichgewichtsbedingung am Balken führt auf die Differentialgleichung

$EIw^{IV}=q_{0}$

Deren allgemeine Lösung (also ohne Anpassung an Rand- und Übergangsbedingungen) ist

... für die Auslenkung des Querschnitts:	$EIw(x)={\frac {1}{24}}q_{0}x^{4}+{\frac {1}{6}}C_{3}x^{3}+{\frac {1}{2}}C_{2}x^{2}+C_{1}x+C_{0}$

mit den 4 Integrationskonstanten - und damit unseren Unbekannten je Abschnitt -

$C_{=},C_{1},C_{2}{\text{ und }}C_{3}$.

Aus Gleichgewichts- und Kinematik-Beziehungen kommen dann die weiteren Gleichungen

... für den Kippwinkel des Querschnitts:	$EI\varphi (x)=EI{\frac {dw}{dx}}=+{\frac {1}{6}}q_{0}x^{3}+{\frac {1}{2}}C_{3}x^{2}+C_{2}x+C_{1}$
... für das Biegemoment:	$M(x)=-EI{\frac {d^{2}w}{dx^{2}}}=-{\frac {1}{2}}q_{0}x^{2}-C_{3}x-C_{2}$ und
... für die Querkraft:	$Q(x)={\frac {dM}{dx}}=-q_{0}x-C_{3}$ und

In unserer Aufgabe haben wir zwei Bereiche - in B müssen wir diese allgemeinen Lösungen aneinander anstückeln. Um sie zu unterscheiden, hängen wir für jede Lösung den Index des Bereichs an, also

Bereich I $0<x_{I}<\ell _{I}$	Bereich II $0<x_{II}<\ell _{II}$
$EIw_{I}(x)={\frac {1}{24}}q_{I,0}x_{I}^{4}+{\frac {1}{6}}C_{I,3}x_{I}^{3}+{\frac {1}{2}}C_{I,2}x_{I}^{2}+C_{I,1}x+C_{I,0}$	$EIw_{II}(x)={\frac {1}{24}}q_{II,0}x_{I}^{4}+{\frac {1}{6}}C_{II,3}x_{I}^{3}+{\frac {1}{2}}C_{II,2}x_{I}^{2}+C_{II,1}x+C_{II,0}$

Und das gilt in gleicher Weise für die Gleichungen von $\varphi ,M,Q$.

Rand- und Übergangsbedingungen

Die Rand- und Übergangsbedingungen im Stab finden wir entweder aus kinematischen Überlegungen oder aus Gleichgewichtsbeziehungen mit den Schnittkräften des Balkens.

${\displaystyle }$ ${\displaystyle }$ ${\displaystyle }$ ${\displaystyle }$ ${\displaystyle }$

Title

Text

1+1

---

Links

• ...

Literature

• ...