Sources/Lexikon/Axiome der Statik: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{| class="wikitable" | |||
| | |||
| | |||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 7: | Zeile 9: | ||
| | | | ||
=== Axiom 1: === | === Axiom 1: === | ||
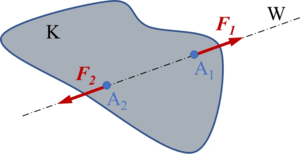
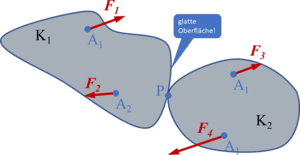
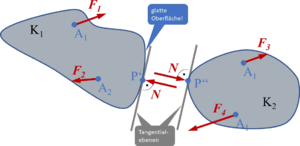
Ein freier, starrer Körper Κ ist unter der Wirkung von zwei Kräften | Ein freier, starrer Körper Κ ist unter der Wirkung von zwei Kräften <math display="inline">\vec{F}_1</math>, <math display="inline">\vec{F}_2</math> dann und nur dann im Gleichgewicht, wenn sie in die Verbindungslinie ihrer beiden Angriffspunkte ''A<sub>1</sub>'', ''A<sub>2</sub>'' fallen, entgegengesetzt orientiert und gleich groß sind. | ||
{| class="wikitable" | {| class="wikitable" | ||
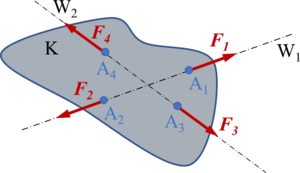
|[[Datei:AxiomeDerStatik-A1.png|mini|Bild A1-1: Körper im Gleichgewicht]] | |[[Datei:AxiomeDerStatik-A1.png|mini|Bild A1-1: Körper im Gleichgewicht]] | ||
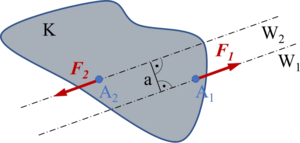
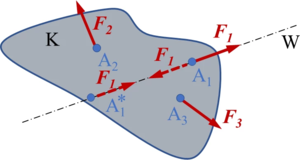
|[[Datei:AxiomeDerStatik-1-b.png|mini|Bild A1-2: Körper nicht im Gleichgewicht]] | |[[Datei:AxiomeDerStatik-1-b.png|mini|Bild A1-2: Körper nicht im Gleichgewicht]] | ||
|} | |} | ||
Formal bedeutet dies zweierlei (vgl. Bilder A1-1 und -2): Die Vektorsumme aus | Formal bedeutet dies zweierlei (vgl. Bilder A1-1 und -2): Die Vektorsumme aus <math display="inline">\vec{F}_1</math>, <math display="inline">\vec{F}_2</math> und der Abstand ''a'' müssen verschwinden. | ||
Durch die erste Gleichung wird der Teil des Axioms „entgegengesetzt orientiert und gleich groß" erfasst, erst mit ''a'' = 0 werden die Kräfte auch in die Verbindungslinie der beiden Angriffspunkte gezwungen. | Durch die erste Gleichung wird der Teil des Axioms „entgegengesetzt orientiert und gleich groß" erfasst, erst mit ''a'' = 0 werden die Kräfte auch in die Verbindungslinie der beiden Angriffspunkte gezwungen. | ||
| Zeile 26: | Zeile 28: | ||
| | | | ||
===Axiom 2:=== | ===Axiom 2:=== | ||
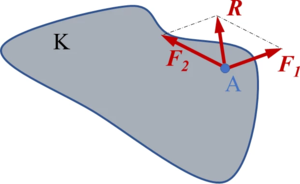
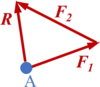
Greifen zwei | Greifen zwei Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> an einem gemeinsamen Angriffspunkt A an, so können sie durch eine Kraft <math display="inline">\vec{R}</math> ersetzt werden, die sich als die Diagonale des durch die beiden Kräfte aufgespannten Parallelogramms ergibt, Bild 3. | ||
Gemäß Bild 3, ist die Diagonale R die (geometrische) Summe der beiden | Gemäß Bild 3, ist die Diagonale <math display="inline">\vec{R}</math> die (geometrische) Summe der beiden Vektoren <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> : | ||
::<math>\vec{R} = \vec{F}_1+\vec{F}_2</math>. | ::<math>\vec{R} = \vec{F}_1+\vec{F}_2</math>. | ||
| Zeile 43: | Zeile 45: | ||
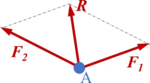
'''Definition:''' Gemäß dem Kräfteparallelogramm in Bild führt man <math display="inline">\vec{R}</math> als resultierende Kraft - kurz Resultierende - der beiden (Einzel-)Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> ein. Die Resultierende ersetzt die (Wirkung der) Einzelkräfte! | '''Definition:''' Gemäß dem Kräfteparallelogramm in Bild führt man <math display="inline">\vec{R}</math> als resultierende Kraft - kurz Resultierende - der beiden (Einzel-)Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> ein. Die Resultierende ersetzt die (Wirkung der) Einzelkräfte! | ||
{{MyNote|title= | {{MyNote|title=Hinweis 1:|text=Bildet man die Resultierende für zwei Kräfte in einem Lageplan oder Schnittbild, so muß man mit dem Kräfteparallelogramm und darf nicht mit dem Krafteck arbeiten.}} | ||
{{MyNote|title= | {{MyNote|title=Hinweis 2:|text=Man kann auch die Wirkung einer (resultierenden) Kraft <math display="inline">\vec{R}</math> gemäß Kräfteparallelogramm (Bild) durch die Wirkung der beiden Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> ersetzen. dann heißen <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> Komponenten von <math display="inline">\vec{R}</math>.}} | ||
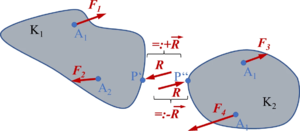
{{MyNote|title= | {{MyNote|title=Hinweis 3:|text=Die erste Gleichung von Axiom 1 kann man nun als <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> = <math display="inline">\vec{R}</math> und <math display="inline">\vec{R}</math> = <math display="inline">\vec{0}</math> interpretieren. Notwendig für das Gleichgewicht des in Bild 1-3-2 gezeigten Körpers ist es, daß die Resultierende der beiden Kräfte <math display="inline">\vec{F}_1</math> und <math display="inline">\vec{F}_2</math> verschwindet.}} | ||
|} | |} | ||