Gelöste Aufgaben/T3BP: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 35: | Zeile 35: | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text=Die Bewegungsgleichungen schreiben wir in Vektorschreibweise für Körper <i>i</i> als | ||
::<math> m_i \dot \ddot{\vec{u}}_i = \sum_{\ell=j,k} G\cdot \frac{\displaystyle m_i\cdot m_\ell}{\displaystyle r_{i,\ell}^2} \dot \vec{e}_{i,\ell} \text{ mit } | ::<math> m_i \dot \ddot{\vec{u}}_i = \sum_{\ell=j,k} G\cdot \frac{\displaystyle m_i\cdot m_\ell}{\displaystyle r_{i,\ell}^2} \dot \vec{e}_{i,\ell} \text{ mit } | ||
\vec{u}_i = \left(\vec{e}_x,\vec{e}_y,\vec{e}_z\right)\cdot \underbrace{\left(\begin{array}{l}u_x\\u_y\\u_z\end{array}\right)}_{\displaystyle = \underline{u}_i}</math>. | \vec{u}_i = \left(\vec{e}_x,\vec{e}_y,\vec{e}_z\right)\cdot \underbrace{\left(\begin{array}{l}u_x\\u_y\\u_z\end{array}\right)}_{\displaystyle = \underline{u}_i}</math>. | ||
Dabei ist z.B. <i>i=1</i> und <i><math>\ell</math>=2,3</i>. | |||
Die drei Bewegungsgleichungen in den drei räumlichen Koordinaten <i><u>u</u><sub>i</sub></i> formulieren wir in dimensionslosen Koordinaten. Dafür brauchen wir drei unabhängige Referenzgrößen, hier wählen wir | |||
::<math> | ::<math> | ||
\begin{array}{lcll} | \begin{array}{lcll} | ||
M&=&m_1&\text{Referenz-Masse}\\ | M&=&m_1&\text{ Referenz-Masse}\\ | ||
L&=&1.6 10^{11} km&\text{Referenz-Länge: der Durchmesser unseres Sonnensystems}\\ | L&=&1.6 10^{11} \text{km}&\text{ Referenz-Länge: der Durchmesser unseres Sonnensystems und}\\ | ||
F&=& G\cdot \frac{\displaystyle m_1\cdot m_1}{\displaystyle L^2}& \text{Referenz-Kraft} | F&=& G\cdot \frac{\displaystyle m_1\cdot m_1}{\displaystyle L^2}& \text{Referenz-Kraft} | ||
\end{array} | \end{array}. | ||
</math> | </math> | ||
Und fehlt noch die Referent-Zeit <i>T</i>, die wir aus | |||
::<math> | ::<math> | ||
F = \frac{\displaystyle m_1\cdot L}{\displaystyle T^2} \text{ | F = \frac{\displaystyle m_1\cdot L}{\displaystyle T^2} \text{ zu } T = \sqrt{\frac{\displaystyle m_1\cdot L}{\displaystyle F}} | ||
</math> | </math> | ||
erhalten. | |||
Damit können wir schreiben: | |||
::<math> | ::<math> | ||
\begin{array}{lcll} | \begin{array}{lcll} | ||
t&=&\tau \cdot T&\text{ mit der dimensionslosen Zeit } \tau\\ | t&=&\tau \cdot T&\text{ mit der dimensionslosen Zeit } \tau\\ | ||
\underline{u}_i(t)&=&L\cdot \underline{U}_i(\tau)&\text{ mit den dimensionslose Koordinaten } U_i\\ | m_i&=&\theta_i \cdot m_1&\text{ mit der dimensionslosen Masse } \theta_i\\ | ||
\underline{u}_i(t)&=&L\cdot \underline{U}_i(\tau)&\text{ mit den dimensionslose Koordinaten } U_i \text{ und}\\ | |||
r_{i,j}&=& L \cdot \varrho_{i,j}&\text{ mit dem dimensionslosen Abstand zweier Körper } \varrho_{i,j} | r_{i,j}&=& L \cdot \varrho_{i,j}&\text{ mit dem dimensionslosen Abstand zweier Körper } \varrho_{i,j} | ||
\end{array} | \end{array}. | ||
</math> | </math> | ||
Einsetzen und Kürzen liefert uns dann die dimensionslosen Bewegungsgleichungen | |||
::<math> \ddot{\underline{U}}_i = \sum_{\ell=j,k} \frac{\displaystyle \theta_\ell}{\displaystyle varrho_{i,\ell}^2} \dot \underline{e}_{i,\ell} </math>. | |||
|code= | |||
<syntaxhighlight lang="matlab" line start=1> | |||
function dydt = t3bpdydt(t,y,sys) | |||
% implementation of ode | |||
% params hold system parameters | |||
% get coordinates | |||
for body = 1:3 | |||
u(body,1:3) = transpose(y(3*(body-1)+1:3*body,1)); | |||
end | |||
r = zeros(3,3,3); | |||
e = zeros(3,3,3); | |||
% compose vectors, unit vectors and distances | |||
r(1,2,:) = u(2,:)-u(1,:); % this from m[1] to m[2] | |||
R(1,2) = sqrt(sum(r(1,2,:).^2)); % magnitude of vector | |||
e(1,2,:) = r(1,2,:)/R(1,2); % unit vector length | |||
r(2,1,:) = -r(1,2,:); % .. and back | |||
e(2,1,:) = -e(1,2,:); | |||
R(2,1) = R(1,2); | |||
r(1,3,:) = u(3,:)-u(1,:); % this from m[1] to m[2] | |||
R(1,3) = sqrt(sum(r(1,3,:).^2)); | |||
e(1,2,:) = r(1,2,:)/R(1,2); % unit vector length | |||
r(3,1,:) = -r(1,3,:); % .. and back | |||
e(3,1,:) = -e(1,3,:); | |||
R(3,1) = R(1,3); | |||
r(2,3,:) = u(3,:)-u(2,:); % this from m[1] to m[2] | |||
R(2,3) = sqrt(sum(r(2,3,:).^2)); | |||
e(2,3,:) = r(2,3,:)/R(2,3); % unit vector length | |||
r(3,2,:) = -r(2,3,:); % .. and back | |||
e(3,2,:) = -e(2,3,:); | |||
R(3,2) = R(2,3); | |||
%% accelerations | |||
% mass 1 | |||
dydt(9+1:9+3,1)=sys.theta(2)/R(1,2)*e(1,2,:)+sys.theta(3)/R(1,3)*e(1,3,:); | |||
% mass 2 | |||
dydt(9+4:9+6,1)=sys.theta(1)/R(2,1)*e(2,1,:)+sys.theta(3)/R(2,3)*e(2,3,:); | |||
% mass 3 | |||
dydt(9+7:9+9,1)=sys.theta(1)/R(3,1)*e(3,1,:)+sys.theta(2)/R(3,2)*e(3,2,:); | |||
%% velocities | |||
dydt(1:9,1) = y(10:18,1); | |||
%% | |||
waitbar(t / sys.tEnd); | |||
end | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 82: | Zeile 129: | ||
|text=Text | |text=Text | ||
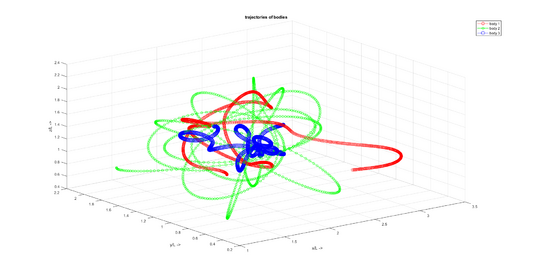
[[Datei:T3BP-21.png|550px|left|mini| | [[Datei:T3BP-21.png|550px|left|mini|Trajektoren der Körper]] | ||
[[Datei:T3BP-22.png|150px|left|mini| | [[Datei:T3BP-22.png|150px|left|mini|Bewegungsgrößen <i>Σ M<sub>i</sub> <i>I<sub>i,x</sub></i>]] | ||
[[Datei:T3BP-23.mp4|100%|left|mini| | [[Datei:T3BP-23.mp4|100%|left|mini|Animation der Bewegung]] | ||
|code= | |code= | ||
Version vom 2. Oktober 2022, 19:39 Uhr
Aufgabenstellung
Sie untersuchen das „Three-Body-Problem“(vgl. Wikipedia) numerisch. Dabei sollen die Bahnen von drei Körper mit den Punktmassen m1, m2, m3 in Wechselwirkung miteinander berechnet werden.
Gesucht ist die Lösung des Anfangswertproblems für verschiedene Anfangswerte (Orte und Geschwindigkeiten) und Massen mi der Körper.
Lösung mit Matlab®
Lorem Ipsum ....
tmp
Header
Text
1+1
Declarations
Text
1+1
Equilibrium Conditions
Die Bewegungsgleichungen schreiben wir in Vektorschreibweise für Körper i als
- .
Dabei ist z.B. i=1 und =2,3.
Die drei Bewegungsgleichungen in den drei räumlichen Koordinaten ui formulieren wir in dimensionslosen Koordinaten. Dafür brauchen wir drei unabhängige Referenzgrößen, hier wählen wir
Und fehlt noch die Referent-Zeit T, die wir aus
erhalten.
Damit können wir schreiben:
Einsetzen und Kürzen liefert uns dann die dimensionslosen Bewegungsgleichungen
- .
function dydt = t3bpdydt(t,y,sys)
% implementation of ode
% params hold system parameters
% get coordinates
for body = 1:3
u(body,1:3) = transpose(y(3*(body-1)+1:3*body,1));
end
r = zeros(3,3,3);
e = zeros(3,3,3);
% compose vectors, unit vectors and distances
r(1,2,:) = u(2,:)-u(1,:); % this from m[1] to m[2]
R(1,2) = sqrt(sum(r(1,2,:).^2)); % magnitude of vector
e(1,2,:) = r(1,2,:)/R(1,2); % unit vector length
r(2,1,:) = -r(1,2,:); % .. and back
e(2,1,:) = -e(1,2,:);
R(2,1) = R(1,2);
r(1,3,:) = u(3,:)-u(1,:); % this from m[1] to m[2]
R(1,3) = sqrt(sum(r(1,3,:).^2));
e(1,2,:) = r(1,2,:)/R(1,2); % unit vector length
r(3,1,:) = -r(1,3,:); % .. and back
e(3,1,:) = -e(1,3,:);
R(3,1) = R(1,3);
r(2,3,:) = u(3,:)-u(2,:); % this from m[1] to m[2]
R(2,3) = sqrt(sum(r(2,3,:).^2));
e(2,3,:) = r(2,3,:)/R(2,3); % unit vector length
r(3,2,:) = -r(2,3,:); % .. and back
e(3,2,:) = -e(2,3,:);
R(3,2) = R(2,3);
%% accelerations
% mass 1
dydt(9+1:9+3,1)=sys.theta(2)/R(1,2)*e(1,2,:)+sys.theta(3)/R(1,3)*e(1,3,:);
% mass 2
dydt(9+4:9+6,1)=sys.theta(1)/R(2,1)*e(2,1,:)+sys.theta(3)/R(2,3)*e(2,3,:);
% mass 3
dydt(9+7:9+9,1)=sys.theta(1)/R(3,1)*e(3,1,:)+sys.theta(2)/R(3,2)*e(3,2,:);
%% velocities
dydt(1:9,1) = y(10:18,1);
%%
waitbar(t / sys.tEnd);
end
Solving
Text
1+1
Post-Processing
Text

1+1
Links
- ...
Literature
- ...