Gelöste Aufgaben/T3BP: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
"Die Drei Sonnen"
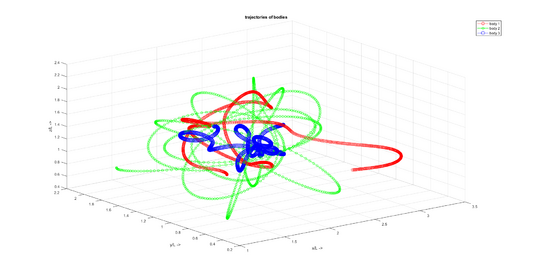
"Trajektoren der Körper" 
"Bewegungsgrößen Σ Mi Ii,x" "Animation der Bewegung"
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 41: | Zeile 41: | ||
::<math> | ::<math> | ||
\begin{array}{lcll} | \begin{array}{lcll} | ||
M&=&m_1&\text{ | M&=&m_1&\text{Referenz-Masse}\\ | ||
L&=&1.6 10^{11} km&\text{ | L&=&1.6 10^{11} km&\text{Referenz-Länge: der Durchmesser unseres Sonnensystems}\\ | ||
F&=& G\cdot \frac{\displaystyle m_1\cdot m_1}{\displaystyle L^2}& \text{ | F&=& G\cdot \frac{\displaystyle m_1\cdot m_1}{\displaystyle L^2}& \text{Referenz-Kraft} | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
::<math> | |||
F = \frac{\displaystyle m_1\cdot L}{\displaystyle T^2} \text{ und damit } T = \sqrt{\frac{\displaystyle m_1\cdot L}{\displaystyle F}} | |||
</math> | |||
::<math> | |||
\begin{array}{lcll} | |||
t&=&\tau \cdot T&\text{ mit der dimensionslosen Zeit } \tau\\ | |||
\underline{u}_i(t)&=&L\cdot \underline{U}_i(\tau)&\text{ mit den dimensionslose Koordinaten } U_i\\ | |||
r_{i,j}&=& L \dot \varrho_{i,j}&\text{ mit dem dimensionslosen Abstand zweier Körper } \varrho_{i,j} | |||
\end{array} | |||
</math> | |||
Version vom 2. Oktober 2022, 19:17 Uhr
Aufgabenstellung
Sie untersuchen das „Three-Body-Problem“(vgl. Wikipedia) numerisch. Dabei sollen die Bahnen von drei Körper mit den Punktmassen m1, m2, m3 in Wechselwirkung miteinander berechnet werden.

Gesucht ist die Lösung des Anfangswertproblems für verschiedene Anfangswerte (Orte und Geschwindigkeiten) und Massen mi der Körper.
Lösung mit Matlab®
Lorem Ipsum ....
tmp
Header
Text
1+1
Declarations
Text
1+1
Equilibrium Conditions
Text
1+1
Solving
Text
1+1
Post-Processing
Text


1+1
Links
- ...
Literature
- ...