Gelöste Aufgaben/Kitb: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Category:Gelöste Aufgaben Category:A*x=b Category:Numerische Lösung Category:Randwertproblem [[Category:Prinzip der virtuellen Verrückungen]…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Diese Aufgabe ist eine Variante der Aufgabe „[[Gelöste Aufgaben/Kita|Kita]]“, bei der die analytische Lösung gesucht ist. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:Kita-01.png|150px|left|mini|Lageplan]] | [[Datei:Kita-01.png|150px|left|mini|Lageplan]] | ||
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. | Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. | ||
Gesucht ist die | Gesucht ist die Näherungslösung für ein FE-Modell des Masts (Euler-Bernoulli-Balken) und der drei Dehnstäbe. | ||
</onlyinclude> | </onlyinclude> | ||
[[Datei:Kita-02.png|190px|right|mini|Sicht auf den Mast]] | [[Datei:Kita-02.png|190px|right|mini|Sicht auf den Mast]] | ||
| Zeile 26: | Zeile 27: | ||
Ein Knicken der drei Stäbe sei ausgeschlossen. | Ein Knicken der drei Stäbe sei ausgeschlossen. | ||
== Lösung mit Maxima == | ==Lösung mit Maxima== | ||
Mit Maxima berechnen wir die | Mit Maxima berechnen wir die Lösung des Problems mit der Methode der Finiten Elemente. | ||
Die | Da wir in Aufgabe „Kita“ bereits die Knoten-Variablen als Hilfsgrößen eingeführt haben, können wir die Nomenklatur, Parameter und abgeleitete Größen direkt übernehmen - und die Ergebnisse auch vergleichen. | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Kern der Lösung ist die Komposition der Element-Steifigkeitsmatrix sowie der "rechten Seite" des Gleichungssystems. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 21.05.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2022-08-19 */ | |||
/* ref: NMM, Labor 2 */ | |||
/* Mast unter linear-veränderlicher Windlast */ | |||
/* - Lösung mit der Methode der FE */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
Die Parameter können wir direkt aus Kita übernehmen. Hinzu kommt die Definition der Trial-Functions aus XXXX – die wir anstelle der allgemeinen Lösung der Differentialbeziehung für w(x), v(x) ansetzen. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* declarations */ | |||
/* *****************************************************/ | |||
/* parameter selection */ | |||
params: [[EA[2]=2*EA[1],EA[3]=EA[1], EA[1] = α*EI/R^2], [h[1] = 2*h[2], h[2]=sqrt(2)*R]]; | |||
assume(R>0); | |||
/* trial-functions */ | |||
φ : [ 2*ξ^3-3*ξ^2+1, | |||
(ξ^3-2*ξ^2+ξ)*ℓ[i], | |||
3*ξ^2-2*ξ^3, | |||
(ξ^3-ξ^2)*ℓ[i]]; | |||
/* non-sclar variables */ | |||
declare(r,nonscalar, | |||
e,nonscalar); | |||
/* geometry **********************************/ | |||
/* points */ | |||
geo: [r[H] = matrix([ h[1], 0, 0]), | |||
r[A] = matrix([ 0 , R*sin( 0 ),-R*cos( 0 )]), | |||
r[B] = matrix([ 0 , R*sin(-2*%pi/3),-R*cos(-2*%pi/3)]), | |||
r[C] = matrix([ 0 , R*sin(+2*%pi/3),-R*cos(+2*%pi/3)])]; | |||
geo: append(geo, subst(geo, [r[1] = r[A]-r[H], | |||
r[2] = r[B]-r[H], | |||
r[3] = r[C]-r[H]])); | |||
geo: append(geo, [L = sqrt(subst(geo,r[1]).subst(geo,r[1]))]); | |||
/* unit-vecotor coefficients */ | |||
geo: append(geo, makelist(e[i]=subst(geo,r[i]/L),i,1,3)); | |||
</syntaxhighlight> | |||
}} | |||
| Zeile 39: | Zeile 96: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Title | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Title | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<table class="wikitable mw-collapsible" style="background-color:white; float: left; margin-right:14px;"> | <table class="wikitable mw-collapsible" style="background-color:white; float: left; margin-right:14px;"> | ||
| Zeile 46: | Zeile 124: | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | *... | ||
'''Literature''' | '''Literature''' | ||
* ... | *... | ||
Version vom 15. September 2022, 16:04 Uhr
Aufgabenstellung
Diese Aufgabe ist eine Variante der Aufgabe „Kita“, bei der die analytische Lösung gesucht ist.
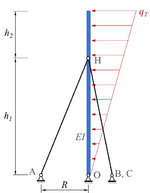
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird.
Gesucht ist die Näherungslösung für ein FE-Modell des Masts (Euler-Bernoulli-Balken) und der drei Dehnstäbe.
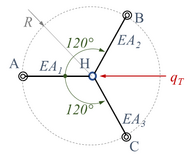
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „O“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „H“ mit dem Mast verbunden und in den Punkten „A“, „B“ und „C“ gelenkig gelagert. Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert qT und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt h1 = 2 h2, h2 = √2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A2=2 E A1,E A3=E A1.
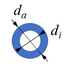
Der Mast hat ein zylindrisches Profil mit Innen- und Außendurchmesser di, da.
Ein Knicken der drei Stäbe sei ausgeschlossen.
Lösung mit Maxima
Mit Maxima berechnen wir die Lösung des Problems mit der Methode der Finiten Elemente. Da wir in Aufgabe „Kita“ bereits die Knoten-Variablen als Hilfsgrößen eingeführt haben, können wir die Nomenklatur, Parameter und abgeleitete Größen direkt übernehmen - und die Ergebnisse auch vergleichen.
Header
Kern der Lösung ist die Komposition der Element-Steifigkeitsmatrix sowie der "rechten Seite" des Gleichungssystems.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 21.05.2 */
/* author: Andreas Baumgart */
/* last updated: 2022-08-19 */
/* ref: NMM, Labor 2 */
/* Mast unter linear-veränderlicher Windlast */
/* - Lösung mit der Methode der FE */
/*******************************************************/
Declarations
Die Parameter können wir direkt aus Kita übernehmen. Hinzu kommt die Definition der Trial-Functions aus XXXX – die wir anstelle der allgemeinen Lösung der Differentialbeziehung für w(x), v(x) ansetzen.
/*******************************************************/
/* declarations */
/* *****************************************************/
/* parameter selection */
params: [[EA[2]=2*EA[1],EA[3]=EA[1], EA[1] = α*EI/R^2], [h[1] = 2*h[2], h[2]=sqrt(2)*R]];
assume(R>0);
/* trial-functions */
φ : [ 2*ξ^3-3*ξ^2+1,
(ξ^3-2*ξ^2+ξ)*ℓ[i],
3*ξ^2-2*ξ^3,
(ξ^3-ξ^2)*ℓ[i]];
/* non-sclar variables */
declare(r,nonscalar,
e,nonscalar);
/* geometry **********************************/
/* points */
geo: [r[H] = matrix([ h[1], 0, 0]),
r[A] = matrix([ 0 , R*sin( 0 ),-R*cos( 0 )]),
r[B] = matrix([ 0 , R*sin(-2*%pi/3),-R*cos(-2*%pi/3)]),
r[C] = matrix([ 0 , R*sin(+2*%pi/3),-R*cos(+2*%pi/3)])];
geo: append(geo, subst(geo, [r[1] = r[A]-r[H],
r[2] = r[B]-r[H],
r[3] = r[C]-r[H]]));
geo: append(geo, [L = sqrt(subst(geo,r[1]).subst(geo,r[1]))]);
/* unit-vecotor coefficients */
geo: append(geo, makelist(e[i]=subst(geo,r[i]/L),i,1,3));
Title
Text
1+1
Title
Text
1+1
Title
Text
1+1
Links
- ...
Literature
- ...