Gelöste Aufgaben/Kita

Aufgabenstellung

Lageplan

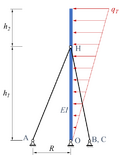
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird.

Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe.

Sicht auf den Mast

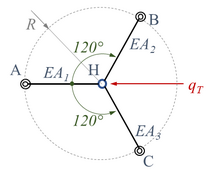
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „O“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „H“ mit dem Mast verbunden und in den Punkten „A“, „B“ und „C“ gelenkig gelagert. Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert q_T und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt h₁ = 2 h₂, h₂ = √2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A₂=2 E A₁,E A₃=E A₁.

Mastpril-Querschnitt

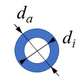
Der Mast hat ein zylindrisches Profil mit Innen- und Außendurchmesser d_i, d_a.

Ein Knicken der drei Stäbe sei ausgeschlossen.

Lösung mit Maxima

Mit Maxima berechnen wir die allgemeine Lösung der Differentialgleichung des Euler-Bernoulli-Balkens und geben die Rand- und Übergangsbedingungen an. Der Mast soll in Längsrichtung nicht signifikant durch die Stabkräfte verformt werden, als Koordinaten der Verschiebung haben hier also nur die Auslenkungen Querrichtung sowie die Verdrehungen um diese Koordinatenrichtungen. Die Stabkräfte berechnen wir aus der Längung der Stäbe, dabei linearisieren wir bezüglich der Mast-Auslenkungen.

Header

Kern der Lösung ist die Berechnung der Integrationskonstanten des Euler-Bernoulli-Balkens. In diesem Beispiel führen wir zusätzliche Konstanten ein, um die Rand- und Übergangsbedingungen einfacher formulieren zu können.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 21.05.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2022-08-19                            */
/* ref: NMM, Labor 1                                   */
/* Mast unter linear-veränderlicher Windlast           */
/*                                                     */
/*******************************************************/

Declarations

Wir übernehmen die Parameter aus der Aufgabenstellung, also

${\begin{array}{ccl}EA_{2}&=&2EA_{1},\\EA_{3}&=&EA_{1},\\h_{1}&=&2h_{2},\\h_{2}&=&{\sqrt {2*R}}{\text{ und }}\\EA_{1}&=&\alpha EI/R^{2}\end{array}}$

und definieren für die Berechnung der Stabkräfte die Referenzorte von A, B, C und H wie skizziert im x, y, z Koordinatensystem zu

${\underline {r}}_{H}={\begin{pmatrix}h_{1}\\0\\0\end{pmatrix}},{\underline {r}}_{A}=R{\begin{pmatrix}0\\\sin(0)\\-\cos(0\end{pmatrix}},{\underline {r}}_{B}=R{\begin{pmatrix}0\\\sin(-2\pi /3)\\-\cos(-2\pi /3)\end{pmatrix}},{\underline {r}}_{C}=R{\begin{pmatrix}0\\\sin(+2\pi /3)\\-\cos(+2\pi /3)\end{pmatrix}}.$

Die Koordinaten der Vektoren, die jeweils in Stablängsrichtung von H zu den Lagerpunkten zeigen, sind dann

${\underline {r}}_{1}={\underline {r}}_{A}-{\underline {r}}_{H},{\underline {r}}_{2}={\underline {r}}_{B}-{\underline {r}}_{H}und{\underline {r}}_{3}={\underline {r}}_{C}-{\underline {r}}_{H},$

die Referenz-Länge aller drei Stäbe ist damit

$L=||{\underline {r}}_{i}||,i=1,2{\text{ oder }}3$.

Und wir schreiben damit die Koordinaten der Einheitsvektoren dieser Stab-Längsrichtungen als

${\underline {e}}_{i}={\frac {\displaystyle {\underline {r}}_{i}}{\displaystyle L}},i=1,2,3$.

/*******************************************************/
/* declarations                                        */
/* *****************************************************/

/* parameter selection */
params: [EA[2]=2*EA[1],EA[3]=EA[1], h[1] = 2*h[2], h[2]=sqrt(2)*R, EA[1] = α*EI/R^2];
assume(R>0);
  
/* non-sclar variables */
declare(r,nonscalar,
        e,nonscalar);

/* geometry           **********************************/
/* points */
geo: [r[H] = matrix([ h[1], 0, 0]),
      r[A] = matrix([   0 , R*sin(    0   ),-R*cos(    0   )]),
      r[B] = matrix([   0 , R*sin(-2*%pi/3),-R*cos(-2*%pi/3)]),
      r[C] = matrix([   0 , R*sin(+2*%pi/3),-R*cos(+2*%pi/3)])];
geo: append(geo, subst(geo, [r[1] = r[A]-r[H],
                             r[2] = r[B]-r[H],
                             r[3] = r[C]-r[H]]));
geo: append(geo, [L = sqrt(subst(geo,r[1]).subst(geo,r[1]))]);
/* unit-vecotor coefficients */
geo: append(geo, makelist(e[i]=subst(geo,r[i]/L),i,1,3));

Integration Of Differential Equation for Euler-Bernoulli-Beam

In den Bereichen I und II haben wir jeweils eine Auslenkung des Masts in zwei Richtungen: z und y.

Wir nutzen die Standard-Nomenklatur für den Euler-Bernoulli-Balken und schrieben jeweils die Gleichgewichtsbedingungen

	... in z-Richtung als	... in y-Richtung als
	${\displaystyle E\,I\,w_{i}^{IV}(x)=q_{z},\;\;i=\{1,2\}}$.	${\displaystyle E\,I\,v_{i}^{IV}(x)=q_{y},\;\;i=\{1,2\}}$.
Für die Auslenkungen in z und y-Richtung geben wir hier die Bedeutung der Koordinaten vi(x), wi(x) je Bereich und deren Ableitungen an. Es ist
... die Querschnitts-Auslenkung:	$w_{i}(x)$	$v_{i}(x)$
... die Querschnitts-Verdrehung:	$\phi _{i}(x)={\frac {\displaystyle d\,w_{i}(x)}{\displaystyle d\,x}}$	$\psi _{i}(x)={\frac {\displaystyle d\,v_{i}(x)}{\displaystyle d\,x}}$
... das Biege-Moment:	$M_{y,i}(x)=-EI{\frac {\displaystyle d^{2}\,w_{i}(x)}{\displaystyle d\,x^{2}}}$	$M_{z,i}(x)={\color {red}+}EI{\frac {\displaystyle d^{2}\,v_{i}(x)}{\displaystyle d\,x^{2}}}$ und
... die Querkraft:	$Q_{z,i}(x)=-EI{\frac {\displaystyle d^{3}\,w_{i}(x)}{\displaystyle d\,x^{3}}}$	$Q_{y,i}(x)=-EI{\frac {\displaystyle d^{3}\,v_{i}(x)}{\displaystyle d\,x^{3}}}$

Für die Streckenlasten auf den Mast gilt je Bereich "i":

• ... in z-Richtung: $q_{z,i}(x)=q_{z,i-1}\cdot (1-{\frac {\displaystyle x_{i}}{\displaystyle h_{i}}})+q_{z,i}\cdot {\frac {\displaystyle x_{i}}{\displaystyle h_{i}}}$ und
• ... in y-Richtung: $q_{y,i}(x)=0$

wobei

${\begin{array}{ccl}q_{z,0}&=&0\\q_{z,1}&=&{\color {red}-}q_{T}\cdot {\frac {\displaystyle h_{1}}{\displaystyle h_{1}+h_{2}}}\\q_{z,2}&=&{\color {red}-}q_{T}\\\end{array}}$

Mit diesen Ansätzen erhalten wir aus der Integration der Differentialbeziehung für den Euler-Bernoulli-Balken diese generischen (weil mit Integrationskonstanten) Lösungen:

Richung ...	z	y
Bereich I	$w_{I}(x)=-{\frac {q_{T}x^{5}}{120\left({h_{2}}+{h_{1}}\right)EI}}+{c_{1}}{\frac {{x}^{3}}{6}}+{c_{2}}{\frac {{x}^{2}}{2}}+{c_{3}}\;x+{c_{4}}$	${\displaystyle }$
Bereich II	Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w_{II}(x)=-\frac{\frac{h_1 q_T \left( \frac{x^4}{24}-\frac{x^5}{120 h_2}\right) }{h_2+h_1}+\frac{q_T x^5}{120 h_2}{EI} +{c_9} \frac{{{x}^{3}}}{6}+{c_{10}} \frac{{{x}^{2}}}{2}+{c_{11}}\;x+{c_{12}}\]}	${\displaystyle }$

CODE

Forces in Supporting Rods

TEXT

CODE

Boundary- and Transition-Conditions

TEXT

... aus Rand T

CODE

Solving

TEXT

CODE

Post-Processing

TEXT

CODE

---

Links

• ...

Literature

• ...