Gelöste Aufgaben/Kita: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 13: | Zeile 13: | ||
[[Datei:Kita-01.png|120px|left|mini|Lageplan]] | [[Datei:Kita-01.png|120px|left|mini|Lageplan]] | ||
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. | Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird. | ||
Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe. | Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe. | ||
</onlyinclude> | </onlyinclude> | ||
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „''O''“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „''H''“ mit dem Mast verbunden und in den Punkten „''A''“, „''B''“ und „''C''“ gelenkig gelagert. | Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „''O''“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „''H''“ mit dem Mast verbunden und in den Punkten „''A''“, „''B''“ und „''C''“ gelenkig gelagert. | ||
Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert ''q<sub>T</sub>'' und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt h<sub>1</sub> = 2 h2, h2 = 2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A2=2 E A1,E A3=E A1. | Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert ''q<sub>T</sub>'' und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt <i>h<sub>1</sub> = 2 h2</i>, h2 = 2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A2=2 E A1,E A3=E A1. | ||
Ein Knicken der drei Stäbe sei ausgeschlossen. | Ein Knicken der drei Stäbe sei ausgeschlossen. | ||
Version vom 14. September 2022, 08:17 Uhr
Aufgabenstellung
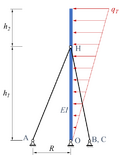
Das skizzierte System ist ein Mast unter einer linear veränderlichen Windlast, der durch drei gleichmäßig über den Umfang verteilten Stäbe abgestützt wird.
Gesucht ist die analytische Lösung für ein Euler-Bernoulli-Modell des elastischen Mastes und der drei Dehnstäbe.
Der Mast steht senkrecht dabei auf einer ebenen Unterlage mit dem festen Gelenklager „O“ und ist durch drei Stäbe abgestützt. Alle Stäbe sind in Punkt „H“ mit dem Mast verbunden und in den Punkten „A“, „B“ und „C“ gelenkig gelagert. Die Lager A, B und C sind gleichmäßig in einem Radius von R um O herum auf der Unterlage verteilt. Die Windlast hat den Maximalwert qT und wirkt in der Ebene, die durch die Punkte A, O und H aufgespannt werden. Für die Geometrie des Masts gilt h1 = 2 h2, h2 = 2 R, außerdem sei die Dehnsteifigkeiten der Stäbe E A2=2 E A1,E A3=E A1. Ein Knicken der drei Stäbe sei ausgeschlossen.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Title
Text
1+1
Links
- ...
Literature
- ...