Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode/FEM: Trial-Functions für kubische Ansatz-Polynome

Im Vergleich zu linearen Ansatzfunktionen brauchen wir oft Trial-Functions höherer Ordnung. So ist beim Euler-Bernoulli-Balken die virtuelle Formänderungsarbeit

$\delta \Pi =\displaystyle \int _{\ell }E\,I\;w''\cdot \delta w''dx$.

Zweimaliges Ableiten der linearen Trial-Funktion von oben führt dazu, dass die virtuelle Formänderungsarbeit komplett verschwindet - diese Ansatzfunktionen passen dann also nicht.

Ein Polynom zweiten Grades würde passen - hat aber nur drei Koeffizienten. Und eine ungerade Anzahl von Koeffizienten kann man nicht auf zwei Knoten gleich verteilen! Wie brauchen ein Polynom mit vier Koeffizienten.

Arbeitsschritte

Wir gehen die Arbeitsschritte zum Finden der Trial-Functions wie beim vorangehenden Schema durch:

• A→B Diskretisierung: Wir teilen die Struktur in N Stücke ( = Finite Elemente ) der Länge l_E. An jedem Ende eines Finiten Elements entsteht ein Knoten von insgesamt N+1 Knoten.
• B→C Trial-Funktion je Element:Je Element wählen wir ein kubisches Polynom (ein Polynom 3.ten Grades mit vier Koeffizienten) als Trial-Funktion

  ${\bar {w}}_{i}(x)=\left\{{\begin{array}{l}a_{i,3}\cdot x^{3}+a_{i,2}\cdot x^{2}+a_{i,1}\cdot x+a_{i,0}{\text{ im Element }}i\\0{\text{ sonst}}\end{array}}\right.$

  so dass wir als Approximation nun

  ${\tilde {w}}(x)=\displaystyle \sum _{4N}a_{n}\cdot \phi _{n}(x)$

  haben, mit den {a_i,3, a_i,2, a'_i,1 ,a_i,0} als gesuchte Wichtungsfaktoren.
• C→D Anpassen der Trial-Funktion an Übergangsbedingungen: Die 4N Koeffizienten {a_i,3, a_i,2, a'_i,1 ,a_i,0} können wir wiederum nicht anschaulich interpretieren. Mit der Koordinatentransformation auf die lokale Element-Koordinate ξ_i ist:

  ${\bar {w}}_{i}(\xi )=b_{i,3}\cdot \xi _{i}^{3}+b_{i,2}\cdot \xi _{i}^{2}+b_{i,1}\cdot \xi _{i}+b_{i,1}{\text{ mit }}x=x_{i}+\ell _{E}\cdot \xi _{i},\;\;x_{i}=(i-1)\cdot \ell _{E}$

  ξ_i ist nun die lokale, dimensionslose Ortskoordinate im Element. Für das kubische Polynom müssen wir nun noch sicherstellen, dass die Übergangsbedingungen zwischen den Elementen erfüllt sind. Das ist etwas komplizierter als bei der linearen Ansatzfunktion. Sie sehen, dass bei einem Balken nicht nur die Auslenkung der Elemente an den Übergangsknoten gleich sein muss - sondern auch der Kipp-Winkel Φ:

  

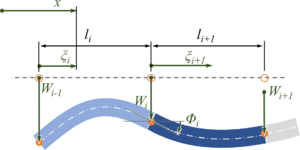
  Koordinaten des Stabes.

  Die Übergangsbedingungen sind also

  ${\bar {w}}_{i}(1)={\bar {w}}_{i+1}(0){\text{ und }}\underbrace {{\bar {w}}'_{i}(1)={\bar {w}}'_{i+1}(0)} _{\displaystyle {\text{mit }}w'=\Phi }$

  Das heißt: neben den Gleichgewichtsbedingungen müssen wir nun auch 2∙(N-1) algebraische Nebenbedingungen zwischen den b_i,3,  b_i,2,  b_i,1, b_i,0 erfüllen, damit an den Knoten die geometrischen Übergangsbedingungen erfüllt sind. Wieder ersetzen wir die b_ij durch die Knoten-Verschiebungen und Kipp-Winkel Φ des Balkens in den Knoten:

  ${\begin{array}{ll}w_{i}(0)&=W_{i-1}\\w'_{i}(0)&=\Phi _{i-1}\\w_{i}(1)&=W_{i}\\w'_{i}(1)&=\Phi _{i}\end{array}}$

  Trial Functions ϕ_i

  Durch Einsetzten unseres Polynoms in diese Randbedingungen können wir die vier generischen Koeffizienten bi,3,  bi,2,  bi,1, bi,0  gegen die Knoten-Koordinaten Wi-1, Φi-1, Wi, Φi tauschen und damit die Übergangsbedingungen implizit erfüllen! Wir finden

  ${\begin{array}{ll}{{b}_{i,3}}&=\left({{\Phi }_{i-1}}+{{\Phi }_{i}}\right)\cdot {{l}_{E}}-2\cdot {{W}_{i}}+2\cdot {{W}_{i-1}}\\{{b}_{i,2}}&=\left(-2\cdot {{\Phi }_{i-1}}-{{\Phi }_{i}}\right)\cdot {{l}_{E}}+3\cdot {{W}_{i}}-3\cdot {{W}_{i-1}}\\{{b}_{i,1}}&={{\Phi }_{i-1}}\cdot l_{E}\\{{b}_{i,0}}&={{W}_{i-1}}\end{array}}$

  und damit

  ${\begin{array}{ll}{\bar {w}}_{i}(x)&={{\xi }^{3}}\cdot \left(2\cdot {{W}_{i-1}}-2\cdot {{W}_{i}}+\left({{\Phi }_{i}}+{{\Phi }_{i-1}}\right)\cdot {{l}_{E}}\right)\\&+{{\xi }^{2}}\cdot \left(-3\cdot {{W}_{i-1}}+3\cdot {{W}_{i}}+\left(-{{\Phi }_{i}}-2\cdot {{\Phi }_{i-1}}\right)\cdot {{l}_{E}}\right)\\&+\xi \cdot {{\Phi }_{i-1}}\cdot {{l}_{E}}\\&+{{W}_{i-1}}\end{array}}$

  mit den 2(N+1) Koordinaten der Knoten-Verschiebungen Wn,Φn  als gesuchten Größen.

  
  

  /* Maxima */
  w(xi) := b[i,3]*xi^3+b[i,2]*xi^2+b[i,1]*xi+b[i,0];
  
  /* boundary conditions */
  BC: [w(0)=W[i-1],
       subst(0,xi,diff(w(xi),xi))/l[i] = Phi[i-1],
       w(1)=W[i],
       subst(1,xi,diff(w(xi),xi))/l[i] = Phi[i]];
  
  /* solve for polynom coeff. */
  sol: solve(BC,[b[i,3],b[i,2],b[i,1],b[i,0]])[1];
  print('w(xi),"=",subst(sol,w(xi)))$
  
  /* new coordinates = nodal displacements */
  Q : [W[i-1],Phi[i-1],W[i],Phi[i]];
  print('w(xi),"=",facsum(subst(sol,w(xi)),Q))$
  
  /* plot trial fcts */
  trials : expand(subst(sol,w(xi)));
  trials: makelist(coeff(trials,Q[j]), j,1,4);
  plot2d(subst([l[i]=5],trials),[xi,0,1], [xlabel, "ξ→"],
         [legend, "ϕ1", "ϕ2", "ϕ3", "ϕ4"],
         [style, [lines,3]] );

  
  

  
  

• D→E Einführung der Trial-Funktionen:Jetzt fehlt nur noch eine Kleinigkeit: wir sortieren die Gleichung für die Element-Verschiebung nach den Knoten-Variablen um und erhalten  

  ${\begin{array}{crc}{\bar {w}}_{i}(x)=&\;\;W_{i-1}\cdot &\underbrace {\left({{\left(\xi -1\right)}^{2}}\cdot \left(1+2\cdot \xi \right)\right)} _{\displaystyle =:\phi _{1}}\\&+\Phi _{i-1}\cdot &\underbrace {\left({{\left(\xi -1\right)}^{2}}\cdot \xi \cdot {{l}_{E}}\right)} _{\displaystyle =:\phi _{2}}\\&+W_{i}\cdot &\underbrace {\left({{\xi }^{2}}\cdot \left(3-2\cdot \xi \right)\right)} _{\displaystyle =:\phi _{3}}\\&+\Phi _{i}\cdot &\underbrace {\left(\left(\xi -1\right)\cdot {{\xi }^{2}}\cdot {{l}_{E}}\right)} _{\displaystyle =:\phi _{4}}\end{array}}$,

  so dass wir uns den Verschiebungsverlauf nun als Linearkombination der Funktionen ϕ₁, ϕ₂, ϕ₃ und ϕ₄ denken können. Die Form-Funktionen der Koordinaten sind hier für l_E=5 aufgetragen.

  

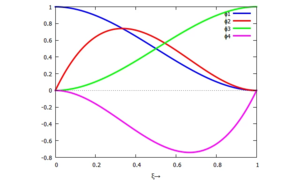
  Trial-Functions.

  Die virtuelle Formänderungs-Energie und die virtuelle Arbeit der d'Alembert'schen Trägheitskräfte je Euler-Bernoulli-Element für kubische Ansatz-Polynome

  Die gesamte virtuelle Formänderungsenergie δΠ und die virtuelle Arbeit der d'Alembert'schen Trägheitskräfte δW^a setzen wir jetzt aus aus den Formänderungsenergien je Element zusammen, also

  $\delta \Pi =\displaystyle \sum _{I}\delta \Pi _{i}$ und $\delta W^{a}=\displaystyle \sum _{I}\delta W_{i}^{a}$

  also für einen Euler-Bernoulli-Balken

  ${\begin{array}{lll}\delta \Pi _{i}&=+&\displaystyle \int _{\displaystyle \ell _{i}}E\,I\;w_{i}''\cdot \delta w_{i}''dx_{i}\\\delta W_{i}^{a}&=-&\displaystyle \int _{\displaystyle \ell _{i}}\varrho \,A\;{\ddot {w}}_{i}\cdot \delta w_{i}dx_{i}\end{array}}$

  Virtual Strain Energy

  Wir setzten also die Ansatzfunktionen von oben in dieses Integral ein und erhalten

  $\delta \Pi _{i}=\left({{\delta W}_{i-1}},{{\delta \Phi }_{i-1}},{{\delta W}_{i}},{{\delta \Phi }_{i}}\right)\cdot \displaystyle {\frac {EI}{{\ell }_{i}^{3}}}\cdot {\begin{pmatrix}12&6\cdot {{\ell }_{i}}&-12&6\cdot {{\ell }_{i}}\\6\cdot {{\ell }_{i}}&4\cdot {{\ell }_{i}^{2}}&-6\cdot {{\ell }_{i}}&2\cdot {{\ell }_{i}^{2}}\\-12&-6\cdot {{\ell }_{i}}&12&-6\cdot {{\ell }_{i}}\\6\cdot {{\ell }_{i}}&2\cdot {{\ell }_{i}^{2}}&-6\cdot {{\ell }_{i}}&4\cdot {{\ell }_{i}^{2}}\end{pmatrix}}\cdot {\begin{pmatrix}{{W}_{i-1}}\\{{\Phi }_{i-1}}\\{{W}_{i}}\\{{\Phi }_{i}}\end{pmatrix}}$

  Hier die Maxima-Kopiervorlage:

  phi : [ 2*xi^3-3*xi^2+1,
         (xi^3-2*xi^2+xi)*l[i],
          3*xi^2-2*xi^3,
         (xi^3-xi^2)*l[i]];
  Q[i] : [ W[i-1], Phi[i-1], W[i],Phi[i]];
  K[i] : EI[i]/l[i]^3 * matrix(
             [    12,   6*l[i],     -12,   6*l[i]],
             [6*l[i], 4*l[i]^2, -6*l[i], 2*l[i]^2],
             [   -12,  -6*l[i],      12,  -6*l[i]],
             [6*l[i], 2*l[i]^2, -6*l[i], 4*l[i]^2]);

  
  

  /* Maxima */
  
  /* trial-functions */
  ϕ : [2*ξ^3-3*ξ^2+1,
       ℓ*ξ^3-2*ℓ*ξ^2+ℓ*ξ,
       3*ξ^2-2*ξ^3,
       ℓ*ξ^3-ℓ*ξ^2];
  
  /* for element "i" */
   Q[i] : [ W[i-1](t), Φ[i-1](t), W[i](t), Φ[i](t)];
  δQ[i] : [δW[i-1]   ,δΦ[i-1]   ,δW[i]   ,δΦ[i]   ];
  
   w:  Q[i].φ;
  δw: δQ[i].φ;
  
  PvV : [δΠ[i] = 'integrate( EI*'diff(w,ξ,2)/ℓ^2*'diff(δw,ξ,2)/ℓ^2,ξ,0,1)*ℓ,
         δW[i] = 'integrate(  μ*'diff(w,t,2)*δw,ξ,0,1)*ℓ];
  PvV : expand(ev(PvV,nouns));
  K : funmake('matrix,
          makelist(
                makelist(
                     coeff(coeff(subst(PvV[1],δΠ[i]),δQ[i][row]),Q[i][col]),
                                        row,1,4),col,1,4));
  
  print(δΠ[i],"=", δQ[i],"*",EI/ℓ^3,"*",K/(EI/ℓ^3),"*",transpose(Q[i]))$

  
  

  
  

  
  

  Virtual Work of d'Alembert-Forces

  Wir setzten also auch hier die Ansatzfunktionen in das Integral für δW^a ein und erhalten mit $\mu =\varrho \,A$

  $\delta W_{i}^{a}=-\left({{\delta W}_{i-1}},{{\delta \Phi }_{i-1}},{{\delta W}_{i}},{{\delta \Phi }_{i}}\right)\cdot \displaystyle {\frac {\displaystyle {\varrho A\ell _{i}}}{\displaystyle 35}}\cdot {\begin{pmatrix}13&{\frac {11\ell _{i}}{6}}&{\frac {9}{2}}&-{\frac {13\ell _{i}}{12}}\\{\frac {11\ell _{i}}{6}}&{\frac {{\ell _{i}}^{2}}{3}}&{\frac {13\ell _{i}}{12}}&-{\frac {{\ell _{i}}^{2}}{4}}\\{\frac {9}{2}}&{\frac {13\ell _{i}}{12}}&13&-{\frac {11\ell _{i}}{6}}\\-{\frac {13\ell _{i}}{12}}&-{\frac {{\ell _{i}}^{2}}{4}}&-{\frac {11\ell _{i}}{6}}&{\frac {{\ell _{i}}^{2}}{3}}\end{pmatrix}}\cdot {\begin{pmatrix}{{\ddot {W}}_{i-1}}\\{{\ddot {\Phi }}_{i-1}}\\{{\ddot {W}}_{i}}\\{{\ddot {\Phi }}_{i}}\end{pmatrix}}$

  Hier die Maxima-Kopiervorlage:

  φϕ : [ 2*ξ^3-3*ξ^2+1,
         (ξ^3-2*ξ^2+ξ)*ℓ[i],
          3*ξ^2-2*ξ^3,
         (ξ^3-ξ^2)*ℓ[i]];
  Q[i] : [ W[i-1], Φ[i-1], W[i],Φ[i]];
  K[i] : EI[i]/ℓ[i]^3 * matrix(
             [    12,   6*ℓ[i],     -12,   6*ℓ[i]],
             [6*ℓ[i], 4*ℓ[i]^2, -6*ℓ[i], 2*ℓ[i]^2],
             [   -12,  -6*ℓ[i],      12,  -6*ℓ[i]],
             [6*ℓ[i], 2*ℓ[i]^2, -6*ℓ[i], 4*ℓ[i]^2]);

  
  

  /* Maxima */
  
  /* trial-functions */
  φ : [2*ξ^3-3*ξ^2+1,
       ℓ*ξ^3-2*ℓ*ξ^2+ℓ*ξ,
       3*ξ^2-2*ξ^3,
       ℓ*ξ^3-ℓ*ξ^2];
  
  /* for element "i" */
   Q[i] : [ W[i-1](t), Φ[i-1](t), W[i](t), Φ[i](t)];
  δQ[i] : [δW[i-1]   ,δΦ[i-1]   ,δW[i]   ,δΦ[i]   ];
  
   w:  Q[i].φ;
  δw: δQ[i].φ;
  
  PvV : [δΠ[i] = 'integrate( EI*'diff(w,ξ,2)/ℓ^2*'diff(δw,ξ,2)/ℓ^2,ξ,0,1)*ℓ,
         δW[i] = 'integrate(  μ*'diff(w,t,2)*δw,ξ,0,1)*ℓ];
  PvV : expand(ev(PvV,nouns));
  
  M : funmake('matrix,
          makelist(
                makelist(
                     coeff(coeff(subst(PvV[2],δW[i]),δQ[i][row]),diff(Q[i][col],t,2)),
                                        row,1,4),col,1,4));
  
  print(δW[i],"=", δQ[i],"*",μ*ℓ/35,"*",M/(μ*ℓ/35),"*",transpose(diff(Q[i],t,2)))$

  
  

  
  

  
  

  Links:

  • Im Vergleich: das Verfahren von Ritz und die Methode der Finite Elemente
  • FEM-Formulierung für den Euler-Bernoulli-Balken