Zeile 30:
Zeile 30: Dabei geben wir von einem Punkt ''P'' in Euler-Koordinaten mit
Dabei geben wir von einem Punkt ''P'' in Euler-Koordinaten mit
::<math></math>
::<math>
\begin{array}{l}\cos{\left( {{\theta }_3}\right) }=\frac{\sin{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } {{\cos{\left( {{\varphi }_3}\right) }}^{2}}-\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } {{\sin{\left( {{\theta }_3}\right) }}^{2}}}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\theta }_3}\right) }}\\
\begin{array}{l}\cos{\left( {{\theta }_3}\right) }=\frac{\sin{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } {{\cos{\left( {{\varphi }_3}\right) }}^{2}}-\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } {{\sin{\left( {{\theta }_3}\right) }}^{2}}}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\theta }_3}\right) }}\\
\sin{\left( {{\theta }_2}\right) }=-\frac{\sin{\left( {{\varphi }_1}\right) } \sin{\left( {{\theta }_3}\right) }}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) }}\\
\sin{\left( {{\theta }_2}\right) }=-\frac{\sin{\left( {{\varphi }_1}\right) } \sin{\left( {{\theta }_3}\right) }}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) }}\\
Zeile 37:
Zeile 37: \cos{\left( {{\theta }_1}\right) }=\cos{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) }\\
\cos{\left( {{\theta }_1}\right) }=\cos{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) }\\
{{\sin{\left( {{\theta }_3}\right) }}^{2}}=\frac{{{\sin{\left( {{\varphi }_2}\right) }}^{2}} {{\sin{\left( {{\varphi }_3}\right) }}^{2}}+2 \sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) } \sin{\left( {{\varphi }_3}\right) }+\left( 1-{{\cos{\left( {{\varphi }_1}\right) }}^{2}}\right) {{\cos{\left( {{\varphi }_2}\right) }}^{2}} {{\cos{\left( {{\varphi }_3}\right) }}^{2}}}{1-{{\cos{\left( {{\varphi }_1}\right) }}^{2}} {{\cos{\left( {{\varphi }_2}\right) }}^{2}}}\end{array}
{{\sin{\left( {{\theta }_3}\right) }}^{2}}=\frac{{{\sin{\left( {{\varphi }_2}\right) }}^{2}} {{\sin{\left( {{\varphi }_3}\right) }}^{2}}+2 \sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) } \sin{\left( {{\varphi }_3}\right) }+\left( 1-{{\cos{\left( {{\varphi }_1}\right) }}^{2}}\right) {{\cos{\left( {{\varphi }_2}\right) }}^{2}} {{\cos{\left( {{\varphi }_3}\right) }}^{2}}}{1-{{\cos{\left( {{\varphi }_1}\right) }}^{2}} {{\cos{\left( {{\varphi }_2}\right) }}^{2}}}\end{array}
</math>
::<math></math>
::<math></math>
Version vom 4. April 2022, 13:04 Uhr
Definition In Kugelkoordinaten oder räumlichen Polarkoordinaten wird ein Punkt P im dreidimensionalen Raum durch seinen Abstand vom Ursprung und zwei Winkel angegeben.
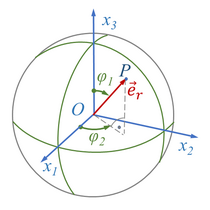
Kugelkoordinaten r, φ1 , φ2 eines Punktes P und kartesisches Koordinatensystem mit den Achsen x1 , x2 ,x3 . So ist der Vektor vom Ursprung zum Punkt P
r
→
=
r
⋅
e
→
r
{\displaystyle {\vec {r}}=r\cdot {\vec {e}}_{r}}
mit
e
→
r
=
(
sin
(
φ
1
)
cos
(
φ
2
)
sin
(
φ
1
)
sin
(
φ
2
)
cos
(
φ
1
)
)
{\displaystyle {\vec {e}}_{r}=\left({\begin{array}{c}\sin(\varphi _{1})\cos(\varphi _{2})\\\sin(\varphi _{1})\sin(\varphi _{2})\\\cos(\varphi _{1})\end{array}}\right)}
Die Kugelkoordinaten kann man - ähnlich wie bei den Euler-Winkeln -zur Definition eines neuen, lokalen Koordinatensystems nutzen.
Neben dem Flächen-Normalenvektor
e
→
r
{\displaystyle {\vec {e}}_{r}}
e
→
φ
,
1
,
e
→
φ
,
2
{\displaystyle {\vec {e}}_{\varphi ,1},{\vec {e}}_{\varphi ,2}}
φ1 und φ2 eine neue Basis
e
_
→
K
{\displaystyle {\vec {\underline {e}}}_{K}}
Einheitsvektoren der Orthogonalbasis
e
_
→
K
=
[
e
→
φ
,
1
,
e
→
φ
,
2
,
e
→
r
]
{\displaystyle {\vec {\underline {e}}}_{K}=\left[{\vec {e}}_{\varphi ,1},{\vec {e}}_{\varphi ,2},{\vec {e}}_{r}\right]}
P der Kugel mit
e
→
r
{\displaystyle {\vec {e}}_{r}}
e
→
φ
,
1
,
e
→
φ
,
2
{\displaystyle {\vec {e}}_{\varphi ,1},{\vec {e}}_{\varphi ,2}}
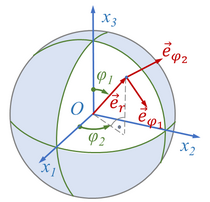
Die Koordinatentransformation erfolgt über
(
e
→
φ
,
1
e
→
φ
,
2
e
→
r
)
=
D
_
_
12
(
φ
1
(
t
)
,
φ
2
(
t
)
)
(
e
→
x
,
1
e
→
x
,
2
e
→
x
,
3
)
{\displaystyle \left({\begin{array}{c}{\vec {e}}_{\varphi ,1}\\{\vec {e}}_{\varphi ,2}\\{\vec {e}}_{r}\end{array}}\right)={\underline {\underline {D}}}_{12}\left(\varphi _{1}(t),\varphi _{2}(t)\right)\left({\begin{array}{c}{\vec {e}}_{x,1}\\{\vec {e}}_{x,2}\\{\vec {e}}_{x,3}\end{array}}\right)}
mit der Transformationsmatrix
D
_
_
12
(
φ
1
(
t
)
,
φ
2
(
t
)
)
=
(
cos
(
φ
1
(
t
)
)
cos
(
φ
2
(
t
)
)
cos
(
φ
1
(
t
)
)
sin
(
φ
2
(
t
)
)
−
sin
(
φ
1
(
t
)
)
−
sin
(
φ
2
(
t
)
)
cos
(
φ
2
(
t
)
)
0
sin
(
φ
1
(
t
)
)
cos
(
φ
2
(
t
)
)
sin
(
φ
1
(
t
)
)
sin
(
φ
2
(
t
)
)
cos
(
φ
1
(
t
)
)
)
{\displaystyle {\underline {\underline {D}}}_{12}\left(\varphi _{1}(t),\varphi _{2}(t)\right)={\begin{pmatrix}\cos {\left({{\varphi }_{1}}(t)\right)}\cos {\left({{\varphi }_{2}}(t)\right)}&\cos {\left({{\varphi }_{1}}(t)\right)}\sin {\left({{\varphi }_{2}}(t)\right)}&-\sin {\left({{\varphi }_{1}}(t)\right)}\\-\sin {\left({{\varphi }_{2}}(t)\right)}&\cos {\left({{\varphi }_{2}}(t)\right)}&0\\\sin {\left({{\varphi }_{1}}(t)\right)}\cos {\left({{\varphi }_{2}}(t)\right)}&\sin {\left({{\varphi }_{1}}(t)\right)}\sin {\left({{\varphi }_{2}}(t)\right)}&\cos {\left({{\varphi }_{1}}(t)\right)}\end{pmatrix}}}
Transformation von Euler-Winkeln Oft kann man räumliche Polarkoordinaten besser interpretieren als Euler-Winkel. Wir schreiben deshalb hier eine Transformationsvorschrift an, mit der Euler-Winkel in Polarkoordinaten übersetzten kann.
Dabei geben wir von einem Punkt P in Euler-Koordinaten mit
cos
(
θ
3
)
=
sin
(
φ
2
)
cos
(
φ
3
)
sin
(
φ
3
)
+
sin
(
φ
1
)
cos
(
φ
2
)
cos
(
φ
3
)
2
−
sin
(
φ
1
)
cos
(
φ
2
)
sin
(
θ
3
)
2
sin
(
φ
2
)
sin
(
θ
3
)
sin
(
θ
2
)
=
−
sin
(
φ
1
)
sin
(
θ
3
)
sin
(
φ
2
)
sin
(
φ
3
)
+
sin
(
φ
1
)
cos
(
φ
2
)
cos
(
φ
3
)
cos
(
θ
2
)
=
cos
(
φ
1
)
sin
(
φ
2
)
sin
(
θ
3
)
sin
(
φ
2
)
sin
(
φ
3
)
+
sin
(
φ
1
)
cos
(
φ
2
)
cos
(
φ
3
)
sin
(
θ
1
)
=
sin
(
φ
2
)
sin
(
φ
3
)
+
sin
(
φ
1
)
cos
(
φ
2
)
cos
(
φ
3
)
sin
(
θ
3
)
cos
(
θ
1
)
=
cos
(
φ
1
)
cos
(
φ
2
)
sin
(
θ
3
)
2
=
sin
(
φ
2
)
2
sin
(
φ
3
)
2
+
2
sin
(
φ
1
)
cos
(
φ
2
)
sin
(
φ
2
)
cos
(
φ
3
)
sin
(
φ
3
)
+
(
1
−
cos
(
φ
1
)
2
)
cos
(
φ
2
)
2
cos
(
φ
3
)
2
1
−
cos
(
φ
1
)
2
cos
(
φ
2
)
2
{\displaystyle {\begin{array}{l}\cos {\left({{\theta }_{3}}\right)}={\frac {\sin {\left({{\varphi }_{2}}\right)}\cos {\left({{\varphi }_{3}}\right)}\sin {\left({{\varphi }_{3}}\right)}+\sin {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}{{\cos {\left({{\varphi }_{3}}\right)}}^{2}}-\sin {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}{{\sin {\left({{\theta }_{3}}\right)}}^{2}}}{\sin {\left({{\varphi }_{2}}\right)}\sin {\left({{\theta }_{3}}\right)}}}\\\sin {\left({{\theta }_{2}}\right)}=-{\frac {\sin {\left({{\varphi }_{1}}\right)}\sin {\left({{\theta }_{3}}\right)}}{\sin {\left({{\varphi }_{2}}\right)}\sin {\left({{\varphi }_{3}}\right)}+\sin {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}\cos {\left({{\varphi }_{3}}\right)}}}\\\cos {\left({{\theta }_{2}}\right)}={\frac {\cos {\left({{\varphi }_{1}}\right)}\sin {\left({{\varphi }_{2}}\right)}\sin {\left({{\theta }_{3}}\right)}}{\sin {\left({{\varphi }_{2}}\right)}\sin {\left({{\varphi }_{3}}\right)}+\sin {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}\cos {\left({{\varphi }_{3}}\right)}}}\\\sin {\left({{\theta }_{1}}\right)}={\frac {\sin {\left({{\varphi }_{2}}\right)}\sin {\left({{\varphi }_{3}}\right)}+\sin {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}\cos {\left({{\varphi }_{3}}\right)}}{\sin {\left({{\theta }_{3}}\right)}}}\\\cos {\left({{\theta }_{1}}\right)}=\cos {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}\\{{\sin {\left({{\theta }_{3}}\right)}}^{2}}={\frac {{{\sin {\left({{\varphi }_{2}}\right)}}^{2}}{{\sin {\left({{\varphi }_{3}}\right)}}^{2}}+2\sin {\left({{\varphi }_{1}}\right)}\cos {\left({{\varphi }_{2}}\right)}\sin {\left({{\varphi }_{2}}\right)}\cos {\left({{\varphi }_{3}}\right)}\sin {\left({{\varphi }_{3}}\right)}+\left(1-{{\cos {\left({{\varphi }_{1}}\right)}}^{2}}\right){{\cos {\left({{\varphi }_{2}}\right)}}^{2}}{{\cos {\left({{\varphi }_{3}}\right)}}^{2}}}{1-{{\cos {\left({{\varphi }_{1}}\right)}}^{2}}{{\cos {\left({{\varphi }_{2}}\right)}}^{2}}}}\end{array}}}
{\displaystyle }
Links
Kugelkoordinaten auf Wikipedia Sources/Lexikon/Eulersche Winkel Quaternionen für Drehungen Geographische Koordinaten Literature
![{\displaystyle {\vec {\underline {e}}}_{K}=\left[{\vec {e}}_{\varphi ,1},{\vec {e}}_{\varphi ,2},{\vec {e}}_{r}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fe4b620c3267b60b67ff1f2c2989fc9fbf27702)
