Sources/Lexikon/Kugelkoordinaten: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 4: | Zeile 4: | ||
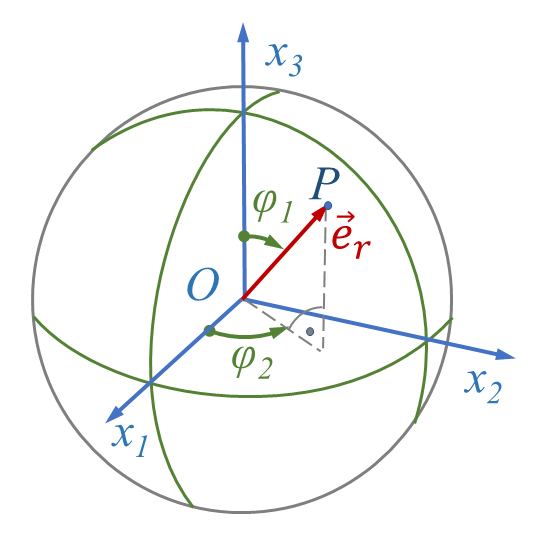
[[Datei:Kugelkoordinaten-01.png|gerahmt|links|Kugelkoordinaten r, φ<sub>1<sub> | [[Datei:Kugelkoordinaten-01.png|gerahmt|links|Kugelkoordinaten r, φ<sub>1</sub>, φ<sub>2</sub> eines Punktes ''P'' und kartesisches Koordinatensystem mit den Achsen x<sub>1</sub>, x<sub>2</sub>,x<sub>3</sub>.]] | ||
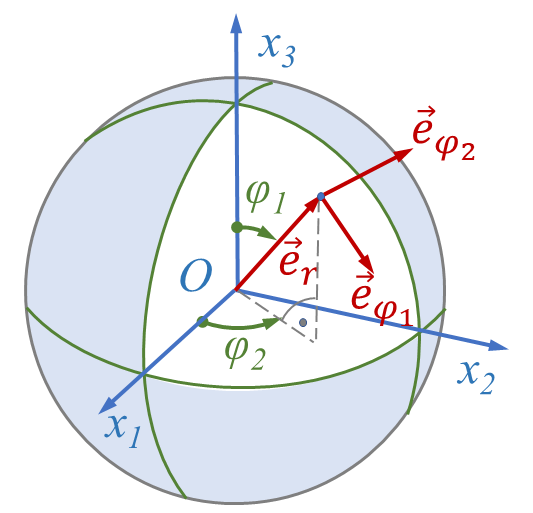
[[Datei:Kugelkoordinaten-02.png|gerahmt|rechts|Einheitsvektoren der Orthogonalbasis <math>\vec{\underline{e}}_K = \left[\vec{e}_r, \vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}\right]</math>, die in Punkt ''P'' der Kugel mit <math>\vec{e}_r</math> die Flächennormale definieren und mit <math>\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}</math> die Tangentialebene aufspannen.]] | [[Datei:Kugelkoordinaten-02.png|gerahmt|rechts|Einheitsvektoren der Orthogonalbasis <math>\vec{\underline{e}}_K = \left[\vec{e}_r, \vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}\right]</math>, die in Punkt ''P'' der Kugel mit <math>\vec{e}_r</math> die Flächennormale definieren und mit <math>\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}</math> die Tangentialebene aufspannen.]] | ||