Sources/Lexikon/Quaternionen für Drehungen: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
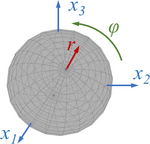
3D visualization einer Rotation bzgl. der Euler-Axe um den Winkel ϕ.
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Einheits-Quaternionen sind ein probates Werkzeug, um die räumliche Orientierung von Körpern zu beschreiben und räumliche Drehungen durchzuführen. | Einheits-Quaternionen sind ein probates Werkzeug, um die räumliche Orientierung von Körpern zu beschreiben und räumliche Drehungen durchzuführen. | ||
[[Datei:GYRQ-03.png|150px|mini|3D visualization einer Rotation | [[Datei:GYRQ-03.png|150px|mini|3D visualization einer Rotation bzgl. der Euler-Axe <math>\displaystyle \vec {r}</math> um den Winkel ϕ.]] | ||
Dabei wird die Rotation durch einen Drehwinkel ϕ um eine Rotationsachse | |||
::<math>\displaystyle \vec {r} = r_x \vec {e}_x + r_y \vec {e}_y + r_z \vec {e}_z</math> | |||
beschreiben. | |||
Bei Einheits-Quaternionen gilt | |||
::<math>\displaystyle \sqrt{r_x^2 + r_y^2 + r_z^2} = 1</math> | |||
Version vom 3. April 2022, 15:36 Uhr
Einheits-Quaternionen sind ein probates Werkzeug, um die räumliche Orientierung von Körpern zu beschreiben und räumliche Drehungen durchzuführen.

Dabei wird die Rotation durch einen Drehwinkel ϕ um eine Rotationsachse
beschreiben. Bei Einheits-Quaternionen gilt