Gelöste Aufgaben/GYRO: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 10: | Zeile 10: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Kreisel und Ihre Bewegungsgleichungen sind immer eine Herausforderung für Ingenieure. Hier nähern wir uns dem Thema mit dem Aufstellen und Lösen der Bewegungsgleichungen für große Winkel - und damit nichtlinearen Differentialgleichungen. | Kreisel und Ihre Bewegungsgleichungen sind immer wieder eine Herausforderung für Ingenieure. Hier nähern wir uns hier dem Thema mit dem Aufstellen und Lösen der Bewegungsgleichungen für große Winkel - und damit nichtlinearen Differentialgleichungen. | ||
<onlyinclude> | <onlyinclude> | ||
| Zeile 16: | Zeile 16: | ||
Gesucht ist die Präzessions-Bahn der eines Kreisels. | Gesucht ist die Präzessions-Bahn der eines Kreisels. | ||
Unser Kreisel ist ein Kegel der Höhe H und Radius R. | Unser Kreisel ist ein Kegel der Höhe H und Radius R. | ||
Die Bewegungsgleichungen sollen mit dem [Prinzip der virtuellen Verrückungen] aufgestellt werden. | Die Bewegungsgleichungen sollen mit dem [Prinzip der virtuellen Verrückungen] aufgestellt werden. Wir suchen nach der Trajektorie des Mittelpunktes des Kreisels für große Kippwinkel. | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Matlab<sup>®</sup> == | == Lösung mit Maxima und Matlab<sup>®</sup> == | ||
Wir arbeiten mit Maxima und Matlab. | |||
Maxima brauchen wir zum Aufstellen der Bewegungsgleichungen, die zunächst mal sehr komplex aussehen. Dabei linearisieren wir nicht oder gehen von einer Kreiselrotation mit konstanter Geschwindigkeit aus. Für die Lösung als [Anfangswertproblem] ist das | |||
{{MyCodeBlock|title=Header| | {{MyCodeBlock|title=Header| | ||
| Zeile 40: | Zeile 42: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Declarations | ||
|text= | |text=Wir brauchen | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
Version vom 28. März 2022, 20:49 Uhr
Aufgabenstellung
Kreisel und Ihre Bewegungsgleichungen sind immer wieder eine Herausforderung für Ingenieure. Hier nähern wir uns hier dem Thema mit dem Aufstellen und Lösen der Bewegungsgleichungen für große Winkel - und damit nichtlinearen Differentialgleichungen.
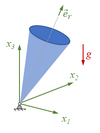
Gesucht ist die Präzessions-Bahn der eines Kreisels. Unser Kreisel ist ein Kegel der Höhe H und Radius R. Die Bewegungsgleichungen sollen mit dem [Prinzip der virtuellen Verrückungen] aufgestellt werden. Wir suchen nach der Trajektorie des Mittelpunktes des Kreisels für große Kippwinkel.
Lösung mit Maxima und Matlab®
Wir arbeiten mit Maxima und Matlab.
Maxima brauchen wir zum Aufstellen der Bewegungsgleichungen, die zunächst mal sehr komplex aussehen. Dabei linearisieren wir nicht oder gehen von einer Kreiselrotation mit konstanter Geschwindigkeit aus. Für die Lösung als [Anfangswertproblem] ist das
Header
Wir lösen hier das Anfangswertproblem zu nichtlinearen Bewegungsgleichungen.
Diese Gleichungen haben wir nicht - wir entwickeln sie ad-hoc und achten nur darauf, zentrale Phänomene abzubilden. Eine Abbildung der realen Zahlen ist nicht beabsichtigt.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 21.05.2 */
/* author: Andreas Baumgart */
/* last updated: 2022-03-27 */
/* ref: gyroscopic precession */
/* description: solve using principle of virt. work */
/*******************************************************/
Declarations
Wir brauchen
1+1
Links
- ...
Literature
- ...