Sources/Lexikon/Koordinaten

Wir unterscheiden

• unabhängige Koordinaten und
• abhängige Koordinaten.

Unabhängige Koordinaten identifizieren einen festen Punkt im Raum, z.B. den Punkt P: [x,y,z] in einer elastischen Struktur in seiner Referenzlage oder Punkt P: [x,y,z] in einem Strömungskanal.

Hier in der Struktur-Mechanik erfassen abhängige Koordinaten die Verschiebung eines Punktes, z.B. die Verschiebungen (u,v,w) des Punktes P aus seiner Referenzlage in seine ausgelenkte Lage. Jeder Massepunkt der Struktur hat eine individuelle Verschiebung, so dass u=u(x,y,z),  v=v(x,y,z),  w=w(x,y,z) - also die Verschiebungen abhängig vom Ursprungspunkt sind. Diese abhängigen Koordinaten heißen "materielle Koordinaten".

In der Strömungsmechanik sind die abhängigen Koordinaten nicht mit einzelnen Massepunkten verknüpft, sondern erfassen einen Zustand in einem räumlichen Punkt. Diese abhängigen Koordinaten heißen "räumliche Koordinaten".

Auch Punktmassen in Bewegung erfassen wir durch Verschiebungen (abhängige Koordinaten), hier u=u(t),  v=v(t),  w=w(t) .

Den Zusammenhang zwischen unabhängigen und abhängigen Koordinaten zeigt der Flug eines Federballs.

Flugbahn des Shuttlecocks

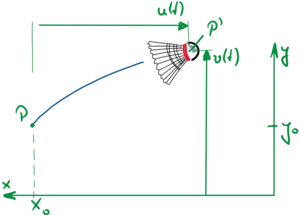
Die Bewegung vom Abflugpunkt P: [x₀,y₀] mit den unabhängigen Koordinaten x₀,y₀ zum Punkt P'  wird durch die abhängigen Koordinaten u(t), v(t) erfasst.