Sources/Lexikon/Virtuelle Arbeit von d'Alembert'schen Trägheitskräften: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „ölkölkö“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
== Das D'Alembert'sche Prinzip == | |||
Wenn Körper Drehungen um einen bewegten Drehpunkt ausführen oder Translationen in einem beschleunigten Koordinatensystem, wird die Arbeit mit dem Impuls- oder Momentensatz unpraktisch (vgl. [[Gelöste Aufgaben/Kw30|Kw30]]). | |||
[[Datei:VirtuelleArbeitvonTrägheitskräften.png|mini|150x150px|Kräfte an einer bewegten Punktemasse nach dem D'Alembertschen Prinzip]] | |||
Als Lösung schlägt 1743 d' Alembert [[Sources/Literatur#Szabo1977|[Szabo 1977]]] vor, Trägheitskräfte als äußere, eingeprägte Kräfte zu berücksichtigen. Wir stellen uns dabei vor, dass wie die Masse aus der Struktur herausschälen - es bleibt nur noch die leere Hülle des Körpers. | |||
Das Kräfte-Gleichgewicht mit dem Prinzip von d'Alembert lautet dann | |||
::<math>- m \; \ddot{\vec{r}} + \vec{K} = \vec{0}</math> | |||
== Die Lagrangesche Fassung des d' Alembertschen Prinzips == | |||
[https://de.wikipedia.org/wiki/Joseph-Louis_Lagrange Lagrange] integrierte 1788 dieses Prinzip in seine "[https://de.wikipedia.org/wiki/Lagrange-Formalismus Méchanique Analytique]" und bringt es so in seine heute gebräuchliche Form. | |||
Die Kräfte nach d'Alembert werden dabei als äußere, eingeprägte Kräfte berücksichtigt, die virtuelle Arbeit ihrer Kräfte für eine Punktmasse ist dann | |||
::<math>\displaystyle \delta W^a = (- m\;\ddot{\vec{r}} )\cdot \delta\vec{r}</math> | |||
Dies ist allerdings nur der Sonderfall des Prinzips für eine Punktmasse. Allgemeiner ist die Sichtweise für einen differentiellen Massepunkt ''ρ dV'' | |||
::<math>\displaystyle \delta W^a = \int_V (- \rho\;\ddot{\vec{r}} )\cdot \delta\vec{r} \;\;\;dV</math>. | |||
Aktuelle Version vom 21. April 2021, 15:47 Uhr
Das D'Alembert'sche Prinzip
Wenn Körper Drehungen um einen bewegten Drehpunkt ausführen oder Translationen in einem beschleunigten Koordinatensystem, wird die Arbeit mit dem Impuls- oder Momentensatz unpraktisch (vgl. Kw30).
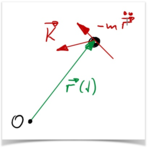
Als Lösung schlägt 1743 d' Alembert [Szabo 1977] vor, Trägheitskräfte als äußere, eingeprägte Kräfte zu berücksichtigen. Wir stellen uns dabei vor, dass wie die Masse aus der Struktur herausschälen - es bleibt nur noch die leere Hülle des Körpers.
Das Kräfte-Gleichgewicht mit dem Prinzip von d'Alembert lautet dann
Die Lagrangesche Fassung des d' Alembertschen Prinzips
Lagrange integrierte 1788 dieses Prinzip in seine "Méchanique Analytique" und bringt es so in seine heute gebräuchliche Form.
Die Kräfte nach d'Alembert werden dabei als äußere, eingeprägte Kräfte berücksichtigt, die virtuelle Arbeit ihrer Kräfte für eine Punktmasse ist dann
Dies ist allerdings nur der Sonderfall des Prinzips für eine Punktmasse. Allgemeiner ist die Sichtweise für einen differentiellen Massepunkt ρ dV
- .