Sources/Lexikon/Stab: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „k“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Unter einem Stab verstehen wir einen Körper, dessen Länge groß ist gegenüber seinen Querschnitts-Abmessungen. | |||
In der Mechanik nutzen wir dieses Längen-Verhältnis, um vereinfachte Modelle für bestimmte Belastungsarten abzuleiten. | |||
So heißen Stäbe, | |||
* Dehn-Stab, wenn sie durch eine Längs-Kraft belastetet werden, | |||
* Torsions-Stab, wenn sie durch eine Torsions-Moment belastetet werden und | |||
* Balken, wenn Sie durch ein Biegemoment und Querkraft belastet werden. | |||
[[Datei:Stab-01.png|mini|Stab-Theorie]] | |||
Gemeinsam ist diesen Modellen, dass sie die Verschiebung der materiellen Punkte eines Querschnitts nur durch eine unabhängige Koordinate "''x''" beschreiben können. | |||
Stab-Modell mit der unabhängigen Ortskoordinate "''x''". | |||
So können wir die Auslenkung eines materiellen Punktes in x-Richtung schreiben als | |||
<math>u(x,y,z) = U(x)+ z \cdot \Phi_y(x) + y \cdot \Phi_z(x) + y^2 \cdot \Psi_{zz}(x)+ y \cdot z \cdot \Psi_{yz}(x)+ z^2 \cdot\Psi_{yy}(x)+\ldots</math> | |||
mit den Querschnitts-Koordinaten | |||
<math>U(x), \Phi_y(x), \Phi_z(x), \Psi_{yy}(x), \Psi_{yz}(x), \Psi_{zz}(x)</math> | |||
für die wir jeweils Bewegungsgleichungen brauchen. | |||
Zu den einfachsten Stab-Modellen gehören | |||
* der [[Sources/Lexikon/Dehnstab|Dehnstab]] | |||
* der [[Sources/Lexikon/Torsionsstab|Torsionsstab]] | |||
* der [[Sources/Lexikon/Biegebalken|Biegebalken]] | |||
Von besonderem Interesse sind hier Balken-Modell, davon das einfachste: der [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]]. | |||
Aktuelle Version vom 21. April 2021, 15:08 Uhr
Unter einem Stab verstehen wir einen Körper, dessen Länge groß ist gegenüber seinen Querschnitts-Abmessungen.
In der Mechanik nutzen wir dieses Längen-Verhältnis, um vereinfachte Modelle für bestimmte Belastungsarten abzuleiten.
So heißen Stäbe,
- Dehn-Stab, wenn sie durch eine Längs-Kraft belastetet werden,
- Torsions-Stab, wenn sie durch eine Torsions-Moment belastetet werden und
- Balken, wenn Sie durch ein Biegemoment und Querkraft belastet werden.
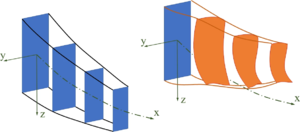
Gemeinsam ist diesen Modellen, dass sie die Verschiebung der materiellen Punkte eines Querschnitts nur durch eine unabhängige Koordinate "x" beschreiben können.
Stab-Modell mit der unabhängigen Ortskoordinate "x".
So können wir die Auslenkung eines materiellen Punktes in x-Richtung schreiben als
mit den Querschnitts-Koordinaten
für die wir jeweils Bewegungsgleichungen brauchen.
Zu den einfachsten Stab-Modellen gehören
- der Dehnstab
- der Torsionsstab
- der Biegebalken
Von besonderem Interesse sind hier Balken-Modell, davon das einfachste: der Euler-Bernoulli-Balken.