Sources/Lexikon/Schale: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 3: | Zeile 3: | ||
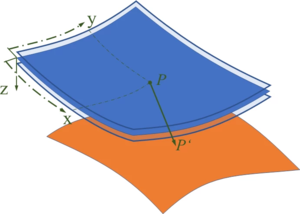
Unter einer Schale verstehen wir einen Körper, dessen Dicke sehr klein ist gegenüber seinen anderen Abmessungen. Alle Verschiebungen und Schnittlasten der Schale werden auf eine ''x''-''y''-Referenzebene bezogen - wie beim [[Sources/Lexikon/Stab|Stab]] auf die Referenzachse ''x''. Die Koordinaten der Schale sind demnach | Unter einer Schale verstehen wir einen Körper, dessen Dicke sehr klein ist gegenüber seinen anderen Abmessungen. Alle Verschiebungen und Schnittlasten der Schale werden auf eine ''x''-''y''-Referenzebene bezogen - wie beim [[Sources/Lexikon/Stab|Stab]] auf die Referenzachse ''x''. Die Koordinaten der Schale sind demnach | ||
<math>\underline{r}(x,y) = \left(\begin{array}{l} u(x,y)\\v(x,y)\\w(x,y) \end{array}\right)</math>. | ::<math>\underline{r}(x,y) = \left(\begin{array}{l} u(x,y)\\v(x,y)\\w(x,y) \end{array}\right)</math>. | ||
[[Datei:Schale-01.png|mini|Schalenmodell]] | |||
Aufgrund ihrer geringen Dicke können wir - wie bei [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] - Annahmen zu Spannungskomponenten treffen, die wir vernachlässigen dürfen. | [[Datei:Schale-01.png|mini|Schalenmodell]] Aufgrund ihrer geringen Dicke können wir - wie bei [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] - Annahmen zu Spannungskomponenten treffen, die wir vernachlässigen dürfen. | ||
In der Mechanik nutzen wir die geringe Dicke des Körpers, um vereinfachte Modelle für bestimmte Belastungsarten abzuleiten. | In der Mechanik nutzen wir die geringe Dicke des Körpers, um vereinfachte Modelle für bestimmte Belastungsarten abzuleiten. | ||
Aktuelle Version vom 21. April 2021, 13:03 Uhr
Unter einer Schale verstehen wir einen Körper, dessen Dicke sehr klein ist gegenüber seinen anderen Abmessungen. Alle Verschiebungen und Schnittlasten der Schale werden auf eine x-y-Referenzebene bezogen - wie beim Stab auf die Referenzachse x. Die Koordinaten der Schale sind demnach
- .
Aufgrund ihrer geringen Dicke können wir - wie bei Euler-Bernoulli-Balken - Annahmen zu Spannungskomponenten treffen, die wir vernachlässigen dürfen.
In der Mechanik nutzen wir die geringe Dicke des Körpers, um vereinfachte Modelle für bestimmte Belastungsarten abzuleiten.
So heißen Schalen,
- Scheibe, wenn sie bei einer ebenen Referenz-Konfiguration nur in ihrer x/y-Ebene belastet werden (ebener Spannungszustand)
- Platte, wenn sie bei einer ebenen Referenz-Konfiguration nur senkrecht zur x/y-Ebene belastet werden (Biegung) und
- Membran, wenn sie bei einer ebenen Referenz-Konfiguration und extrem geringer Dicke nur senkrecht zur x/y-Ebene belastet werden (keine Biegung, nur Spannungen in der verformten Ebene).
Gemeinsam ist diesen Modellen, dass sie die Verschiebung der materiellen Punkte P eines materiellen Punktes nur durch seine unabhängigen Koordinaten "x", "y" beschreiben können.