Sources/Lexikon/Modellbildung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 14: | Zeile 14: | ||
Physische Modelle zu bauen ist dabei meist sehr viel teurer, als Computer-Modell - oder mathematische Modelle - zu nutzen. Windkanal- Schlepptank- oder Flug-Versuche, Crash-Tests, Evakuierungen von Gebäuden etc. macht man nur, wenn es unbedingt sein muss. Viel billiger ist es meist, ein abstraktes "mathematisches" Modell zu entwickeln und im Computer zu implementieren. Diese abstrakten Modelle basieren auf Gleichungen, Bewegungsgleichungen von Systemen, die wir für verschiedene Realisierungen eines Systemes (Parameter) beliebig oft und preiswert wiederholen können. | Physische Modelle zu bauen ist dabei meist sehr viel teurer, als Computer-Modell - oder mathematische Modelle - zu nutzen. Windkanal- Schlepptank- oder Flug-Versuche, Crash-Tests, Evakuierungen von Gebäuden etc. macht man nur, wenn es unbedingt sein muss. Viel billiger ist es meist, ein abstraktes "mathematisches" Modell zu entwickeln und im Computer zu implementieren. Diese abstrakten Modelle basieren auf Gleichungen, Bewegungsgleichungen von Systemen, die wir für verschiedene Realisierungen eines Systemes (Parameter) beliebig oft und preiswert wiederholen können. | ||
Der Computer liefert uns die Möglichkeit, Modelle effizient zu nutzen und die Ergebnisse - z.B. grafisch - auszuwerten. | Der Computer liefert uns die Möglichkeit, Modelle effizient zu nutzen und die Ergebnisse - z.B. grafisch - auszuwerten. | ||
| Zeile 26: | Zeile 25: | ||
# Das mathematische Modell entsteht durch Anschreiben von Gleichungen - z.B. Gleichgewichtsbedingungen - für die einzelnen Teilkörper. | # Das mathematische Modell entsteht durch Anschreiben von Gleichungen - z.B. Gleichgewichtsbedingungen - für die einzelnen Teilkörper. | ||
# Das Modell wird dann im Rechner implementiert und gellöst - wir sagen: simuliert. Die Ergebnisse können wir dann ausdeuten. | # Das Modell wird dann im Rechner implementiert und gellöst - wir sagen: simuliert. Die Ergebnisse können wir dann ausdeuten. | ||
| Zeile 40: | Zeile 40: | ||
Diese acht Prozess-Schritte sind: | Diese acht Prozess-Schritte sind: | ||
Allgemeine Aufgabenstellung | === Allgemeine Aufgabenstellung === | ||
Aufgabe präzisieren | |||
System strukturieren | === Aufgabe präzisieren === | ||
Mathematisches Modell formulieren | |||
Mathematisches Modell anpassen | === System strukturieren === | ||
Computerprogramm schrieben | |||
Lösung berechnen und ausdeuten | === Mathematisches Modell formulieren === | ||
Rechenergebnisse mit beobachtetem Verhalten des Systems vergleichen | |||
=== Mathematisches Modell anpassen === | |||
=== Computerprogramm schrieben === | |||
=== Lösung berechnen und ausdeuten === | |||
=== Rechenergebnisse mit beobachtetem Verhalten des Systems vergleichen === | |||
Links | |||
* FEC1 | |||
Version vom 21. April 2021, 12:14 Uhr
Ein Modell ist ein Abbild der Wirklichkeit. Als Ingenieure suchen wir nach Modellen, die uns physikalische Systeme erklären. Um Modelle zu formulieren, brauchen wir das Fachwissen zu diesen Systemen, also die Mechanik, Chemie, Psychologie, Biologie usw. Ein Modell soll die Komplexität der Wirklichkeit reduzieren, um Zusammenhänge zu verstehen. Das Modell ist dabei nicht die Wirklichkeit. Das Modell erfasst bestimmte Aspekte der Wirklichkeit, die wir mindestens brauchen, um bestimmte Phänomene zu erklären. Wir wünschen uns Modelle, die so kompliziert wie nötig - aber so einfach wie möglich sind.

Modelle in der Wirtschaft
Um Modelle praktisch nutzen zu können, müssen wir sie meist in Mathematik "gießen" und in Computer-Programmen implementieren. Damit ist Google in wenigen Jahren zu einem der wertvollsten Unternehmen weltweit aufgestiegen. Das Produkt: ein Auktionsmodell für Werbung, das auf einem mathematischen Modell für die Wirksamkeit einer individuell plazierten Werbung auf einer Web-Seite basiert (aus [Zuboff 2018], vgl. [Google 2005]):
Der Algorithmus dazu:

Wir (hier in der Technischen Mechanik) nutzen Modelle, um physikalische Systeme (Autors, Fahrräder, etc.) zu entwickeln und zu konstruieren. Dabei gelingen uns Menschen nur die einfachsten Dinge auf der Basis von Intuition und erworbenen Erfahrungen. Komplexe Systeme erfordern auch hier immer eine Abstraktion, ein Modell, nach dem wir Prozesse oder Strukturen auslegen.
Dabei spielen physikalische und virtuelle Modelle eine Rolle, die oft Teil eines kreativen und innovativen Prozesses sind. So startete Henry Ford in seinem Werkraum mit einem Stück Rohr, um das Wirkprinzip des Verbrennungsmotors auszuprobieren. Und auch das Team Gates / Balmer starteten in ihrer Garage. Auch heute noch gebraucht man das Bild der Garage, um die Modellhaftigkeit einer Produkts, eines Prototyps zu erfassen. So gibt es zum Beispiel die Google-Garage, einer Werkstatt auf dem Firmengelände, die Werkstatt und Bastelraum für neue, innovative Ideen ist.
Physische Modelle zu bauen ist dabei meist sehr viel teurer, als Computer-Modell - oder mathematische Modelle - zu nutzen. Windkanal- Schlepptank- oder Flug-Versuche, Crash-Tests, Evakuierungen von Gebäuden etc. macht man nur, wenn es unbedingt sein muss. Viel billiger ist es meist, ein abstraktes "mathematisches" Modell zu entwickeln und im Computer zu implementieren. Diese abstrakten Modelle basieren auf Gleichungen, Bewegungsgleichungen von Systemen, die wir für verschiedene Realisierungen eines Systemes (Parameter) beliebig oft und preiswert wiederholen können.
Der Computer liefert uns die Möglichkeit, Modelle effizient zu nutzen und die Ergebnisse - z.B. grafisch - auszuwerten.
Computer-Modelle
Sie sind heute das zentrale Werkzeug, um kosteneffizient Systeme zu modellieren und zu simulieren. "FEM", "CFD", "MBS" sind heute die Überschriften zu Simulationspaketen, die Modelle semi-automatisiert im Rechner erzeugen, die Modelle lösen (simulieren) und Ergebnisse anschaulich darstellen.
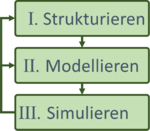
Der Gesamt-Prozess dazu verläuft in drei Teilen.
- Zum Strukturieren einer Aufgabe gehören die Auftragsklärung. Man einigt sich mit dem Auftraggeber darauf, wie das Modell gegenüber der Umgebung abgegrenzt ist und welche Wechselwirkungen es mit der Umgebung hat. Das System wird in Teilsysteme oder Teilkörper unterteilt und man überlegt sich Koordinaten bzw. Zustandsgrößen, mit denen man das Modell beschreiben will.
- Das mathematische Modell entsteht durch Anschreiben von Gleichungen - z.B. Gleichgewichtsbedingungen - für die einzelnen Teilkörper.
- Das Modell wird dann im Rechner implementiert und gellöst - wir sagen: simuliert. Die Ergebnisse können wir dann ausdeuten.
Fast immer ist das ein iterativer Prozess, den man so lange durchläut, bis man zufriedenstellende Ergebnisse hat.
Die drei Teile gliedern wir wiederum in Prozess-Schritte:
| I Strukturieren | 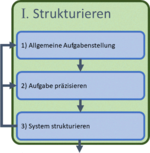 |
|---|---|
| II Modellieren | 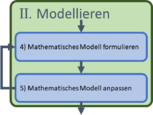 |
| III Simulieren | 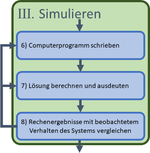 |
Diese acht Prozess-Schritte sind:
Allgemeine Aufgabenstellung
Aufgabe präzisieren
System strukturieren
Mathematisches Modell formulieren
Mathematisches Modell anpassen
Computerprogramm schrieben
Lösung berechnen und ausdeuten
Rechenergebnisse mit beobachtetem Verhalten des Systems vergleichen
Links
- FEC1