Sources/Lexikon/Lösungsschema der Statik: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
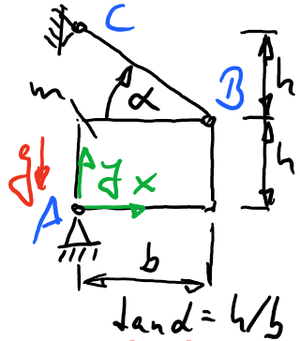
Lageplan 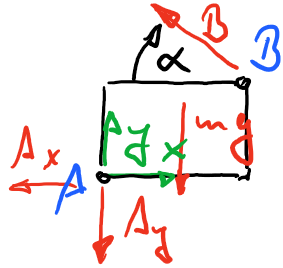
Freikörperbild 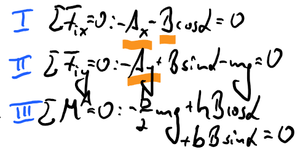
Gleichgewichtsbedingungen 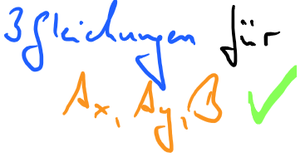
Gleichungen und Unbekannte abzählen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 19: | Zeile 19: | ||
==Lösen== | ==Lösen== | ||
[[Datei:Schema-5-2-.png|rahmenlos]] | [[Datei:Schema-5-2-.png|rahmenlos]] | ||
... liefert | |||
::<math>\begin{pmatrix}{{A}_{x}}=\displaystyle -\frac{\cos\left( \alpha\right) \cdot b\cdot g\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\cr {{A}_{y}}=\displaystyle -\frac{\sin\left( \alpha\right) \cdot b\cdot g\cdot m+2\cdot \cos\left( \alpha\right) \cdot g\cdot h\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\cr B=\displaystyle \frac{b\cdot g\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\end{pmatrix}</math>. | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Maxima Code | |||
|text=Ein Skript zur Lösung in Maxima: | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* Maxima */ | |||
equs: [-A[x]-B*cos(alpha) = 0, | |||
-A[y]+B*sin(alpha) -m*g = 0, | |||
-b/2*m*g+h*B*cos(alpha) + b*B*sin(alpha) = 0]; | |||
q : [A[x],A[y],B]; | |||
sol: solve(equs,q)[1]; | |||
</syntaxhighlight> | |||
}} | |||
==Ausdeuten der Lösung== | ==Ausdeuten der Lösung== | ||
[[Datei:Schema-6-2-.png|rahmenlos]] | [[Datei:Schema-6-2-.png|rahmenlos]] | ||
Achtung, das System in statisch unbestimmt, wenn die Systemdeterminante D verschwindet, also | |||
::<math>\mathrm{cos}\left( \alpha\right) \cdot h+\mathrm{sin}\left( \alpha\right) \cdot b = 0</math> | |||
Das passiert für | |||
::<math>\tan \alpha = h/b</math> | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Maxima Code | |||
|text=Ein Skript zur Ausdeutung der Lösung in Maxima: | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
D: determinant(submatrix(augcoefmatrix(equs,q),4)); | |||
</syntaxhighlight> | |||
}} | |||
Version vom 21. April 2021, 09:55 Uhr
Lageplan

Freikörperbild

Gleichgewichtsbeidngungen
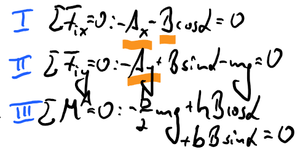
Gleichungen und Unbekannte abzählen
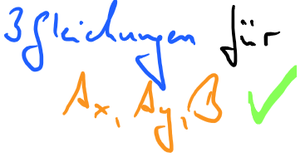
Lösen
- Fehler beim Parsen (Unbekannte Funktion „\cr“): {\displaystyle \begin{pmatrix}{{A}_{x}}=\displaystyle -\frac{\cos\left( \alpha\right) \cdot b\cdot g\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\cr {{A}_{y}}=\displaystyle -\frac{\sin\left( \alpha\right) \cdot b\cdot g\cdot m+2\cdot \cos\left( \alpha\right) \cdot g\cdot h\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\cr B=\displaystyle \frac{b\cdot g\cdot m}{2\cdot \cos\left( \alpha\right) \cdot h+2\cdot \sin\left( \alpha\right) \cdot b}\end{pmatrix}} .
Maxima Code
Ein Skript zur Lösung in Maxima:
/* Maxima */
equs: [-A[x]-B*cos(alpha) = 0,
-A[y]+B*sin(alpha) -m*g = 0,
-b/2*m*g+h*B*cos(alpha) + b*B*sin(alpha) = 0];
q : [A[x],A[y],B];
sol: solve(equs,q)[1];
Ausdeuten der Lösung
![]() Achtung, das System in statisch unbestimmt, wenn die Systemdeterminante D verschwindet, also
Achtung, das System in statisch unbestimmt, wenn die Systemdeterminante D verschwindet, also
Das passiert für
Maxima Code
Ein Skript zur Ausdeutung der Lösung in Maxima:
D: determinant(submatrix(augcoefmatrix(equs,q),4));
