Sources/Lexikon/Reibkennlinie

Koordinanten und Schnittkräfte

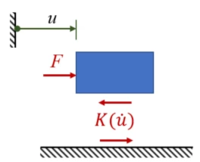
Reiben oder haften Körper aneinander, so wird ihre geschwindigkeitsabhängige Kontaktkraft K(v) in der Tangentialebene oft durch den Reib- und Haftbeiwert μ bzw. μ₀ beschreiben:

$\begin{array}{ccrl}|K|& <& {\mu }_0\cdot N& \text{ für }v=0\\ K& =& \mu \cdot N& \text{ für }v>0\\ K& =& -\mu \cdot N& \text{ für }v<0\end{array}$

mit

$v=\dot{u}$

Erster Ansatz mit Geradenstücken

Kennlinie (erster Anlauf)

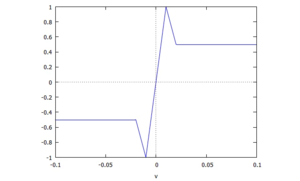
Statt zwischen Haften und Reiben zu unterscheiden, kann man mit folgender Kennlinie arbeiten, die Schaltstellen für v₀ = +/- ε hat.

Die stückweise definierte Funktion ist:

$K=N\cdot \{\begin{array}{ll}-\mu & \text{ für }v<=-2ϵ\\ +\mu & \text{ für }v>=+2ϵ\\ -((2{\mu }_0-\mu )ϵ+({\mu }_0-\mu )v)/ϵ& \text{ für }v<=-ϵ\\ -((\mu -2{\mu }_0)ϵ+({\mu }_0-\mu )v)/ϵ& \text{ für }v>=+ϵ\\ {\mu }_0(v/ϵ);& \text{ sonst}\end{array}$

Maxima Code

Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.

📑 toggle code

/* friction characteristic */
/* piecewise linear        */

subst(solve([c[0]+c[1]*(+epsilon)=+b,c[0]+c[1]*2*(+epsilon)=+a],[c[0],c[1]])[1],c[0]+c[1]*v)
mu(a,b,epsilon,v) := if     v<=-2*epsilon then -a
                     elseif v>=+2*epsilon then +a
                     elseif v<=  -epsilon then -((2*b-a)*epsilon+(b-a)*v)/epsilon
                     elseif v>=  +epsilon then -((a-2*b)*epsilon+(b-a)*v)/epsilon
                     else                      b*(v/epsilon);  
                     
plot2d(mu(0.5,1,0.01,v),[v,-0.1,0.1], [ylabel,"v/V->"], [xlabel,"μ/1->"], [legend, "friction coefficient"]);

Video abspielen

Lokale Datei

Lokale Datei sammelt möglicherweise persönliche Daten.

FortfahrenAusblenden

Erläuterungen zur Reibkennlinie

Und so funktionierts:Steigert man die Kraft F  auf den Körper, so "kriecht" der Körper - seine Geschwindigkeit v bleibt sehr klein. Wählt man also die Schaltstellen v₀ = +/- ε passend klein, dann sieht es so aus, als würde der Körper "haften". Überschreitet F die maximale Haftkraft, also F > μ₀∙N, dann fällt μ(v) auf den Reib-Beiwert ab, der Körper wird beschleunigt.

Das Problem: diese Kennlinie ist nicht stetig differenzierbar - Löser, die das zur Schrittweiten-Steuerung voraussetzen "fressen" sich an den Schaltstellen fest.

Verbesserter Ansatz: stückweise mit einem Polynom 5ten Grades

Stetig differenzierbare Reibkennlinie mit einem Polynom 5ter Ordnung (aus Kv53)

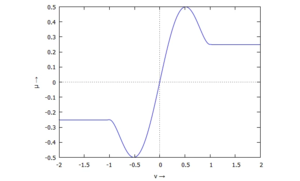
Um eine stetig differenzierbare Reibkennlinie zu erhalten, setzten wir stückweise ein Polynom an. Es soll Punkt-symmetrisch sowie an den Übergangsstellen stetig und stetig differenzierbar sein!

Hier arbeiten wir mit der dimensionslosen Geschwindigkeit

$\nu =\frac{v}{v_0}$

und setzen für den mittleren Teil -v₀ < v < v₀ das Polynom

$\mu =a_1\cdot {\nu }^1+a_3\cdot {\nu }^3+a_5\cdot {\nu }^5$.

an.

Dann ist - hier für μ₀=1/2 und μ=1/4:

$K=N\cdot \{\begin{array}{ll}-\mu & \text{ für }\nu <=-1\\ +\mu & \text{ für }\nu >=+1\\ 1.2{\nu }^5-2.5{\nu }^3+1.5\nu & \text{ sonst}\end{array}$

Maxima Code

Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.

📑 toggle code

/* parameter */
params: [mu[0]   = 1/2,
         mu[1]   = 1/4]$ 

/**** define nonlinear friction characteristic ***/
/*    choose generic polynom */
p : lsum(a[i]*nu^i,i,[1,3,5]);
mu(nu,charc) := if abs(nu)<1 then subst(charc, lsum(a[i]*nu^i,i,[1,3,5])) else subst(charc, mu[1])*signum(nu);
/*    ... and adapt to these conditions  */
bcs : [subst([nu=  1  ],      p    ) = mu[1],
       subst([nu=  1  ], diff(p,nu)) = 0    ,
       subst([nu=gamma], diff(p,nu)) = 0    ,
       subst([nu=gamma],      p    ) = mu[0]];
coe : [a[1],a[3],a[5],gamma];
sol: solve(subst(params,bcs),coe)$

charc : append(params,sol[1]);
plot2d(mu(nu,charc),[nu,-2,2], [xlabel,"ν →"], [xlabel,"μ →"])$

Die Gleichung für die Kennlinie können wir nicht analytisch explizit angeben - Sie können die Kennlinie also nicht ohne Maxima in ein anderes Programm übertragen.

Abhilfe schafft dieser Ansatz:

Verbesserter Ansatz: stückweise mit Polynomen 2ten und 3ten Grades

Skizze: Stetig differenzierbare Reibkennlinie mit angestückelten Polynomen.

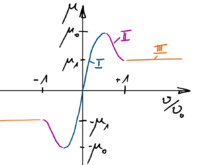
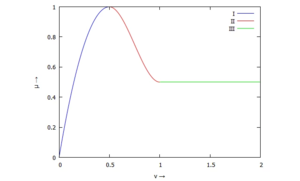
Wir bleiben bei der stetig differenzierbaren Reibkennlinie, suchen nun aber nach einfacheren Polynomen, deren Koeffizienten wir auch explizit in μ₀ und μ angeben können. Alles hat seinen Preis: wir brauchen nun zwei Polynome (I und II)für den ersten Teil!

Wir arbeiten weiter mit

$\nu =\frac{v}{v_0}$

und setzen für den mittleren Teil -v₀ < v < v₀ nun zwei Polynome

$\begin{array}{llllll}{\mu }_I& =& & a_{I,2}\cdot {\nu }^2& +a_{I,1}\cdot \nu & \\ {\mu }_{II}& =& a_{II,3}\cdot {\nu }^3+& a_{II,2}\cdot {\nu }^2& +a_{II,1}\cdot \nu & +a_{II,0}\end{array}$

an.

Dann ist

$K=N\cdot \{\begin{array}{ll}+\mu & \text{ für }+1<\nu \\ 16\cdot {\mu }_0(1-\frac{{\mu }_1}{{\mu }_0})\cdot {\nu }^3-36\cdot {\mu }_0(1-\frac{{\mu }_1}{{\mu }_0})\cdot {\nu }^2+24\cdot {\mu }_0(1-\frac{{\mu }_1}{{\mu }_0})\cdot \nu +5\cdot {\mu }_1-4\cdot {\mu }_0& \text{ für }+\frac{1}{2}<\nu <=+1\\ 4\cdot {\mu }_0\cdot (\nu -{\nu }^2)& \text{ für }0<\nu <=+\frac{1}{2}\\ \text{und punktsymmetrisch}& \text{ sonst}\end{array}$

Ein Ausschnitt der Kennlinie mit den Abschnitten I, II und III

Maxima Code

Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.

📑 toggle code

/* parameter */
params : [mu[0]=1, mu[1] = 0.5];

/**** define nonlinear friction characteristic ***/
/*    choose generic polynoms for three sections */
r : [sum(a[i]*nu^i,i,0,2),
     sum(a[i]*nu^i,i,0,3),
     mu[1]];

/*    ... and adapt to these conditions  */
sol: [solve([subst([nu=   0     ],     r[1])          =  0,
             subst([nu=1/2],     r[1])          = mu[0],
             subst([nu=1/2],diff(r[1],nu)) = 0], [a[2],a[1],a[0]])[1],
      solve([subst([nu=1/2],     r[2])          = mu[0],
             subst([nu=1  ],     r[2])          = mu[1],
             subst([nu=1/2],diff(r[2],nu)) = 0,
             subst([nu=1  ],diff(r[2],nu)) = 0], [a[3],a[2],a[1],a[0]])[1]];

r : ratsimp([subst(sol[1],r[1]),subst(sol[2],r[2]),r[3]]);
print(transpose(r));

/*    ... and plot ...                 */
r : subst(nu=t,subst(params,r));
plot2d([[parametric, t, r[1], [t,  0 ,1/2]],
        [parametric, t, r[2], [t, 1/2, 1 ]],
        [parametric, t, r[3], [t,  1 , 2 ]]], [legend,"I","II","III"],
        [xlabel,"ν →"], [ylabel,"μ →"])$

Hier ist die tangentiale Kontaktkraft konstant, wenn der Körper eine relevante Relativgeschwindigkeit gegenüber seiner Unterlage hat. Diese Vorstellung passt oft nicht mit Messungenüberein - außerdem gibt es einen weiteren Nachteil: Die Kennlinie fällt nur in einem ganz kleinen Bereich und es wird schwer, damit im Modell eine Selbsterregung zu erzeugen.

Besser geht das mit einer stetig fallenden Kennlinie:

Stetig fallende Reibkennlinie

Die gesuchte stetig differenzierbare Kennlinie μ(ν) mit stetig abnehmendem Reibkoeffizienten setzen wir aus sin- und e-Funktion zusammen.

Sie muss punkt-symmetrisch sein (die Reibkraft ändert ihr Vorzeichen mit der Orientierung der Relativgeschwindigkeit). Die Sinus-Funktion verwenden wir für den Mittelteil (Haften) und die Exponential-Funktionen für die Gebiete, in denen die Körper aufeinander reiben.:

Reibkennline mit stetig fallender Charakteristik - aus Aufgabe Kw25

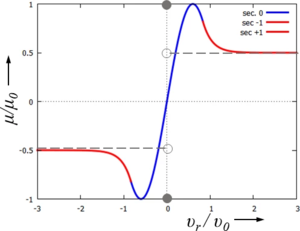
Im Mittelteil (blau) setzen wir für die Sinus-Funktion an

mit

.

Dieses Mittelteil stückeln wir stetig differenzierbar jeweils an eine Exponentialfunktion mit den Parametern E und κ an, hier

mit

.

Damit ist

die gesuchte Kennlinie.

---

Maxima Code

Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.

📑 toggle code

/*  define degressive friction characteristics */
/*********************************************************/
/* parameter */
params: [a=1/2, b = 5/6, V0=0.001];

ch : [sin(b*%pi*nu),0,0];
 
ch[2]: E*%e^(kappa*(nu+b))-a;
ch[2] : subst(solve([subst([nu=-b],ch[2]=ch[1]),subst([nu=-b],diff(ch[2]=ch[1],nu))],[E,\kappa])[1],ch[2]);
ch[3] : subst([nu=-nu],-ch[2]);
plot2d([[parametric, t, subst(params,subst(t,nu,ch[1])),subst(params,[t,-b, b])],
        [parametric, t, subst(params,subst(t,nu,ch[2])),subst(params,[t,-3,-b])],
        [parametric, t, subst(params,subst(t,nu,ch[3])),subst(params,[t,+b,+3])]],[legend,"sec. 0","sec -1","sec +1"],
        [y,-1,1],
        [style, [lines,3,1], [lines,3,2], [lines,3,2]], [xlabel, "Geschwindigkeit v/V0 →"], [ylabel, "Reib-Koeffizient μ/1 →"])$
 
/**** define nonlinear friction characteristic ***/
fric(nu, a,b) :=
  if nu < -b then
     (a-sin(%pi*b^2))*%e^(-(%pi*b*cos(%pi*b^2)*(b+nu))/(sin(%pi*b^2)-a))-a       /*ch[2]*/
  elseif nu > +b then
     a-(a-sin(%pi*b^2))*%e^(-(%pi*b*cos(%pi*b^2)*(b-nu))/(sin(%pi*b^2)-a))       /*ch[3]*/
  else
     sin(%pi*b*nu)                                                               /*ch[1]*/
     ;

Links

• Kw25