Sources/Lexikon/Eulersche Winkel: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 30: | Zeile 30: | ||
Die Lage der Koordinatenachsen für diese beiden Koordinatensysteme sehen sie hier: | Die Lage der Koordinatenachsen für diese beiden Koordinatensysteme sehen sie hier: | ||
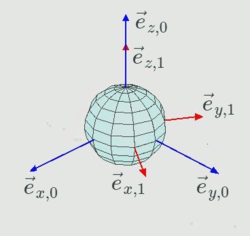
[[Datei:Euler2a-step-1+.png|links|mini|Koordinaten zur Euler-Transformation]] | [[Datei:Euler2a-step-1+.png|links|mini|250px|Koordinaten zur Euler-Transformation]] | ||
Die Transformations-Matrix | |||
::<math>\underline{\underline{D}}_3(\varphi)</math> | |||
heißt Drehmatrix. Sie dreht das (blaue) Koordinatensystem um den Winkel φ bezüglich der z- (3-) Achse und ist | |||
::<math>\displaystyle \underline{\underline{D}}_3(\varphi) =\left(\begin{array}{ccc}\;\;\;\cos \varphi & \sin \varphi & 0\\-\sin \varphi & \cos \varphi & 0\\0&0&1\end{array}\right)</math>. | |||
Eine Abfolge von von Drehungen um die um die z0-, y1- und x2-Achse wie in der Animation oben erfassen wir dann also durch | |||
::<math>\underline{\vec{e}}_1=\underline{\underline{D}}_1(\varphi_1)\cdot \underline{\underline{D}}_2(\varphi_2)\cdot \underline{\underline{D}}_3(\varphi_3)\cdot \underline{\vec{e}}_0</math>. | |||
Auch hier wird ersichtlich; die Abfolge der Drehungen ist nicht beliebig, weil die Matrizen-Multiplikation nicht kommutativ ist! | |||
Version vom 21. April 2021, 06:22 Uhr
Wenn wir in technischen Systemen die Bewegung eines Körpers (Flugzeug, Roboterarm, ...) beschreiben, brauchen wir dafür Koordinaten der Translation (hier u und v) und der Rotation (hier φ).
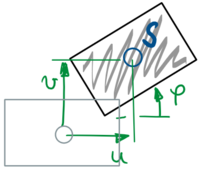
Bei zweidimensionalen Problemen ist das - wie oben - anschaulich und bereitet keine mathematischen Schwierigkeiten.
This is a file from the Wikimedia Commons. |
Bei Drehungen im Raum wird es komplizierter: wir müssen formaler vorgehen.
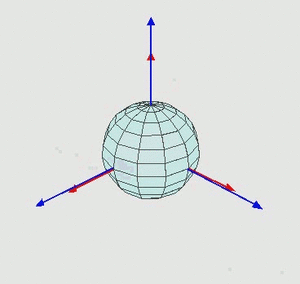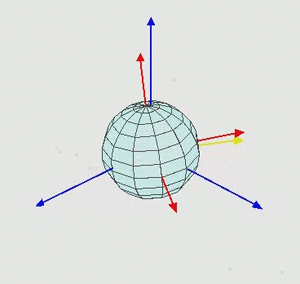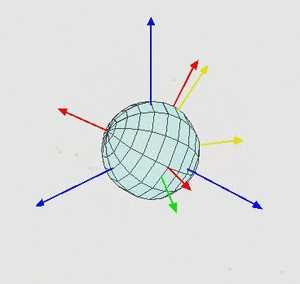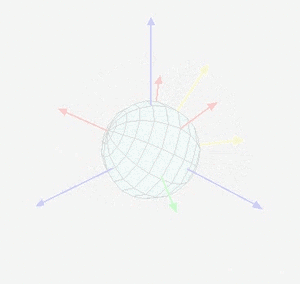
Dazu beschrieben wir - wie in der Animation links - eine Drehung des Körpers durch eine sukzessive Drehung aus seinem Koordinatensystem in der Referenzlage (blau) in sein körperfestes Koordinatensystem (rot).
Die drei Drehungen heißen Euler-Winkel und die Abfolge der Drehungen ist relevant: der Köper wird durch eine Abfolge von Drehungen um seine jeweiligen Körperachsen beschrieben!
In der Luftfahrt heißen die Drehungen Roll-, Nick- und Gierwinkel und gehören zu Drehungen um die z0-, y1- und x2-Achse.
Bei jeder Drehung werden die Einheits-Richtungsvektoren
um einen Winkel bezüglich einer Achse gedreht. So wird die erste Drehung des Referenz-Koordinatensystems mit Index "0" um die vertikale (z-) Achse gedreht - die Transformationsbeziehung lautet
- .
Die Lage der Koordinatenachsen für diese beiden Koordinatensysteme sehen sie hier:
Die Transformations-Matrix
heißt Drehmatrix. Sie dreht das (blaue) Koordinatensystem um den Winkel φ bezüglich der z- (3-) Achse und ist
- .
Eine Abfolge von von Drehungen um die um die z0-, y1- und x2-Achse wie in der Animation oben erfassen wir dann also durch
- .
Auch hier wird ersichtlich; die Abfolge der Drehungen ist nicht beliebig, weil die Matrizen-Multiplikation nicht kommutativ ist!