Sources/Lexikon/Euler-Bernoulli-Balken: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
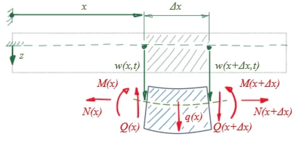
Koordinaten und Schnittgrößen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Ein Modell für schlanke Stäbe, bei der die elastische Verformung durch innere Momente erfasst wird. | [[Datei:Euler-Bernoulli-Balken.png|mini|Koordinaten und Schnittgrößen]]Ein Modell für schlanke Stäbe, bei der die elastische Verformung nur durch innere Momente erfasst wird heißt Euler-Bernoulli-Blaken. | ||
Annahmen für das Modell: | Annahmen für das Modell: | ||
| Zeile 5: | Zeile 5: | ||
* Querschnitte bleiben eben; | * Querschnitte bleiben eben; | ||
* Querschnitte bleiben senkrecht zur [[Sources/Lexikon/Euler-Bernoulli-Balken/Neutrale Faser|Neutralen Faser]]; | * Querschnitte bleiben senkrecht zur [[Sources/Lexikon/Euler-Bernoulli-Balken/Neutrale Faser|Neutralen Faser]]; | ||
Eine Theorie, die auch die Schubverformung der Querschnitte berücksichtigt ist der [[Sources/Lexikon/Timoshenko-Balken|Timoshenko-Balken]]. | |||
<table class="wikitable" style="background-color:white; margin-right:14px; | Einen Einblick in die Theorie gibt [[Gelöste Aufgaben/DGEB|DGEB]].<table class="wikitable" style="background-color:white; margin-right:14px; | ||
"> | "> | ||
<tr><th>Biegedifferentialgleichung 4.ter Ordnung</th><th>Formänderungs-Energie</th></tr> | <tr><th>Biegedifferentialgleichung 4.ter Ordnung</th><th>Formänderungs-Energie</th></tr> | ||
<tr><td></td><td></td></tr> | <tr><td> | ||
* <math>\displaystyle \frac{d^2}{dx^2}M(x) = -q(x) \text{ und mit } M(x) = -E\,I\,w''(x)</math> | |||
* <math>\displaystyle \frac{d^2}{dx^2} \left( E\,I \cdot \frac{d^2}{dx^2} w(x)\right) = +q(x)</math> | |||
Oft können wir davon ausgehen, dass ''E'' und ''I'' konstant sind, dann gilt | |||
* <math>\displaystyle E\,I\, w^{IV} = q \;\;\text{ mit }\;\; w^{IV} := \frac{d^4}{dx^4}(w)</math> | |||
</td><td>Für das Verfahren von Ritz und die Methode der Finiten Elemente brauchen wir die [[Sources/Lexikon/Formänderungsenergie|Formänderungsenergie]] | |||
<math>\Pi_{EBB} = \displaystyle \frac{1}{2}\int_0^\ell E\,I \cdot w''^2 dx</math> | |||
bzw. | |||
<math>\delta \Pi_{EBB} = \displaystyle \int_0^\ell E\,I \cdot w''\cdot \delta w'' dx</math> | |||
Und beide Formulierungen gelten unabhängig davon, ob ''E'' und ''I'' konstant sind - oder nicht. | |||
</td></tr> | |||
</table> | </table> | ||
Seiten dazu:<splist showparent="no" | |||
Seiten dazu:<splist showparent="no" sort="asc" sortby="title" liststyle="unordered" showpath="no" kidsonly="yes" debug="0" /> | |||
Version vom 21. April 2021, 05:40 Uhr

Ein Modell für schlanke Stäbe, bei der die elastische Verformung nur durch innere Momente erfasst wird heißt Euler-Bernoulli-Blaken.
Annahmen für das Modell:
- Querschnitte bleiben eben;
- Querschnitte bleiben senkrecht zur Neutralen Faser;
Eine Theorie, die auch die Schubverformung der Querschnitte berücksichtigt ist der Timoshenko-Balken.
Einen Einblick in die Theorie gibt DGEB.
| Biegedifferentialgleichung 4.ter Ordnung | Formänderungs-Energie |
|---|---|
|
Oft können wir davon ausgehen, dass E und I konstant sind, dann gilt | Für das Verfahren von Ritz und die Methode der Finiten Elemente brauchen wir die Formänderungsenergie
bzw.
Und beide Formulierungen gelten unabhängig davon, ob E und I konstant sind - oder nicht. |
Seiten dazu: