Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken

Diese Seite fasst die wichtigsten Ergebnisse für die FEM-Formulierung zum Euler-Bernoulli-Balken zusammen.

Maxima-Code für die Element-Matrizen

Hier finden Sie den Sourcecode für die Herleitung der Element-Matrizen.

/*Maxima Quellcode für die Erzeugung Inhalte dieser Seite */
/* Maxima version 16.04.2*/

declare( "ℓ", alphabetic);

/*Trial-Fucntions*/
phi : [       (xi-1)^2*(2*xi+1),
         ℓ[i]* xi     *(  xi-1)^2,
        -      xi^2   *(2*xi-3), 
         ℓ[i]* xi^2   *(  xi-1)];

/* depict independant and dependant coordinates */
preamble: "set yrange [] reverse";
plot2d(subst([ℓ[i]=1],[0.9,1/2,0.1,1/3].phi),[xi,0,1],
    [x,0,1], [legend, "w(x)"],
    [xlabel, "ξ →"], [ylabel, "← w"],
    [gnuplot_preamble, preamble]);

/* plot trial-functions parameters */
scale: [1,1/ℓ[i],1,1/ℓ[i]];
colours: [blue, red, green, magenta];
legends: ["ϕ1","ϕ2/ℓ[i]","ϕ3","ϕ4/ℓ[i]"];
for j:1 thru 4 do
     (plot2d(scale[j]*phi[j],[xi,0,1], [xlabel,"ξ →"],[ylabel,"ϕ →"], [legend,legends[j]],[color,colours[j]], [style, [lines,3]], same_xy,
              [gnuplot_preamble, "set xtics 1;set ytics 1;set tics font \",11\""]))$	

/* Element-Mass Matrix */
M[i] : funmake('matrix,makelist(makelist(rho*A*integrate(phi[j]*phi[k],xi,0,1)*ℓ[i],j,1,4),k,1,4));
/*       (rho*A*ℓ[i])*matrix([13/35,(11*ℓ[i])/210,9/70,-(13*ℓ[i])/420],
                             [(11*ℓ[i])/210,ℓ[i]^2/105,(13*ℓ[i])/420,-ℓ[i]^2/140],
                             [9/70,(13*ℓ[i])/420,13/35,-(11*ℓ[i])/210],
                             [-(13*ℓ[i])/420,-ℓ[i]^2/140,-(11*ℓ[i])/210,ℓ[i]^2/105])  */
/* Element-Striffness Matrix */
K[i] : funmake('matrix,makelist(makelist(EI*integrate(diff(phi[j],xi,2)/ℓ[i]^2*diff(phi[k],xi,2)/ℓ[i]^2,xi,0,1)*ℓ[i],j,1,4),k,1,4));
/*       (EI/ℓ[i]^3)*matrix([12,6*ℓ[i],-12,6*ℓ[i]],
                            [6*ℓ[i],4*ℓ[i]^2,-6*ℓ[i],2*ℓ[i]^2],
                            [-12,-6*ℓ[i],12,-6*ℓ[i]],
                            [6*ℓ[i],2*ℓ[i]^2,-6*ℓ[i],4*ℓ[i]^2])   */

Trial-Functions

Die Koordinaten eines Finiten Elements sind

${\underline {Q}}(t)=\left({\begin{array}{l}W_{i-1}(t)\\\Phi _{i-1}(t)\\W_{i}(t)\\\Phi _{i}(t)\end{array}}\right)$.

Der Ansatz für die Näherung der Auslenkung w(x,t) ist

$\displaystyle w(x,t)=\sum _{i=1}^{4}Q_{i}(t)\cdot \phi _{i}(x)$

Die Drehwinkel sind hier so gewählt, dass 

$\displaystyle {\frac {d}{dx}}w(x)|_{x=x_{i}}=\Phi _{i}$.

Nodal and independent Coordinates

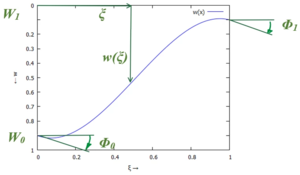
Trialfunctions

Die einzelnen Trial-Functions sind:

linker Rand (Knoten "i-1")	rechter Rand (Knoten "i")
Trial-Function for Wi-1	Trial-Function for Wi
$\phi _{1}(\xi )=(\xi -1)^{2}\cdot (2\;\xi +1)$	$\phi _{3}(\xi )=\xi ^{2}\cdot (3-2\;\xi )$
Trial-Function für Φi-1	Trial-Function für Φi
$\phi _{2}(\xi )=\ell _{i}\cdot \xi \cdot (\xi -1)^{2}$	$\phi _{4}(\xi )=\ell _{i}\cdot \xi ^{2}\cdot (\xi -1)$

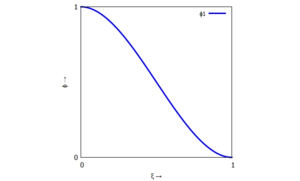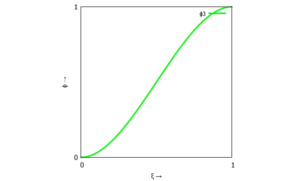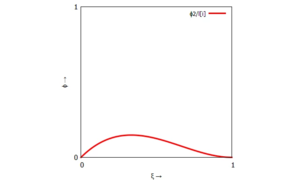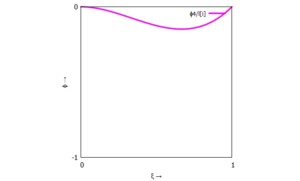Faltungsintegrale

... für die symmetrische Massenmatrix

Tabelliert sind die Werte der Integrale

$\displaystyle {\frac {m_{ij}}{\varrho A}}=\int _{0}^{\ell }\phi _{i}\cdot \phi _{j}\;dx$

	$\phi _{1}$	$\phi _{2}$	$\phi _{3}$	$\phi _{4}$
$\phi _{1}$	$\displaystyle {\frac {13}{35}}\;\ell _{i}$	$\displaystyle {\frac {11}{210}}\;\ell _{i}^{2}$	$\displaystyle {\frac {9}{70}}\;\ell _{i}$	$\displaystyle -{\frac {13}{420}}\;\ell _{i}^{2}$
$\phi _{2}$		$\displaystyle {\frac {1}{105}}\;\ell _{i}^{3}$	$\displaystyle {\frac {13}{420}}\;\ell _{i}^{2}$	$\displaystyle -{\frac {1}{140}}\;\ell _{i}^{4}$
$\phi _{3}$			$\displaystyle {\frac {13}{35}}\;\ell _{i}$	$\displaystyle {\frac {11}{210}}\;\ell _{i}^{2}$
$\phi _{4}$	symm.			$\displaystyle {\frac {1}{105}}\;\ell _{i}^{3}$

... für die symmetrische Steifigkeitsmatrix

Tabelliert sind die Werte der Integrale

$\displaystyle {\frac {k_{ij}}{EI}}=\int _{0}^{\ell }\phi _{i}''\cdot \phi _{j}''\;dx$

	$\phi ''_{1}$	$\phi ''_{2}$	$\phi ''_{3}$	$\phi ''_{4}$
$\phi ''_{1}$	$\displaystyle {\frac {12}{\ell _{i}^{3}}}$	$\displaystyle {\frac {6}{\ell _{i}^{2}}}$	$\displaystyle -{\frac {12}{\ell _{i}^{3}}}$	$\displaystyle {\frac {6}{\ell _{i}^{2}}}$
$\phi ''_{2}$		$\displaystyle {\frac {4}{\ell _{i}}}$	$\displaystyle -{\frac {6}{\ell _{i}^{2}}}$	$\displaystyle {\frac {2}{\ell _{i}}}$
$\phi ''_{3}$			$\displaystyle {\frac {12}{\ell _{i}^{3}}}$	$\displaystyle -{\frac {6}{\ell _{i}^{2}}}$
$\phi ''_{4}$	symm.			$\displaystyle {\frac {4}{\ell _{i}}}$

Maxima-Code für die Rechte-Seite

Hier finden Sie den Sourcecode für die Herleitung der Spalten-Matrizen der Rechten-Seite des Gleichungssystems.

/*Loadiung-Fucntions*/
psi: [1,
      (1-xi),
      xi,
      4*(-xi^2+xi)];

for j:1 thru length(psi) do
   plot2d(psi[j],[xi,0,1], [y,-0.1,1.1],
      [box, false], grid2d,
      [yx_ratio, 1], [axes, solid], [xtics, 0, 1, 1],
      [ytics, 0, 1, 1],
      [ylabel, simplode (["ϕ[",j,"] →"])],
      [xlabel, "ξ →"],
      [style,[lines,3,2]])$

/* convolution integrals */
for i:1 thru length(phi) do
   (print("***************************", i),
    for j:1 thru length(psi) do 
       print(integrate(phi[i]*psi[j],xi,0,1)))$

... für die rechte Seite des Gleichungssystems - aus äußeren, einprägten Lasten wie z.B. Streckenlasten q₀∙ψ

Die virutelle Arbeit dieser äußeren Streckenlast ist

$\displaystyle \delta W^{a}=q_{0}\int _{0}^{\ell }\psi (x)\cdot \delta w(x)\;\,dx$

                       Hier stehen die Faltungsintegrale beispielhaft für 

${\begin{array}{l}\psi _{1}=1\\\psi _{2}=1-\xi \\\psi _{3}=\xi \\\psi _{4}=4\cdot \left(\xi -{{\xi }^{2}}\right)\end{array}}$

Werte von $\displaystyle \int _{0}^{1}\phi _{i}\cdot \psi _{j}\;d\xi$	$\phi _{1}$	$\phi _{2}$	$\phi _{3}$	$\phi _{4}$
$\psi _{1}$	$\displaystyle {\frac {1}{2}}$	$\displaystyle {\frac {\ell _{i}}{12}}$	$\displaystyle {\frac {1}{2}}$	$\displaystyle -{\frac {\ell _{i}}{12}}$
$\psi _{2}$	$\displaystyle {\frac {7}{20}}$	$\displaystyle {\frac {\ell _{i}}{20}}$	$\displaystyle {\frac {3}{20}}$	$\displaystyle -{\frac {\ell _{i}}{30}}$
$\psi _{3}$	$\displaystyle {\frac {3}{20}}$	$\displaystyle {\frac {\ell _{i}}{30}}$	$\displaystyle {\frac {7}{20}}$	$\displaystyle -{\frac {\ell _{i}}{20}}$
$\psi _{4}$	$\displaystyle {\frac {1}{3}}$	$\displaystyle {\frac {\ell _{i}}{15}}$	$\displaystyle {\frac {1}{3}}$	$\displaystyle -{\frac {\ell _{i}}{15}}$

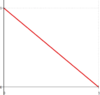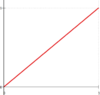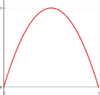Virtuelle Arbeiten

... der D'Alembert'sche Trägheitskräfte eines Finiten Elements

$\delta W^{a}=\displaystyle \int _{\displaystyle \ell _{i}}\varrho \;A\;{\ddot {w}}_{i}\cdot \delta w_{i}\;dx_{i}$

ist

$\delta W_{i}^{a}=-\left({{\mathit {\delta W}}_{i-1}},{{\mathit {\delta \Phi }}_{i-1}},{{\mathit {\delta W}}_{i}},{{\mathit {\delta \Phi }}_{i}}\right)\cdot \displaystyle {\mathit {\varrho A\ell _{i}}}\cdot {\begin{pmatrix}\displaystyle {\frac {13}{35}}&\displaystyle {\frac {11{\ell _{i}}}{210}}&\displaystyle {\frac {9}{70}}&\displaystyle -{\frac {13{\ell _{i}}}{420}}\\\displaystyle {\frac {11{\ell _{i}}}{210}}&\displaystyle {\frac {\ell _{i}^{2}}{105}}&\displaystyle {\frac {13{\ell _{i}}}{420}}&\displaystyle -{\frac {\ell _{i}^{2}}{140}}\\\displaystyle {\frac {9}{70}}&\displaystyle {\frac {13{\ell _{i}}}{420}}&\displaystyle {\frac {13}{35}}&\displaystyle -{\frac {11{\ell _{i}}}{210}}\\\displaystyle -{\frac {13{\ell _{i}}}{420}}&\displaystyle -{\frac {\ell _{i}^{2}}{140}}&\displaystyle -{\frac {11{\ell _{i}}}{210}}&\displaystyle {\frac {\ell _{i}^{2}}{105}}\end{pmatrix}}\cdot {\begin{pmatrix}{{\ddot {W}}_{i-1}}\\{{\ddot {\Phi }}_{i-1}}\\{{\ddot {W}}_{i}}\\{{\ddot {\Phi }}_{i}}\end{pmatrix}}$

... der Formänderungsenergie eines Finiten Elements

$\delta \Pi _{i}=\displaystyle \int _{\displaystyle \ell _{i}}E\,I\;w_{i}''\cdot \delta w_{i}''dx_{i}$

ist

$\delta \Pi _{i}=\left({{\mathit {\delta W}}_{i-1}},{{\mathit {\delta \Phi }}_{i-1}},{{\mathit {\delta W}}_{i}},{{\mathit {\delta \Phi }}_{i}}\right)\,\displaystyle {\frac {\mathit {EI}}{{\ell }_{i}^{3}}}\,{\begin{pmatrix}12&6\,{\ell _{i}}&-12&6\,{\ell _{i}}\\6\,{\ell _{i}}&4\,{\ell _{i}^{2}}&-6\,{\ell _{i}}&2\,{\ell _{i}^{2}}\\-12&-6\,{\ell _{i}}&12&-6\,{\ell _{i}}\\6\,{\ell _{i}}&2\,{\ell _{i}^{2}}&-6\,{\ell _{i}}&4\,{\ell _{i}^{2}}\end{pmatrix}}\,{\begin{pmatrix}{{W}_{i-1}}\\{{\Phi }_{i-1}}\\{{W}_{i}}\\{{\Phi }_{i}}\end{pmatrix}}$.

⚠ Drehrichtung der Koordinate $\Phi _{j}$:

Die Drehung in diesem Modell ist entgegen der Rotation um die y-Achse definiert. Ein anderer Drehsinn führt zu anderen Vorzeichen in den System-Matrizen.

---

Links

• ...

Literature

• ...