Gelöste Aufgaben/W8Zv: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Biege-Belastung]][[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Finite-Elemente-Methode]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
Zu den tabellierten [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzellast, doppeltgelenkige Lagerung|Standardlösungen für den Euler-Bernoulli-Blaken]] berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken: | |||
<onlyinclude> | |||
[[Datei:W8Zv-01.png|200px|left|mini|Caption]] | |||
Hier soll mit dem Ansatz mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] gearbeitet werden. | |||
Gesucht ist das Verschiebungsfeld ''w(x)'' im Vergleich von FEM und analytischer Lösung. | |||
</onlyinclude> | |||
Diese Aufgabe ist eng verwandt mit [[Gelöste Aufgaben/W8Zt|W8Zt]] und [[Gelöste Aufgaben/W8Zu|W8Zu]]. | |||
== Lösung mit Maxima == | |||
Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], sowie | |||
::<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | |||
ist die analytische Lösung: | |||
::<math>EI w(x) = \frac{\displaystyle F \ell^3}{\displaystyle 6}\left[ \beta \xi ( 1-\beta^2-\xi^2)+<\xi-\alpha>^3 \right]</math>. | |||
Bei dieser Lösung hat die [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinate]] ''x'' ihren Ursprung in ''A'' - wir verwenden unten einen anderen Ursprung! | |||
Mit den passenden Ansatzfunktionen berechnen wir eine Näherungslösung des Problems nach dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]]. | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Virtual Strain-Energy per Element | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Boundary Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solve | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process: Results | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process: Compare with Analytic Solution | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<table class="wikitable" style="background-color:white; float: left; margin-right:14px; | |||
"> | |||
<tr><th></th><th></th></tr> | |||
<tr><td></td><td></td></tr> | |||
</table> | |||
<hr/> | |||
'''Links''' | |||
* [[Gelöste Aufgaben/W8Zt|W8Zt]], [[Gelöste Aufgaben/W8Zu|W8Zu]] | |||
'''Literature''' | |||
* ... | |||
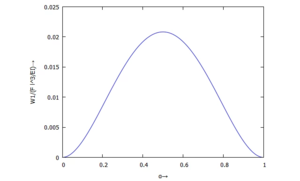
[[Datei:W8Zv-31.png|mini|Absenkung ''w(a)'' des Kraftangriffspunktes]] | [[Datei:W8Zv-31.png|mini|Absenkung ''w(a)'' des Kraftangriffspunktes]] | ||
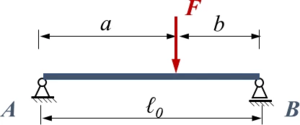
[[Datei:W8Zv-01.png|mini|Lageplan]] | [[Datei:W8Zv-01.png|mini|Lageplan]] | ||
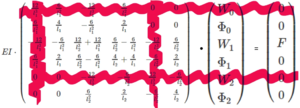
[[Datei:W8Zv-11.png|mini|Einarbeiten der Randbedingungen in die Systemmatrix]] | [[Datei:W8Zv-11.png|mini|Einarbeiten der Randbedingungen in die Systemmatrix]] | ||
Version vom 19. April 2021, 12:00 Uhr
Aufgabenstellung
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:
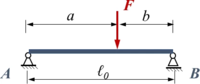
Hier soll mit dem Ansatz mit der Methode der Finiten Elemente gearbeitet werden. Gesucht ist das Verschiebungsfeld w(x) im Vergleich von FEM und analytischer Lösung.
Diese Aufgabe ist eng verwandt mit W8Zt und W8Zu.
Lösung mit Maxima
Mit dem Föppl-Symbol "<>", sowie
- , und
ist die analytische Lösung:
- .
Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!
Mit den passenden Ansatzfunktionen berechnen wir eine Näherungslösung des Problems nach dem Prinzip der virtuellen Verrückungen.
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Virtual Strain-Energy per Element
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Boundary Conditions
Text
1+1
tmp
Solve
Text
1+1
tmp
Post-Process: Results
Text
1+1
tmp
Post-Process: Compare with Analytic Solution
Text
1+1
Links
Literature
- ...