Gelöste Aufgaben/W8Zu: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Caption
(Die Seite wurde neu angelegt: „g“) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Prinzip vom Minimum der Potentiellen Energie]] | |||
[[Category:Biege-Belastung]][[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Rayleigh-Ritz-Prinzip]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
Zu den tabellierten [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzellast, doppeltgelenkige Lagerung|Standardlösungen für den Euler-Bernoulli-Blaken]] berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken: | |||
<onlyinclude> | |||
[[Datei:W8Zt-01.png|250px|left|mini|Caption]] | |||
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ryleigh-Ritz. | |||
</onlyinclude> | |||
Die Lösung nach einer Variante zu diesem Standardverfahren finden Sie hier in [[Gelöste Aufgaben/W8Zt|W8Zt]]. | |||
== Lösung mit Maxima == | |||
Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], sowie | |||
::<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | |||
ist die analytische Lösung: | |||
::<math>EI w(x) = \frac{\displaystyle F \ell^3}{\displaystyle 6}\left[ \beta \xi ( 1-\beta^2-\xi^2)+<\xi-\alpha>^3 \right]</math>. | |||
Bei dieser Lösung hat die [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinate]] ''x'' ihren Ursprung in ''A'' - wir verwenden unten einen anderen Ursprung! | |||
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems nach dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]]. | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Wir lösen das Problem mit [[Werkzeuge/Software/Maxima|Maxima]]. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
In Maxima treffen wir die Annahme ℓ>0, damit einige Integrale richtig gelöst werden. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solve | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Title | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process: Compare with Analytic Solution | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Version vom 19. April 2021, 10:15 Uhr
Aufgabenstellung
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:
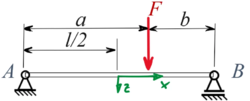
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ryleigh-Ritz.
Die Lösung nach einer Variante zu diesem Standardverfahren finden Sie hier in W8Zt.
Lösung mit Maxima
Mit dem Föppl-Symbol "<>", sowie
- , und
ist die analytische Lösung:
- .
![{\displaystyle EIw(x)={\frac {\displaystyle F\ell ^{3}}{\displaystyle 6}}\left[\beta \xi (1-\beta ^{2}-\xi ^{2})+<\xi -\alpha >^{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cf5956eaa1f4aff591ae6f755dced683f991b78)
Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems nach dem Prinzip vom Minimum der Potentiellen Energie.
tmp
Header
Wir lösen das Problem mit Maxima.
1+1
tmp
Declarations
In Maxima treffen wir die Annahme ℓ>0, damit einige Integrale richtig gelöst werden.
1+1
tmp
Formfunctions
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solve
Text
1+1
tmp
Post-Process
Text
1+1
tmp
Title
Text
1+1
tmp
Post-Process: Compare with Analytic Solution
Text
1+1
Links
- ...
Literature
- ...