Gelöste Aufgaben/W8Zt: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 19: | Zeile 19: | ||
Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], | Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], | ||
<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | ::<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | ||
ist die analytische Lösung: | ist die analytische Lösung: | ||
<math>EI w(x) = \frac{\displaystyle F \ell^3}{\displaystyle 6}\left[ \beta \xi ( 1-\beta^2-\xi^2)+<\xi-\alpha>^3 \right]</math>. | ::<math>EI w(x) = \frac{\displaystyle F \ell^3}{\displaystyle 6}\left[ \beta \xi ( 1-\beta^2-\xi^2)+<\xi-\alpha>^3 \right]</math>. | ||
Bei dieser Lösung hat die [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinate]] ''x'' ihren Ursprung in ''A'' - wir verwenden unten einen anderen Ursprung! | Bei dieser Lösung hat die [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinate]] ''x'' ihren Ursprung in ''A'' - wir verwenden unten einen anderen Ursprung! | ||
| Zeile 29: | Zeile 29: | ||
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems. | Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems. | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Hier arbeiten wir mit [[Werkzeuge/Software/Maxima|Maxima]]. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-09-14 */ | |||
/* ref: TM-C, Labor 3 - aus Gross, Augf. TM 2,Biegestab*/ | |||
/* description: finds the approx. solution employing */ | |||
/* two polynomial trialfunctions */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir definieren zunächst die Symbole für die virtuellen Arbeiten und die virtuellen Verrückungen - die in Maxima nicht standardmäßig verfügbar sind. | Wir definieren zunächst die Symbole für die virtuellen Arbeiten und die virtuellen Verrückungen - die in Maxima nicht standardmäßig verfügbar sind. | ||
Die Annahme ''ℓ>0'' brauchen wir, damit Maxima Wurzel-Ausdrücke mit diesem Parameter richtig vereinfachen kann. | Die Annahme ''ℓ>0'' brauchen wir, damit Maxima Wurzel-Ausdrücke mit diesem Parameter richtig vereinfachen kann. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/* declare variational variables - see 6.3 Identifiers */ | |||
declare("δW", alphabetic); | |||
declare("δA", alphabetic); | |||
declare("δΠ", alphabetic); | |||
declare("δV", alphabetic); | |||
declare("δΨ", alphabetic); | |||
declare("δw", alphabetic); | |||
/* declarations */ | |||
assume(l>0); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
Als [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinaten]] des Balkens wählen wir "''x''" entlang der Neutralen Faser mit Ursprung in der Mitte zwischen A und B. | {{MyCodeBlock|title=Formfunctions | ||
|text= | |||
Als [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinaten]] des Balkens wählen wir "''x''" entlang der [[Sources/Lexikon/Euler-Bernoulli-Balken/Neutrale Faser|Neutralen Faser]] mit Ursprung in der Mitte zwischen A und B. | |||
Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems und deren Variationen (''δ'') | Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems und deren Variationen (''δ'') | ||
<math> | ::<math> | ||
\underline{Q} = \left(\begin{array}{c}V\\\Psi\end{array}\right), \delta\underline{Q} = \left(\begin{array}{c}\delta V\\\delta \Psi\end{array}\right), </math> | \underline{Q} = \left(\begin{array}{c}V\\\Psi\end{array}\right), \delta\underline{Q} = \left(\begin{array}{c}\delta V\\\delta \Psi\end{array}\right), </math> | ||
[[Datei:W8Zt-11.png|mini|Koordinaten]] | |||
und wählen ''V'' und ''ψ'' als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt ''x''=0 des Balkens. | und wählen ''V'' und ''ψ'' als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt ''x''=0 des Balkens. | ||
| Zeile 84: | Zeile 101: | ||
mit der Lösung | mit der Lösung | ||
<math>{{c}_{1,0}}=V,{{c}_{1,2}}=-\frac{\displaystyle 4\cdot V}{{{\displaystyle \ell}^{2}}},{{c}_{2,1}}=\Psi,{{c}_{2,3}}=-\frac{\displaystyle 4\cdot \Psi}{\displaystyle {{\ell}^{2}}}</math> | ::<math>{{c}_{1,0}}=V,{{c}_{1,2}}=-\frac{\displaystyle 4\cdot V}{{{\displaystyle \ell}^{2}}},{{c}_{2,1}}=\Psi,{{c}_{2,3}}=-\frac{\displaystyle 4\cdot \Psi}{\displaystyle {{\ell}^{2}}}</math> | ||
Anstatt der exakten, bekannten Lösung, verwenden wir in diesem Näherungsansatz also nun die Funktion | |||
::<math>\mathrm{w}\left( x\right) =-\frac{\displaystyle 4\cdot {{x}^{2}}\cdot V}{{\displaystyle {\ell}^{2}}}+V-\frac{\displaystyle 4\cdot \Psi\cdot {{x}^{3}}}{{\displaystyle {\ell}^{2}}}+\Psi\cdot x</math>, | |||
[[Datei:W8Zt-12.png|mini|Trial-Functions]]die beiden Koordinaten ''V'' und ''ψ'' müssen wir noch bestimmen. Die Funktionen, die zu ''V'' und ''ψ'' gehören, sind rechts aufgetragen: | |||
Klar ist: die exakte Lösung dieses Lastfalls ist eine Funktion, die im [[Sources/Lexikon/Querkraftverlauf|Querkraftverlauf]] am Kraftangriffspunkt (''x=a - ℓ/2'') einen Sprung hat. Dagegen ist der Querkraftverlauf unserer Näherungslösung stetig differenzierbar und obendrauf noch konstant! | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
| Zeile 178: | Zeile 193: | ||
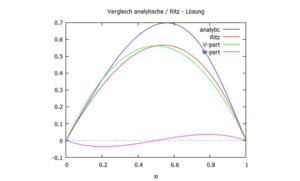
Und wir schauen uns für ''α=1/2'' die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an: | Und wir schauen uns für ''α=1/2'' die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an: | ||
[[Datei:W8Zt-32.png|mini|none|Vergleich der Biegelinie für analytische / numerische Lösung]] | [[Datei:W8Zt-32.png|mini|none|Vergleich der Biegelinie für analytische / numerische Lösung]] | ||
{{MyTip|title=Und wissen Sie auch ...|text=... wie der Verlauf der Querkraft im Vergleich Ritz / analytisch aussieht?}} | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
| Zeile 185: | Zeile 202: | ||
<hr/> | |||
<'''Links''' | <'''Links''' | ||
* ... | * ... | ||
| Zeile 191: | Zeile 208: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Version vom 19. April 2021, 09:59 Uhr
Aufgabenstellung
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:
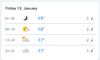
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten.
Üblich ist bei Verfahren von Rayleigh-Ritz nämlich sonst das Prinzip vom Minimum der Potentiellen Energie.
Lösung mit Maxima
Mit dem Föppl-Symbol "<>",
- , und
ist die analytische Lösung:
- .
Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems.
Header
Hier arbeiten wir mit Maxima.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-09-14 */
/* ref: TM-C, Labor 3 - aus Gross, Augf. TM 2,Biegestab*/
/* description: finds the approx. solution employing */
/* two polynomial trialfunctions */
/*******************************************************/
Declarations
Wir definieren zunächst die Symbole für die virtuellen Arbeiten und die virtuellen Verrückungen - die in Maxima nicht standardmäßig verfügbar sind.
Die Annahme ℓ>0 brauchen wir, damit Maxima Wurzel-Ausdrücke mit diesem Parameter richtig vereinfachen kann.
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δV", alphabetic);
declare("δΨ", alphabetic);
declare("δw", alphabetic);
/* declarations */
assume(l>0);
Formfunctions
Als unabhängige Koordinaten des Balkens wählen wir "x" entlang der Neutralen Faser mit Ursprung in der Mitte zwischen A und B.
Wir entscheiden uns zunächst für zwei abhängige Koordinaten des Systems und deren Variationen (δ)
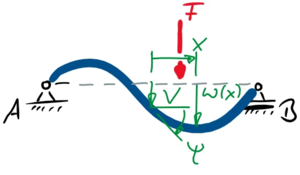
und wählen V und ψ als die Verschiebung und Verdrehung (=Neigung) des Querschnitts im Punkt x=0 des Balkens.
Jetzt brauchen wir zwei Ansatzfunktionen, die unseren Koordinaten V und ψ entsprechen. Wir wollen diese beiden anschaulich denken können - wir wählen einfache Polynome: eine achsensymmetrische und eine punktsymmetrische Funktion mit den noch unbestimmten Konstanten cij:
Diese beiden Funktionen müssen
- Geometrische Randbedingungen erfüllen und
- jeweils mit den Koordinaten V und ψ verknüpft werden.
Die zugehörigen Gleichungen (= die Randbedingungen) sind
- und
mit der Lösung
Anstatt der exakten, bekannten Lösung, verwenden wir in diesem Näherungsansatz also nun die Funktion
- ,
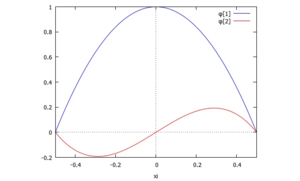
die beiden Koordinaten V und ψ müssen wir noch bestimmen. Die Funktionen, die zu V und ψ gehören, sind rechts aufgetragen:
Klar ist: die exakte Lösung dieses Lastfalls ist eine Funktion, die im Querkraftverlauf am Kraftangriffspunkt (x=a - ℓ/2) einen Sprung hat. Dagegen ist der Querkraftverlauf unserer Näherungslösung stetig differenzierbar und obendrauf noch konstant!
1+1
tmp
Mit dem Prinzip der virtuellen Verrückungen ist die Gleichgewichtsbedingung immer
Mit den Beiträgen
und dem Einsetzen der Ansatzfunktionen und deren Variation finden wir
Achtung: hier bezeichnet nun α=-1 den Punkt A, α=+1 den Punkt B.
Diese virtuelle Arbeit des Gesamtsystems spalten wir jetzt nach den virtuellen Verrückungen auf und erhalten zwei unabhängige Gleichungen in V und ψ:
Und die können wir leicht lösen:
Equilibrium Conditions
Text
1+1
tmp
In Matrix-Schreibweise stellen wir diesen Ausdruck gewöhnliches lineares Gleichungssystem dar:
mit
sieht das Gleichungssystem wieder handlich aus, die Lösung ist:
| ⚠ Und wissen Sie auch ....: |
| ... warum A hier eine Diagonalmatrix ist? Schauen Sie sich die Koeffizienten bzgl. von α an - was erkennen Sie? |
Solve
Text
1+1
tmp
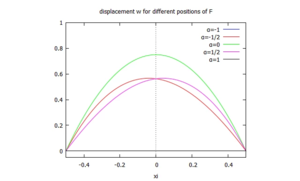
Die Lösung normieren wir noch für das Post-Processing mit der analytischen maximalen Auslenkung im symmetrischen Belastungsfall (wenn F in der Mitte zwischen A und B angreift):
Wir tragen sie für verschiedene Kraft-Angriffspunkte (α=-1,...α=+1) auf:
Post-Process
Text
1+1
Post-Process - Vergleich mit analytischer Lösung
Und wir schauen uns für α=1/2 die Verschiebung der Ritz- und analytischen-Lösung im Vergleich an:
| ✔ Und wissen Sie auch ...: |
| ... wie der Verlauf der Querkraft im Vergleich Ritz / analytisch aussieht? |
1+1
<Links
- ...
Literature
- ...