Gelöste Aufgaben/W8Zt: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 17: | Zeile 17: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Mit dem [[Sources/Lexikon/Föppl-Symbol|Föppl-Symbol "<>"]], | |||
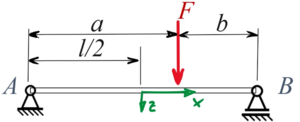
<math>\alpha = a/\ell</math>, <math>\beta = 1-\alpha</math> und <math>\xi = x/\ell</math> | |||
ist die analytische Lösung: | |||
<math>EI w(x) = \frac{\displaystyle F \ell^3}{\displaystyle 6}\left[ \beta \xi ( 1-\beta^2-\xi^2)+<\xi-\alpha>^3 \right]</math>. | |||
Bei dieser Lösung hat die [[Sources/Lexikon/unabhängige Koordinaten|unabhängige Koordinate]] ''x'' ihren Ursprung in ''A'' - wir verwenden unten einen anderen Ursprung! | |||
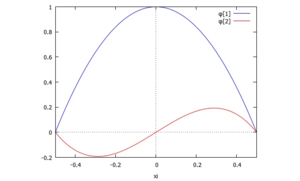
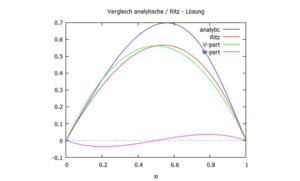
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems. | |||
==tmp== | ==tmp== | ||
Version vom 19. April 2021, 09:19 Uhr
Aufgabenstellung
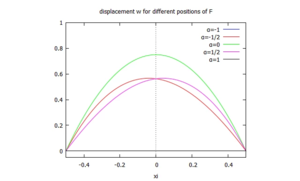
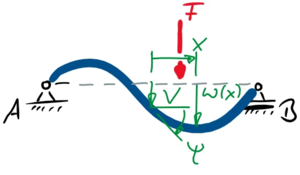
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten.
Üblich ist bei Verfahren von Rayleigh-Ritz nämlich sonst das Prinzip vom Minimum der Potentiellen Energie.
Lösung mit Maxima
Mit dem Föppl-Symbol "<>",
, und
ist die analytische Lösung:
.
Bei dieser Lösung hat die unabhängige Koordinate x ihren Ursprung in A - wir verwenden unten einen anderen Ursprung!
Mit den passenden Ansatzfunktionen nach Ritz berechnen Sie eine Näherungslösung des Problems.
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Formfunctions
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solve
Text
1+1
tmp
Post-Process
Text
1+1
<Links
- ...
Literature
- ...