Gelöste Aufgaben/W8Zt: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Caption
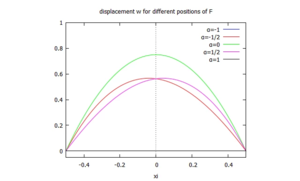
Parameterstudie: Auslenkung w(a) des Kraft-Einleitungspunktes 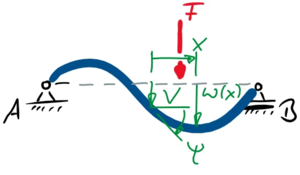
Koordinaten 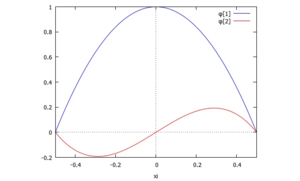
Trial-Functions 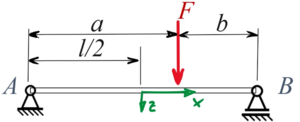
Lageplan 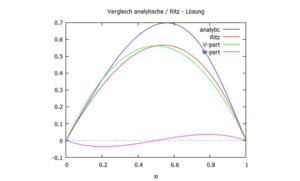
Vergleich der Biegelinie für analytische / numerische Lösung
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Prinzip der virtuellen Verrückungen]] | |||
[[Category:Biege-Belastung]][[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Rayleigh-Ritz-Prinzip]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
Zu den tabellierten [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzellast, doppeltgelenkige Lagerung|Standardlösungen für den Euler-Bernoulli-Blaken]] berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken: | |||
<onlyinclude> | |||
[[Datei:Screenshot 20210111-063733~2.png|100px|left|mini|Caption]] | |||
Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten. | |||
</onlyinclude> | |||
Üblich ist bei [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Im Vergleich: das Verfahren von Ritz und die Methode der Finite Elemente|Verfahren von Rayleigh-Ritz]] nämlich sonst das [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]]. | |||
== Lösung mit Maxima == | |||
Lorem Ipsum .... | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solve | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Process | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
<'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
[[Datei:W8Zt-31.png|mini|Parameterstudie: Auslenkung ''w(a)'' des Kraft-Einleitungspunktes]] | [[Datei:W8Zt-31.png|mini|Parameterstudie: Auslenkung ''w(a)'' des Kraft-Einleitungspunktes]] | ||
[[Datei:W8Zt-11.png|mini|Koordinaten]] | [[Datei:W8Zt-11.png|mini|Koordinaten]] | ||
Version vom 19. April 2021, 09:16 Uhr
Aufgabenstellung
Zu den tabellierten Standardlösungen für den Euler-Bernoulli-Blaken berechnen wir eine Näherungslösung für einen beidseitig gelenkig gelagerten Euler-Bernoulli-Balken:

Gesucht ist eine Lösung in Anlehnung an das Verfahren von Ritz - bei dem wir mit Formfunktionen arbeiten, die sich über die gesamte Balkenlänge erstrecken, wir aber im dann mit dem Prinzip der virtuellen Verrückungen arbeiten.
Üblich ist bei Verfahren von Rayleigh-Ritz nämlich sonst das Prinzip vom Minimum der Potentiellen Energie.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Formfunctions
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solve
Text
1+1
tmp
Post-Process
Text
1+1
<Links
- ...
Literature
- ...




