Gelöste Aufgaben/UEBP

Aufgabenstellung

Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.

Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet. 

Lageplan

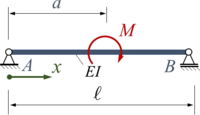
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.

Im Vergleich zu UEBO, das die gleiche Aufgabenstellung hat - arbeiten wir hier mit Ansatzfunktionen in zwei Sektionen wie bei der FEM. Nur das Gleichgewichts-Prinzip bliebt das Gleicht: das Prinzip vom Minimum der Potentiellen Energie.

Lösung mit Maxima

Beim Verfahren von Ritz arbeiten wir mit

• dem Prinzip vom Minimum der Potentiellen Energie.

Statt mit

• Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir
• hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen.

Header

Wir berechnen die Potentielle Energie U des Systems in Abhängigkeit von den generalisierten Koordinaten Wi und erhalten aus 

$\frac{dU}{d{W}_i}\stackrel{!}{=}0$

die Gleichung für den gesuchten Koeffizienten Wi der Trial-Funktionen.

📑 toggle code

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2019-10-19                            */
/* ref: TMC, Labor 3                                   */
/* description: Ritz / FEM approach to EBB, load-case 5*/
/*                                                     */
/*******************************************************/

/* declare variables and functions */
declare("Π", alphabetic); /* strain energy */
declare("ℓ", alphabetic); 
assume(ℓ>0);
dimless:[x=xi*ℓ,
         a=alpha*ℓ];

Declarations

Um die Lösung dimensionslos zu machen, nutzen wir wieder die analytische Lösung des Problems  und

• $W^{max}=\frac{M{\ell }^2}{9\sqrt{3}\cdot EI}$: die maximale Auslenkung des Balkens für a=ℓ.

Dimensionslose Orts-Koordinaten sind

$\begin{array}{ll}x& =\xi \cdot \ell ,\\ a& =\alpha \cdot \ell .\end{array}$.

📑 toggle code

/*********************************************************/
/*analytic solution vgl. Euler-Bernoulli-Blaken/Standard-Lösungen#case5*/
analytic: w(xi) = M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2)
/*                                   foeppel-function         */
                       - 3*(if xi<alpha then 0 else xi-alpha)^2);
W[max] : M*ℓ^2/(9*sqrt(3)*EI);

Formfunctions

Dass wir in UEBO die Trial-Funktions ϕ über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente M(x) und letztlich auch für die Verschiebungen w(x) zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut.

Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch.

Die Sektions- (Element-) Längen sind dabei

• für Sektion I: ${\ell }_I=\alpha \cdot \ell$  und
• für Sektion II: ${\ell }_{II}=(1-\alpha )\cdot \ell$.

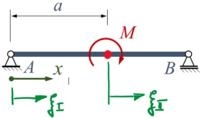Und wir arbeiten mit je einer Ortskoordinate ξ_i je Sektion, also

$0\le {\ell }_I\cdot {\xi }_I<a\text{ und }0\le {\ell }_{II}\cdot {\xi }_{II}<\ell -a$

mit

$0\le {\xi }_i<1$

Für die Trial-Functions wählen wir sektionsweise Polynome zweiten Grades

$\begin{array}{lcl}{w}_I({\xi }_I)& =& c_{1,2}\cdot {\xi }^2+c_{1,1}\cdot \xi +c_{1,0}\\ w_{II}({\xi }_{II)}& =& c_{2,2}\cdot {\xi }^2+c_{2,1}\cdot \xi +c_{2,0}\end{array}$,

deren Koeffizienten c_ij wir nun an die geometrischen Randbedingungen anpassen müssen:

$\begin{array}{lcl}{w}_I(0)& =& 0\\ w_I(1)& =& w_{II}(0)\\ {\frac{d{w}_I({\xi }_I)}{dx}|}_{\xi =1}& =& {\frac{d{w}_{II}({\xi }_{II})}{dx}|}_{\xi =0}\\ w_{II}(1)& =& 0\\ \end{array}$

Zusätzlich ersetzen wir zwei c_ij durch die Verschiebung und Verdrehung im Momenten-Einleitungspunkt

$\begin{array}{lcl}W& :=& w_{II}(0)\\ \mathrm{\Phi }& :=& {\frac{d{w}_{II}({\xi }_{II})}{dx}|}_{\xi =0}\end{array}$,

so dass die Trial-Functions die Form

$w(x)=\{\begin{array}{ccl}W\cdot {\varphi }_{1,1}({\xi }_I)& +\mathrm{\Phi }\cdot {\varphi }_{1,2}({\xi }_I)& \text{ für Sektion I}\\ W\cdot {\varphi }_{2,1}({\xi }_{II})& +\mathrm{\Phi }\cdot {\varphi }_{2,2}({\xi }_{II})& \text{ für Sektion II}\end{array}$

annehmen bzw.

$w(x)=\{\begin{array}{ccccl}W& \cdot (2\cdot {\xi }_I-{{\xi }_I}^2)& +\mathrm{\Phi }& \cdot (\alpha \cdot {{\xi }_I}^2-\alpha \cdot {\xi }_I)\cdot \ell & \text{ für }0<x<a,\\ W& \cdot (1-{{\xi }_{II}}^2)& +\mathrm{\Phi }& \cdot ((\alpha -1)\cdot {{\xi }_{II}}^2+(1-\alpha )\cdot {\xi }_{II})\cdot \ell & \text{ für }a<x<\ell .\end{array}$

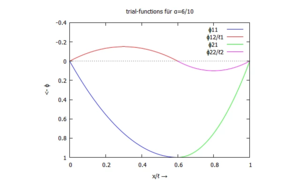
Im Plot sehen die vier Funktionen (zwei je Sektion,  zwei Sektionen) so aus:

Trial-Functions - wie bei der Methode der Finiten Elemente

📑 toggle code

/*********************************************************/
/* declare trial-function(s) */
ell : [alpha*ℓ,(1-alpha)*ℓ];
phi : makelist(sum(c[i,j]*xi^j,j,0,2),i,1,2);

/*********************************************************/
/* boundary-conditions for geometric boundary conditions */
GBC: [subst([xi = 0 ],      phi[1]           ) = 0,
      subst([xi = 1 ],      phi[1]           ) = subst([xi = 0 ],      phi[2]           ),
      subst([xi = 1 ],      phi[1]           ) = W,
      subst([xi = 1 ], diff(phi[1],xi)/ell[1]) = Phi,
      subst([xi = 1 ], diff(phi[1],xi)/ell[1]) = subst([xi = 0 ], diff(phi[2],xi)/ell[2]),
      subst([xi = 1 ],      phi[2]           ) = 0];

sol[1] : solve(GBC,[c[1,0],c[2,0],c[1,1],c[2,1],c[1,2],c[2,2]])[1];
phi: expand(ratsimp(subst(sol[1],phi)));

phi : ratsimp(makelist(makelist(coeff(phi[i],[W,Phi][j]),j,1,2),i,1,2));

/*********************************************************/
toPlot : [[parametric,          alpha *t, phi[1][1]  , [t,0,1]],
          [parametric,          alpha *t, phi[1][2]/ℓ, [t,0,1]],
          [parametric, alpha+(1-alpha)*t, phi[2][1]  , [t,0,1]],
          [parametric, alpha+(1-alpha)*t, phi[2][2]/ℓ, [t,0,1]]];
toPlot : subst([xi=t, alpha=6/10], toPlot);

preamble: "set yrange [] reverse";
plot2d(toPlot, [y,-0.4,1],
       [legend, "ϕ11   ","ϕ12/ℓ1","ϕ21   ","ϕ22/ℓ2"],
       [gnuplot_preamble, preamble],
       [title, "trial-functions für α=6/10"],
       [xlabel, "x/ℓ →"],
       [ylabel, "<- ϕ"] );

ansatz: makelist(w[i](xi) = sum(phi[i][j]*[W,Phi][j],j,1,2),i,1,2);

Potential Energy

Für die Gleichgewichtsbedingungen setzten wir Π (aus Abschnitt Euler-Bernoulli-Balken) und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir

$\frac{d\varphi }{x}=\frac{d\varphi }{{\xi }_i}\cdot \underset{=\frac{1}{{\ell }_i}}{\underbrace{\frac{d{\xi }_i}{x}}}$

berücksichtigen und erhalten mit der Arbeitsfunktion des Moments

$A=M\cdot w^{\prime }{|}_{x=a}$

das Potential in Matrix-Schreibweise:

$U=\frac{1}{2}\cdot {\underset{\_}{Q}}^T\cdot \underset{\_}{\underset{\_}{A}}\cdot \underset{\_}{Q}-{\underset{\_}{Q}}^T\cdot \underset{\_}{b}$.

wobei

$\underset{\_}{Q}=\left(\begin{array}{c}W\\ \mathrm{\Phi }\end{array}\right)$.

📑 toggle code

/*********************************************************/
/* define potential energy of system */
PMPE : [U = Π - A,
        Π = sum(1/2*EI/ell[i]^3*'integrate('diff(w[i](xi),xi,2)^2,xi,0,1),i,1,2),
        A = M*Phi];

PMPE: subst(ansatz, subst(PMPE[3],subst(PMPE[2], PMPE[1])));
PMPE : expand(ev(PMPE,nouns));

/* unknowns */
Q : [W,Phi];

Equilibrium Conditions

Diese Gleichung erfüllt die Gleichgewichtsbedingungen

$\frac{dU}{d{Q}_i}\stackrel{!}{=}0$,

wenn

$\left(\begin{array}{cc}-\frac{(4-12\cdot \alpha +12\cdot {\alpha }^2)\cdot EI}{({\alpha }^6-3\cdot {\alpha }^5+3\cdot {\alpha }^4-{\alpha }^3)\cdot {\ell }^3}& \frac{4(2\cdot \alpha -1)\cdot EI}{({\alpha }^4-2\cdot {\alpha }^3+{\alpha }^2)\cdot {\ell }^2}\\ 4\frac{(2\cdot \alpha -1)\cdot EI}{({\alpha }^4-2\cdot {\alpha }^3+{\alpha }^2)\cdot {\ell }^2}& -\frac{4\cdot EI}{({\alpha }^2-\alpha )\cdot \ell }\end{array}\right)\cdot \left(\begin{array}{c}W\\ \mathrm{\Phi }\end{array}\right)=\left(\begin{array}{c}0\\ M\end{array}\right)$.

Hier kann man schon am Gleichungssystem ablesen, was für α=½ passiert: dann werden die Nebendiagonal-Elemente mit Ihren (2 α-1)-Koeffizienten zu Null, dann ist

• $W=0$ und
• $\frac{16EI}{\ell }\mathrm{\Phi }=M$.

📑 toggle code

/* equilibrium condition */
eom : makelist(expand(diff(subst(PMPE,U),Q[i])),i,1,2);

A :   funmake('matrix, makelist(makelist(coeff(eom[i],Q[j]),j,1,2),i,1,2));
b : - funmake('matrix, makelist([subst(makelist(Q[j]=0,j,1,2),eom[i])],i,1,2));

print(A,"∙",transpose(Q),"=",b)$

Solving

Auflösen der Gleichungen nach den unbekannten Koordinaten W und Φ liefert

$\begin{array}{ll}W& =\frac{(\alpha -3\cdot {\alpha }^2+2\cdot {\alpha }^3)\cdot M\cdot {\ell }^2}{4\cdot EI}\\ \mathrm{\Phi }& =\frac{(1-3\cdot \alpha +3\cdot {\alpha }^2)\cdot M\cdot \ell }{4\cdot EI}\end{array}$.

Damit ist die gesuchte Näherungs-Lösung

$\begin{array}{ll}{w}_I({\xi }_I)& =\frac{(({\alpha }^3-3\cdot {\alpha }^2+\alpha )\cdot \xi +{\alpha }^3\cdot {\xi }^2)\cdot M\cdot {\ell }^2}{4\cdot EI}\\ w_{II}({\xi }_{II})& =\frac{(\alpha -3\cdot {\alpha }^2+2\cdot {\alpha }^3+(-3\cdot {\alpha }^3+6\cdot {\alpha }^2-4\cdot \alpha +1)\cdot \xi +({\alpha }^3-3\cdot {\alpha }^2+3\cdot \alpha -1)\cdot {\xi }^2)\cdot M\cdot {\ell }^2}{4\cdot EI}\end{array}$.

📑 toggle code

/*********************************************************/
/* solve */
sol[2] : ratsimp(solve(eom,Q))[1];
/* approximated solution */
ritz : ratsimp(subst(sol[2],ansatz));

Post-Processing

Verläufe von w(x), ϕ(x)

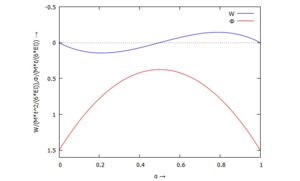
Die gesuchten Koordinaten  W und Φ tragen wir über α auf:

Wir lesen ab:

• für α=½: die Lösung wird - wie erwartet - nur durch ϕ₂ beschreiben - also W = 0.
• für α= 0: die Lösung wird - wie erwartet - nur durch ϕ₂ beschreiben - also W = 0.

Im Plot der normierten Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung - hier nur für a = ℓ/2 - zeigt sich, dass die Lösung von deutlich besserer Qualität ist:

Vergleich analytische / numerische Lösung für w(x)

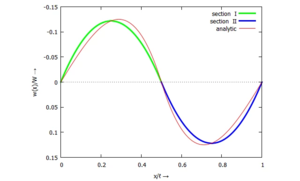
Während in UEBO die Näherungslösung gerade mal 1/4 der analytischen Lösung erreichte, haben wir hier fast die gleichen Auslenkungen. Und das, obwohl die Modelle hier und in UEBO jeweils nur zwei Unbekannte haben.

📑 toggle code

/*********************************************************/
/* post-processing */

/* plot "weights" W, Φ over a */
plot2d([subst(sol[2],W)/(M*ℓ^2/(6*EI)),subst(sol[2],Phi)/(M*ℓ/(6*EI))],[alpha,0,1],
  [y,-0.5,1.6],
  [legend, "W", "Φ"],
  [xlabel, "α →"],
  [ylabel, "W/(M*ℓ^2/(6*EI)),Φ/(M*ℓ/(6*EI)) →"] );

/* plot y-axis upside-down */
preamble: "set yrange [] reverse";

/* plot displacement w(x) for α = 1/2 */
toPlot : subst([xi=t, alpha=1/2],[[parametric,          alpha *t, ratsimp(subst( ritz,w[1](xi))/W[max]),[t,0,1]],
                                  [parametric, alpha+(1-alpha)*t, ratsimp(subst( ritz,w[2](xi))/W[max]),[t,0,1]],
                                  [parametric,                 t, ratsimp(subst(analytic,w(xi))/W[max]),[t,0,1]]]);

plot2d(toPlot,
  [legend, "section  I", "section  II", "analytic"],
  [color, green, blue, red],
  [style, [lines,3], [lines,3], [lines,1]],
  [gnuplot_preamble, preamble],
  [xlabel, "x/ℓ →"],
  [ylabel, "w(x)/W →"] );

Post-Processing - Nachtrag

Wir schauen uns auch hier wie in UEBO den Vergleich von Näherungslösung - hier nur für α=½ - und der analytischen Lösung des Biegemomenten-Verlaufs an:

Vergleich analytische / numerische Lösung für das Schnittmoment M(x)

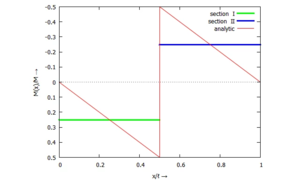
Durch das Ansetzen mit zwei separaten Ansatzfunktionen - je eine je Sektion - können wir nun den Sprung im Verlauf der Biegemomente abbilden. Und das macht die Lösung so viel genauer!

📑 toggle code

/* plot moments My(x) for α = 1/2 */
toPlot : subst([xi=t, alpha=1/2],[[parametric,          alpha *t, EI*diff(ratsimp(subst( ritz,w[1](xi))/M),xi,2)/ell[1]^2,[t,0,1]],
                                  [parametric, alpha+(1-alpha)*t, EI*diff(ratsimp(subst( ritz,w[2](xi))/M),xi,2)/ell[1]^2,[t,0,1]],
                                  [parametric,                 t, EI*M*ℓ^2/(6*EI)*ratsimp((6*xi-3*(if xi<alpha then 0 else 2))/ℓ^2/M),[t,0,1]]]);

plot2d(toPlot,
  [legend, "section  I", "section  II", "analytic"],
  [color, green, blue, red],
  [style, [lines,3], [lines,3], [lines,1]],
  [gnuplot_preamble, preamble],
  [xlabel, "x/ℓ →"],
  [ylabel, "M(x)/M →"] );