Gelöste Aufgaben/UEBP

Aufgabenstellung

Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.

Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet. 

Lageplan

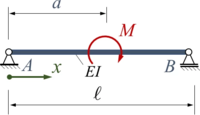
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.

Im Vergleich zu UEBO, das die gleiche Aufgabenstellung hat - arbeiten wir hier mit Ansatzfunktionen in zwei Sektionen wie bei der FEM. Nur das Gleichgewichts-Prinzip bliebt das Gleicht: das Prinzip vom Minimum der Potentiellen Energie.

Lösung mit Maxima

Beim Verfahren von Ritz arbeiten wir mit

• dem Prinzip vom Minimum der Potentiellen Energie.

Statt mit

• Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir
• hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen.

tmp

Header

Text

1+1

tmp

Um die Lösung dimensionslos zu machen, nutzen wir wieder die analytische Lösung des Problems  und

• $W^{max}=\displaystyle {\frac {M\,\ell ^{2}}{9{\sqrt {3}}\,\cdot E\,I}}$: die maximale Auslenkung des Balkens für a=ℓ.

Dimensionslose Orts-Koordinaten sind

${\begin{array}{ll}x&=\xi \cdot \ell ,\\a&=\alpha \cdot \ell .\end{array}}$.

Declarations

Text

1+1

tmp

Dass wir in UEBO die Trial-Funktions ϕ über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente M(x) und letztlich auch für die Verschiebungen w(x) zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut.

Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch.

Die Sektions- (Element-) Längen sind dabei

• für Sektion I: $\ell _{I}=\alpha \cdot \ell$  und
• für Sektion II: $\ell _{II}=(1-\alpha )\cdot \ell$.

Unabhängige Koordinaten der Finiten Elemente

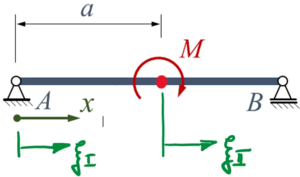
Und wir arbeiten mit je einer Ortskoordinate ξ_i je Sektion, also

$0\leq \ell _{I}\cdot \xi _{I}<a{\text{ und }}0\leq \ell _{II}\cdot \xi _{II}<\ell -a$

mit

$0\leq \xi _{i}<1$

Für die Trial-Functions wählen wir sektionsweise Polynome zweiten Grades

${\begin{array}{lcl}w_{I}(\xi _{I})&=&c_{1,2}\cdot \xi ^{2}+c_{1,1}\cdot \xi +c_{1,0}\\w_{II}(\xi _{II)}&=&c_{2,2}\cdot \xi ^{2}+c_{2,1}\cdot \xi +c_{2,0}\end{array}}$,

deren Koeffizienten c_ij wir nun an die geometrischen Randbedingungen anpassen müssen:

${\begin{array}{lcl}w_{I}(0)&=&0\\w_{I}(1)&=&w_{II}(0)\\\left.\displaystyle {\frac {dw_{I}(\xi _{I})}{dx}}\right|_{\xi =1}&=&\left.\displaystyle {\frac {dw_{II}(\xi _{II})}{dx}}\right|_{\xi =0}\\w_{II}(1)&=&0\\\end{array}}$

Zusätzlich ersetzen wir zwei c_ij durch die Verschiebung und Verdrehung im Momenten-Einleitungspunkt

${\begin{array}{lcl}W&:=&w_{II}(0)\\\Phi &:=&\left.\displaystyle {\frac {dw_{II}(\xi _{II})}{dx}}\right|_{\xi =0}\end{array}}$,

so dass die Trial-Functions die Form

$w(x)=\left\{{\begin{array}{ccl}W\cdot \phi _{1,1}(\xi _{I})&+\Phi \cdot \phi _{1,2}(\xi _{I})&{\text{ für Sektion I}}\\W\cdot \phi _{2,1}(\xi _{II})&+\Phi \cdot \phi _{2,2}(\xi _{II})&{\text{ für Sektion II}}\end{array}}\right.$

annehmen bzw.

$w(x)=\left\{{\begin{array}{ccccl}W&\cdot \left(2\cdot \xi _{I}-{{\xi _{I}}^{2}}\right)&+\Phi &\cdot \left(\alpha \cdot {{\xi _{I}}^{2}}-\alpha \cdot \xi _{I}\right)\cdot \ell &{\text{ für }}0<x<a,\\W&\cdot \left(1-{{\xi _{II}}^{2}}\right)&+\Phi &\cdot \left(\left(\alpha -1\right)\cdot {{\xi _{II}}^{2}}+\left(1-\alpha \right)\cdot \xi _{II}\right)\cdot \ell &{\text{ für }}a<x<\ell .\end{array}}\right.$

Im Plot sehen die vier Funktionen (zwei je Sektion,  zwei Sektionen) so aus:

Trial-Functions - wie bei der Methode der Finiten Elemente

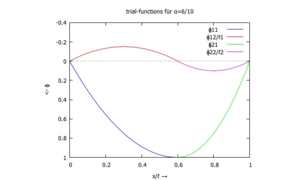
Formfunctions

Text

1+1

tmp

Für die Gleichgewichtsbedingungen setzten wir Π (aus Abschnitt Euler-Bernoulli-Balken) und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir

$\displaystyle {\frac {d\phi }{x}}={\frac {d\phi }{\xi _{i}}}\cdot \underbrace {\displaystyle {\frac {d\xi _{i}}{x}}} _{\displaystyle ={\frac {1}{\ell _{i}}}}$

berücksichtigen und erhalten mit der Arbeitsfunktion des Moments

$A=M\cdot w'|_{\displaystyle x=a}$

das Potential in Matrix-Schreibweise:

$U=\displaystyle {\frac {1}{2}}\cdot \displaystyle {\underline {Q}}^{T}\cdot {\underline {\underline {A}}}\cdot {\underline {Q}}-{\underline {Q}}^{T}\cdot {\underline {b}}$.

wobei

${\underline {Q}}=\left({\begin{array}{c}W\\\Phi \end{array}}\right)$.

Potential Energy

Text

1+1

tmp

Diese Gleichung erfüllt die Gleichgewichtsbedingungen

$\displaystyle {\frac {dU}{dQ_{i}}}{\stackrel {!}{=}}0$,

wenn

${\begin{pmatrix}-{\frac {\left(4-12\cdot \alpha +12\cdot {{\alpha }^{2}}\right)\cdot EI}{\left({{\alpha }^{6}}-3\cdot {{\alpha }^{5}}+3\cdot {{\alpha }^{4}}-{{\alpha }^{3}}\right)\cdot {{\ell }^{3}}}}&{\frac {4\left(2\cdot \alpha -1\right)\cdot EI}{\left({{\alpha }^{4}}-2\cdot {{\alpha }^{3}}+{{\alpha }^{2}}\right)\cdot {{\ell }^{2}}}}\\4{\frac {\left(2\cdot \alpha -1\right)\cdot EI}{\left({{\alpha }^{4}}-2\cdot {{\alpha }^{3}}+{{\alpha }^{2}}\right)\cdot {{\ell }^{2}}}}&-{\frac {4\cdot EI}{\left({{\alpha }^{2}}-\alpha \right)\cdot \ell }}\end{pmatrix}}\cdot {\begin{pmatrix}W\\\Phi \end{pmatrix}}={\begin{pmatrix}0\\M\end{pmatrix}}$.

Hier kann man schon am Gleichungssystem ablesen, was für α=½ passiert: dann werden die Nebendiagonal-Elemente mit Ihren (2 α-1)-Koeffizienten zu Null, dann ist

• $W=0$ und
• $\displaystyle {\frac {16EI}{\ell }}\Phi =M$.

Equilibrium Conditions

Text

1+1

tmp

Auflösen der Gleichungen nach den unbekannten Koordinaten W und Φ liefert

${\begin{array}{ll}W&=\displaystyle {\frac {\left(\alpha -3\cdot {{\alpha }^{2}}+2\cdot {{\alpha }^{3}}\right)\cdot M\cdot {{\ell }^{2}}}{4\cdot EI}}\\\Phi &=\displaystyle {\frac {\left(1-3\cdot \alpha +3\cdot {{\alpha }^{2}}\right)\cdot M\cdot \ell }{4\cdot EI}}\end{array}}$.

Damit ist die gesuchte Näherungs-Lösung

${\begin{array}{ll}w_{I}(\xi _{I})&={\frac {\left(\left({{\alpha }^{3}}-3\cdot {{\alpha }^{2}}+\alpha \right)\cdot \xi +{{\alpha }^{3}}\cdot {{\xi }^{2}}\right)\cdot M\cdot {{\ell }^{2}}}{4\cdot EI}}\\w_{II}(\xi _{II})&={\frac {\left(\alpha -3\cdot {{\alpha }^{2}}+2\cdot {{\alpha }^{3}}+\left(-3\cdot {{\alpha }^{3}}+6\cdot {{\alpha }^{2}}-4\cdot \alpha +1\right)\cdot \xi +\left({{\alpha }^{3}}-3\cdot {{\alpha }^{2}}+3\cdot \alpha -1\right)\cdot {{\xi }^{2}}\right)\cdot M\cdot {{\ell }^{2}}}{4\cdot EI}}\end{array}}$.

Solving

Text

1+1

tmp

Verläufe von w(x), ϕ(x)

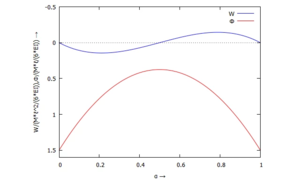
Die gesuchten Koordinaten  W und Φ tragen wir über α auf:

Wir lesen ab:

• für α=½: die Lösung wird - wie erwartet - nur durch ϕ₂ beschreiben - also W = 0.
• für α= 0: die Lösung wird - wie erwartet - nur durch ϕ₂ beschreiben - also W = 0.

Im Plot der normierten Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung - hier nur für a = ℓ/2 - zeigt sich, dass die Lösung von deutlich besserer Qualität ist:

Vergleich analytische / numerische Lösung für w(x)

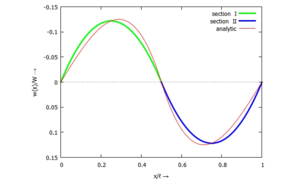
Während in UEBO die Näherungslösung gerade mal 1/4 der analytischen Lösung erreichte, haben wir hier fast die gleichen Auslenkungen. Und das, obwohl die Modelle hier und in UEBO jeweils nur zwei Unbekannte haben.

Vergleich analytische / numerische Lösung für das Schnittmoment M(x)

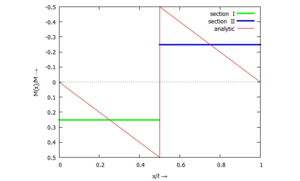
Post-Processing

Text

1+1