Gelöste Aufgaben/UEBP: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 69: | Zeile 69: | ||
* für Sektion II: <math>\ell_{II} = (1-\alpha) \cdot \ell</math>. | * für Sektion II: <math>\ell_{II} = (1-\alpha) \cdot \ell</math>. | ||
[[Datei:UEBP-11.png|rahmenlos]]<!--------------------------------------------------------------------------------> | [[Datei:UEBP-11.png|rahmenlos]] | ||
<!--------------------------------------------------------------------------------> | |||
| Zeile 79: | Zeile 81: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
==tmp== | ==tmp== | ||
Version vom 19. April 2021, 07:08 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
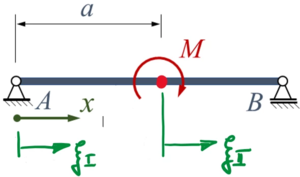
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
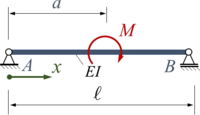
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
Im Vergleich zu UEBO, das die gleiche Aufgabenstellung hat - arbeiten wir hier mit Ansatzfunktionen in zwei Sektionen wie bei der FEM. Nur das Gleichgewichts-Prinzip bliebt das Gleicht: das Prinzip vom Minimum der Potentiellen Energie.
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
Statt mit
- Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir
- hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen.
tmp
Header
Text
1+1
tmp
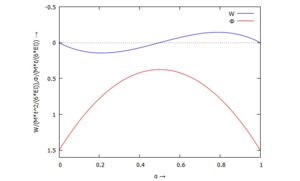
Um die Lösung dimensionslos zu machen, nutzen wir wieder die analytische Lösung des Problems und
- : die maximale Auslenkung des Balkens für a=ℓ.
Dimensionslose Orts-Koordinaten sind
.
Declarations
Text
1+1
tmp
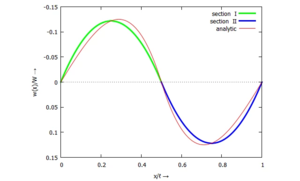
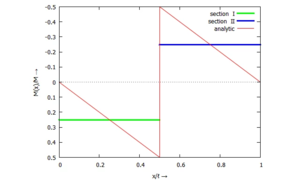
Dass wir in UEBO die Trial-Funktions ϕ über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente M(x) und letztlich auch für die Verschiebungen w(x) zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut.
Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch.
Die Sektions- (Element-) Längen sind dabei
- für Sektion I: und
- für Sektion II: .
Formfunctions
Text
1+1
tmp
Potential Energy
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1