Gelöste Aufgaben/UEBP: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 42: | Zeile 42: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Um die Lösung dimensionslos zu machen, nutzen wir wieder die [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzelmoment, doppeltgelenkige Lagerung|analytische Lösung des Problems]] und | ||
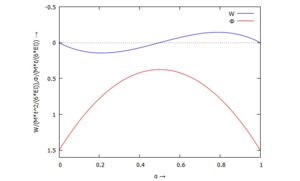
* <math>W^{max} = \displaystyle \frac{M\,\ell^2}{9\sqrt{3}\,\cdot E\,I}</math>: die maximale Auslenkung des Balkens für a=''ℓ.'' | |||
Dimensionslose Orts-Koordinaten sind | |||
<math>\begin{array}{ll} x &= \xi\cdot \ell,\\ a &= \alpha\cdot \ell. \end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 52: | Zeile 60: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Dass wir in [[Gelöste Aufgaben/UEBO|UEBO]] die Trial-Funktions ''ϕ'' über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente ''M(x)'' und letztlich auch für die Verschiebungen ''w(x)'' zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut. | ||
Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch. | |||
Die Sektions- (Element-) Längen sind dabei | |||
* für Sektion I: <math>\ell_I = \alpha \cdot \ell</math> und | |||
* für Sektion II: <math>\ell_{II} = (1-\alpha) \cdot \ell</math>. | |||
[[Datei:UEBP-11.png|rahmenlos]]<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
Version vom 19. April 2021, 07:07 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
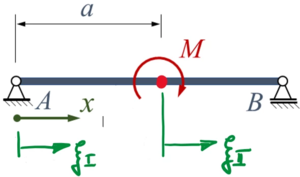
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
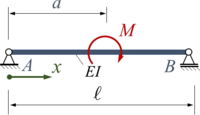
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
Im Vergleich zu UEBO, das die gleiche Aufgabenstellung hat - arbeiten wir hier mit Ansatzfunktionen in zwei Sektionen wie bei der FEM. Nur das Gleichgewichts-Prinzip bliebt das Gleicht: das Prinzip vom Minimum der Potentiellen Energie.
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
Statt mit
- Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir
- hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen.
tmp
Header
Text
1+1
tmp
Um die Lösung dimensionslos zu machen, nutzen wir wieder die analytische Lösung des Problems und
- : die maximale Auslenkung des Balkens für a=ℓ.
Dimensionslose Orts-Koordinaten sind
.
Declarations
Text
1+1
tmp
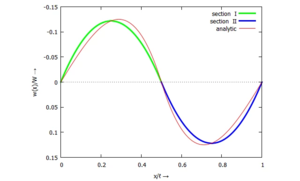
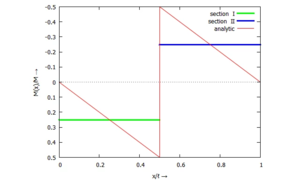
Dass wir in UEBO die Trial-Funktions ϕ über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente M(x) und letztlich auch für die Verschiebungen w(x) zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut.
Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch.
Die Sektions- (Element-) Längen sind dabei
- für Sektion I: und
- für Sektion II: .
Formfunctions
Text
1+1
tmp
Potential Energy
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1