Gelöste Aufgaben/UEBO: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 223: | Zeile 223: | ||
}} | }} | ||
Wieso die Näherungslösung - besonders für ''α=½'' - so schlecht ist, erkennt man beim Auftragen der Biegemomente im Stab für | |||
* die analytische Lösung | |||
<math>\displaystyle \frac{M(x)}{M} = \left\{ | |||
\begin{array}{cl} | |||
-\xi&\ldots\text{ für } \xi<\frac{1}{2}\\ | |||
1-\xi&\ldots\text{ sonst. } | |||
\end{array} | |||
\right.</math> und | |||
* die numerische Lösung | |||
<math>\displaystyle \frac{M(x)}{M} = \frac{1}{4} (2 \xi-1)</math>. | |||
{{MyCodeBlock|title=Post-Processing - Nachtrag | {{MyCodeBlock|title=Post-Processing - Nachtrag | ||
|text=Text | |text=Text | ||
Version vom 19. April 2021, 06:28 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
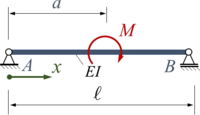
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
(Weg "1" wie in UEBH beschrieben.)
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
tmp
Wir berechnen die Potentielle Energie U des Systems in Abhängigkeit von den generalisierten Koordinaten Wi und erhalten aus
die Gleichung für den gesuchten Koeffizienten Wi der Trial-Funktionen.
Header
Text
1+1
tmp
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des Problems , hier die Beträge der maximalen Auslenkung des Balkens für a = ℓ und der Verdrehung des Balkens am Momenten-Angriffspunkt für a = ℓ/2:
die maximale Auslenkung des Balkens für a=ℓ
die Verdrehung des Balkens am Momenten-Angriffspunkt für a=ℓ/2
Dimensionslose Orts-Koordinaten sind
.
Declarations
Text
1+1
tmp
Bei der Suche nach passenden Trial-Functions ϕ lassen wir uns ebenfalls von der analytischen Lösung des Problems "inspirieren":
Der Funktionsverlauf von wa hat zwei charakteristische Ausprägungen:
Und so wählen wir unsere Trial-Functions als
.
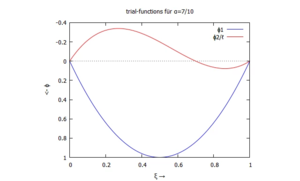
Für α=7∙ℓ/10 sehen sie so aus;
Die Koeffizienten c1 und c2 haben wir dabei so gewählt, dass
.
Mit den neuen, gesuchten Wichtungsfaktoren qw und qϕ ist die Ansatzfunktion zur Lösung mit dem Verfahren von Rayleigh-Ritz damit
Aufgrund der gewählten Skalierungsfaktoren erwarten wir als Ergebnis näherungsweise
- für α=½: qw ≈ 0 und qϕ ≈ 1,
- für α= 0: qw ≈ 1 und qϕ ≈ 0.
Formfunctions
Text
1+1
tmp
Für die Gleichgewichtsbedingungen setzten wir Π (aus Abschnitt Euler-Bernoulli-Balken) und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir
berücksichtigen und erhalten mit der Arbeitsfunktion des Moments
das Potential in Matrix-Schreibweise:
.
wobei
.
Einsetzen der Ansatzfunktion in die Formänderungsenergie und die Arbeitsfunktion liefert für die Matrizen A und b:
,
.
Potential Energy
Text
1+1
tmp
Diese Gleichung erfüllt die Gleichgewichtsbedingungen
,
wenn
.
Equilibrium Conditions
Text
1+1
tmp
Auflösen der Gleichungen nach den unbekannten Koordinaten qw und qϕ liefert
.
Damit ist die gesuchte Näherungs-Lösung
.
Solving
Text
1+1
tmp
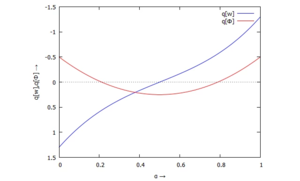
Die gesuchten Koordinaten qw und qΦ sind dimensionslos. Wir können sie direkt für verschiedene Werte von α auftragen.
Wir sehen:
- für α=½: die Lösung wird - wie erwartet - nur durch ϕ2 beschreiben - also qw ≈ 0 und qϕ ≈ 1; allerdings ist die Qualität der Lösung mit qϕ = 1/4 sehr schlecht - hier drückt der Sprung in der Momenten-Kennlinie der analytischen Lösung auf das Ergebnis (s.u.).
- für α= 0: die Lösung wird - wie erwartet - primär durch ϕ1 beschreiben, also qw ≈ 1 und qϕ ≈ 0. Hier zeigt die Lösung mit qw = 1.3 und qϕ = -0.5 einen recht großen Lösungs-Anteil der punktsymmetrischen Trial-Function.
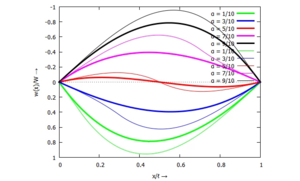
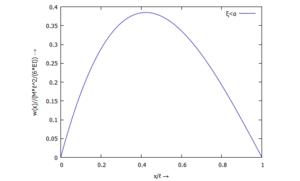
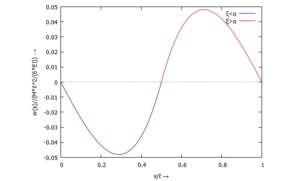
Und so sieht die normierte Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung für verschiedene Werte von a aus:
Die dicken Linien gehören zu Näherung nach dem Ritz-Ansatz, die dünnen zur analytischen Lösung. Je weiter der Momenten-Angriffspunkt in die Balken-Mitte rückt und besonders für α=1/2 liefert der Ritz-Ansatz kein überzeugendes Ergebnis. Hier müssten wir mehr Trial-Functions "spendieren".
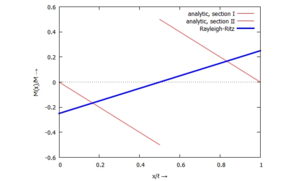
Post-Processing
Text
1+1
Wieso die Näherungslösung - besonders für α=½ - so schlecht ist, erkennt man beim Auftragen der Biegemomente im Stab für
- die analytische Lösung
und
- die numerische Lösung
.
Post-Processing - Nachtrag
Text
1+1
Links
- ...
Literature
- ...