Gelöste Aufgaben/UEBO: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
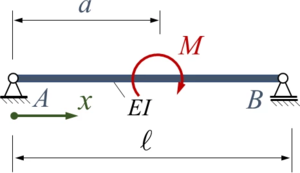
Lageplan
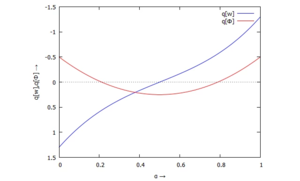
Verlauf der Koordinaten qw, qϕ 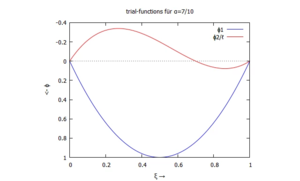
Trial-Functions 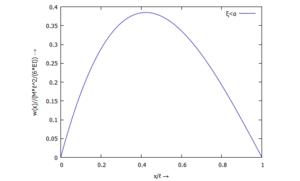
Biegelinie der Referenzlösung
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
Der Euler-Bernoulli-Balken ''AB'' wird durch ein Moment ''M'' zwischen den beiden gelenkigen Lagern belastet. | Der Euler-Bernoulli-Balken ''AB'' wird durch ein Moment ''M'' zwischen den beiden gelenkigen Lagern belastet. | ||
<onlyinclude> | <onlyinclude> | ||
| Zeile 23: | Zeile 20: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Beim Verfahren von Ritz arbeiten wir mit | Beim Verfahren von Ritz arbeiten wir mit | ||
| Zeile 33: | Zeile 29: | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Header | ||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 41: | Zeile 59: | ||
}} | }} | ||
==tmp== | |||
"> | |||
<!--------------------------------------------------------------------------------> | |||
< | {{MyCodeBlock|title=Potential Energy | ||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
Version vom 19. April 2021, 06:04 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.

Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
(Weg "1" wie in UEBH beschrieben.)
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Formfunctions
Text
1+1
tmp
Potential Energy
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
Links
- ...
Literature
- ...


