Gelöste Aufgaben/UEBL: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 7: | Zeile 7: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Die Problemstellung ist identisch zu [[Gelöste Aufgaben/UEBI|UEBI]] (und [[Gelöste Aufgaben/UEBJ|UEBJ]], [[Gelöste Aufgaben/UEBK|UEBK]]): | |||
<onlyinclude> | Der [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] ''AB'' wird durch seine Gewichtskraft belastet. Er ist in ''A'' fest eingespannt und hat eine konstante Breite ''b'' sowie eine zwischen ''A'' und ''B'' linear veränderliche Höhe ''h''.<onlyinclude> | ||
[[Datei:UEBF-01.png|250px|left|mini|Lageplan]] | [[Datei:UEBF-01.png|250px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist eine Näherungslösung mit der Methode der Finiten Elementen, die nur Elemente mit stückweise konstanten Querschnitts-Eigenschaften zulassen. | ||
</onlyinclude> | </onlyinclude> | ||
Gegeben sind für den Balken: | |||
* Länge ''ℓ'', Breite ''b,'' | |||
* E-Modul ''E'', Dichte ''ρ'' und | |||
* die Höhe ''h''<sub>0</sub>''=b'' und ''h<sub>1</sub>'' jeweils in ''A'' und ''B''; dazwischen ist die Höhe linear veränderlich. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
==tmp== | |||
Unsere [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/FEM: Trial-Functions für kubische Ansatz-Polynome|FEM-Formulierung mit kubischen Ansatz-Polynomen]] für [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] ist auf Stäbe mit elementweise konstantem Querschnitt beschränkt: ''E'' und ''I'' müssen je Element konstant sein. | |||
Für dieses Problem können wir die Formulierung also - nominell - nicht anwenden. Wir müssten im Abschnitt [[Sources/Lexikon/Virtuelle Formänderungsenergie|Virtuelle Formänderungsenergie]] die Integration für linear-veränderliche Querschnittsflächen ansetzen und durchführen. | |||
Das machen wir hier nicht.[[Datei:UEBL-11.png|mini|FE-Modell]]Wir schauen uns an, wie die Lösung für das Ersatz-Modell aussieht, bei dem wir uns den Originalstab durch einen stufenweise abgesetzten Stab ersetzt denken - hier für zwei Elemente. | |||
Die Querschnittseigenschaften je Element seien die des Original-Stabes im Element-Mittelpunkt.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 30: | Zeile 41: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir benutzen die Parameter-Deklarationen aus UEBI und laden außerdem die analytische Lösung von dort. | ||
Einziger Unterschied: um die Element-Länge ''ℓ<sub>i</sub>'' in Element "i" eindeutig von der Gesamt-Länge des Stabes zu unterscheiden, wählen wir für die Gesamt-Länge den Parameter ''ℓ<sub>0</sub>'' statt ''ℓ.''<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 41: | Zeile 56: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir verwenden aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken | ||
* die Standard Element-Steifigkeitsmatrix | |||
<math>\displaystyle \underline{\underline{K}}_i = \frac{E I_i}{\ell_i^3} \; | |||
\begin{pmatrix}12 & 6\cdot {{\ell}_{i}} & -12 & 6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}}\\ -12 & -6\cdot {{\ell}_{i}} & 12 & -6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}}\end{pmatrix}</math> | |||
* und die Element-"Rechte Seite " | |||
<math>\underline{P}_i = \rho\,A_i\,g\, \ell_i \cdot | |||
\begin{pmatrix}\displaystyle\frac{1}{2}\\ \displaystyle \frac{{{\ell}_{i}}}{12}\\ \displaystyle \frac{1}{2}\\ -\displaystyle \frac{{{\ell}_{i}}}{12}\end{pmatrix}</math>. | |||
Hier dürfen also der (mittlere) Querschnittsflächeninhalt ''A<sub>i</sub>'', das (mittlere) Flächenmoment ''I<sub>i</sub>'' und die Länge ''ℓ<sub>i</sub>'' je Element unterschiedliche Werte annehmen. | |||
Ab hier haben wir einige Freiheiten und die füllen wir folgendermaßen: | |||
* Die Anzahl der Finiten Element ist 3. | |||
* Die Element-Längen wählen wir so, dass sie sich in Stab-Längsrichtung verdoppeln, also | |||
<math>\ell_{i+1} = 2 \cdot \ell_i</math> | |||
Dann sind mit | |||
<math>\lambda_i := \ell_i/\ell_0</math> | |||
die relativen Element-Längen | |||
<math>\displaystyle {{\lambda}_{1}}=\frac{1}{7},{{\lambda}_{2}}=\frac{2}{7},{{\lambda}_{3}}=\frac{4}{7}</math>. | |||
Für diese drei Element bestimmen wir die "mid-point"-Querschnittseigenschaften zu | |||
<math>\displaystyle | |||
\tilde{A}_1 = \frac{\left( \frac{13\cdot {{h}_{0}}}{7}+\frac{{{h}_{1}}}{7}\right) \cdot b}{2}, | |||
\tilde{A}_2 = \frac{\left( \frac{10\cdot {{h}_{0}}}{7}+\frac{4\cdot {{h}_{1}}}{7}\right) \cdot b}{2}, | |||
\tilde{A}_3 = \frac{\left( \frac{4\cdot {{h}_{0}}}{7}+\frac{10\cdot {{h}_{1}}}{7}\right) \cdot b}{2}</math> | |||
und | |||
<math>\displaystyle | |||
\tilde{I}_1 = \frac{{{\left( \frac{13\cdot {{h}_{0}}}{7}+\frac{{{h}_{1}}}{7}\right) }^{3}}\cdot b}{96}, | |||
\tilde{I}_2 = \frac{{{\left( \frac{10\cdot {{h}_{0}}}{7}+\frac{4\cdot {{h}_{1}}}{7}\right) }^{3}}\cdot b}{96}, | |||
\tilde{I}_3 = \frac{{{\left( \frac{4\cdot {{h}_{0}}}{7}+\frac{10\cdot {{h}_{1}}}{7}\right) }^{3}}\cdot b}{96}</math> | |||
Einsetzen und komponieren der Gesamt-Systemmatrix - mit Einarbeiten der geometrischen Randbedingungen - liefert | |||
<math>\frac{{{b}^{4}}\cdot E}{{{\ell}_{0}^{3}}}\cdot | |||
\begin{pmatrix}\frac{21411}{64} & -\frac{16227\cdot {{\ell}_{0}}}{896} & -27 & \frac{27\cdot {{\ell}_{0}}}{7} & 0 & 0\\ -\frac{16227\cdot {{\ell}_{0}}}{896} & \frac{8865\cdot {{\ell}_{0}^{2}}}{3136} & -\frac{27\cdot {{\ell}_{0}}}{7} & \frac{18\cdot {{\ell}_{0}^{2}}}{49} & 0 & 0\\ -27 & -\frac{27\cdot {{\ell}_{0}}}{7} & \frac{14553}{512} & -\frac{6183\cdot {{\ell}_{0}}}{1792} & -\frac{729}{512} & \frac{729\cdot {{\ell}_{0}}}{1792}\\ \frac{27\cdot {{\ell}_{0}}}{7} & \frac{18\cdot {{\ell}_{0}^{2}}}{49} & -\frac{6183\cdot {{\ell}_{0}}}{1792} & \frac{1395\cdot {{\ell}_{0}^{2}}}{1568} & -\frac{729\cdot {{\ell}_{0}}}{1792} & \frac{243\cdot {{\ell}_{0}^{2}}}{3136}\\ 0 & 0 & -\frac{729}{512} & -\frac{729\cdot {{\ell}_{0}}}{1792} & \frac{729}{512} & -\frac{729\cdot {{\ell}_{0}}}{1792}\\ 0 & 0 & \frac{729\cdot {{\ell}_{0}}}{1792} & \frac{243\cdot {{\ell}_{0}^{2}}}{3136} & -\frac{729\cdot {{\ell}_{0}}}{1792} & \frac{243\cdot {{\ell}_{0}^{2}}}{1568}\end{pmatrix} | |||
\cdot \underline{Q} = | |||
m\,g\cdot \begin{pmatrix}\frac{25}{98}\\ \frac{23\cdot {{\ell}_{0}}}{4116}\\ \frac{20}{49}\\ \frac{16\cdot {{\ell}_{0}}}{1029}\\ \frac{12}{49}\\ -\frac{8\cdot {{\ell}_{0}}}{343}\end{pmatrix}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=FEM-Formulation | {{MyCodeBlock|title=FEM-Formulation | ||
|text=Text | |text=Text | ||
| Zeile 52: | Zeile 113: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Das lineare Gleichungssystem lösen wir mit der Referenz-Auslenkung | ||
<math>\displaystyle \hat{W} = \frac{q_{ref}\,\ell_0^4}{8\,E\,I_{ref}}</math> | |||
und | |||
<math>\displaystyle q_{ref} = \frac{m\,g}{\ell_0}, E\,I_{ref}=E\,b\,\frac{\left(\displaystyle \frac{h_0+h_1}{2}\right)^3}{12}</math> | |||
zu | |||
<math>\begin{array}{ccl} | |||
\displaystyle \frac{ W_0}{\hat{W}} &=& 0,\\ | |||
\displaystyle \frac{\Phi_0}{\hat{W}} &=& 0,\\ | |||
\displaystyle \frac{ W_1}{\hat{W}} &=& 0.016,\\ | |||
\displaystyle \frac{\Phi_1}{\hat{W}} &=& \displaystyle \frac{0.2093}{\ell_0},\\ | |||
\displaystyle \frac{ W_2}{\hat{W}} &=& 0.1317,\\ | |||
\displaystyle \frac{\Phi_2}{\hat{W}} &=& \displaystyle \frac{0.5545}{\ell_0},\\ | |||
\displaystyle \frac{ W_3}{\hat{W}} &=& 0.5937,\\ | |||
\displaystyle \frac{\Phi_3}{\hat{W}} &=& \displaystyle \frac{0.8932}{\ell_0} | |||
\end{array}</math> | |||
mit den Bezeichnungen nach Abschnitt [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/FEM: Trial-Functions für kubische Ansatz-Polynome|FEM: Trial-Functions für kubische Ansatz-Polynome]].<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 63: | Zeile 146: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Ergebnisse schauen wir uns als dimensionsloser Darstellung an, wobei wir wie in UEBI die Standard-Lösungen für den Balken unter konstanter Streckenlast als Referenz-Lösung ansetzen. | ||
Wir finden | |||
* ... für die Auslenkung ''w'':[[Datei:UEBL-31.png|mini|Biegelinie w(x)]] | |||
* ... für den Kippwinkel ''ϕ'':[[Datei:UEBL-32.png|mini|Kippwinkel ''ϕ(x)'']] | |||
* ... für das Biegemoment ''M'':[[Datei:UEBL-33.png|mini|Biegemomentenverlauf ''M(x)'']] | |||
* ... für die Querkraft ''Q'':[[Datei:UEBL-34.png|mini|Querkraftverlauf ''Q(x)'']]<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 85: | Zeile 177: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Version vom 19. April 2021, 05:31 Uhr
Aufgabenstellung
Die Problemstellung ist identisch zu UEBI (und UEBJ, UEBK):
Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.
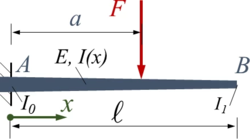
Gesucht ist eine Näherungslösung mit der Methode der Finiten Elementen, die nur Elemente mit stückweise konstanten Querschnitts-Eigenschaften zulassen.
Gegeben sind für den Balken:
- Länge ℓ, Breite b,
- E-Modul E, Dichte ρ und
- die Höhe h0=b und h1 jeweils in A und B; dazwischen ist die Höhe linear veränderlich.
Lösung mit Maxima
tmp
Unsere FEM-Formulierung mit kubischen Ansatz-Polynomen für Euler-Bernoulli-Balken ist auf Stäbe mit elementweise konstantem Querschnitt beschränkt: E und I müssen je Element konstant sein.
Für dieses Problem können wir die Formulierung also - nominell - nicht anwenden. Wir müssten im Abschnitt Virtuelle Formänderungsenergie die Integration für linear-veränderliche Querschnittsflächen ansetzen und durchführen.
Das machen wir hier nicht.

Wir schauen uns an, wie die Lösung für das Ersatz-Modell aussieht, bei dem wir uns den Originalstab durch einen stufenweise abgesetzten Stab ersetzt denken - hier für zwei Elemente.
Die Querschnittseigenschaften je Element seien die des Original-Stabes im Element-Mittelpunkt.
Header
Text
1+1
tmp
Wir benutzen die Parameter-Deklarationen aus UEBI und laden außerdem die analytische Lösung von dort.
Einziger Unterschied: um die Element-Länge ℓi in Element "i" eindeutig von der Gesamt-Länge des Stabes zu unterscheiden, wählen wir für die Gesamt-Länge den Parameter ℓ0 statt ℓ.
Declarations
Text
1+1
tmp
Wir verwenden aus Abschnitt FEM-Formulierung für den Euler-Bernoulli-Balken
- die Standard Element-Steifigkeitsmatrix
- und die Element-"Rechte Seite "
.
Hier dürfen also der (mittlere) Querschnittsflächeninhalt Ai, das (mittlere) Flächenmoment Ii und die Länge ℓi je Element unterschiedliche Werte annehmen.
Ab hier haben wir einige Freiheiten und die füllen wir folgendermaßen:
- Die Anzahl der Finiten Element ist 3.
- Die Element-Längen wählen wir so, dass sie sich in Stab-Längsrichtung verdoppeln, also
Dann sind mit
die relativen Element-Längen
.
Für diese drei Element bestimmen wir die "mid-point"-Querschnittseigenschaften zu
und
Einsetzen und komponieren der Gesamt-Systemmatrix - mit Einarbeiten der geometrischen Randbedingungen - liefert
.
FEM-Formulation
Text
1+1
tmp
Das lineare Gleichungssystem lösen wir mit der Referenz-Auslenkung
und
zu
mit den Bezeichnungen nach Abschnitt FEM: Trial-Functions für kubische Ansatz-Polynome.
Solving
Text
1+1
tmp
Die Ergebnisse schauen wir uns als dimensionsloser Darstellung an, wobei wir wie in UEBI die Standard-Lösungen für den Balken unter konstanter Streckenlast als Referenz-Lösung ansetzen.
Wir finden
- ... für die Auslenkung w:
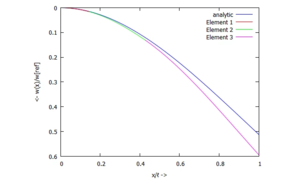
Biegelinie w(x) - ... für den Kippwinkel ϕ:
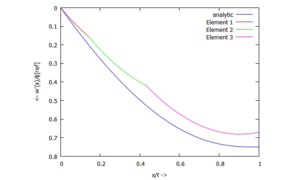
Kippwinkel ϕ(x) - ... für das Biegemoment M:
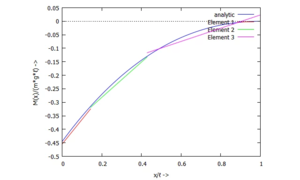
Biegemomentenverlauf M(x) - ... für die Querkraft Q:
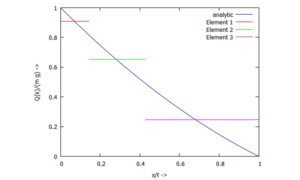
Querkraftverlauf Q(x)
Post-Processing
Text
1+1
Links
- ...
Literature
- ...