Gelöste Aufgaben/UEBJ: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 45: | Zeile 45: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | In diesem Problem werden wir Lösungen zu verschiedenen Ansatzfunktionen miteinander vergleichen. | ||
Es geht also nicht nur um die Berechnung einer Lösung - sondern vieler.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 56: | Zeile 59: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir arbeiten mit den System-Parametern | ||
<math>\begin{array}{lcl} | |||
\xi &=& \displaystyle \frac{x}{\ell},\\ | |||
q(\xi) &=& A(\xi)\,\rho\,g,\\ | |||
A(\xi) &=& b\,h(\xi),\\ | |||
I(\xi) &=& \displaystyle \frac{b\cdot h^3(\xi)}{12},\\ | |||
h(\xi) &=& h_0\cdot(1-\xi)+ h_1\cdot \xi \text{ und}\\ | |||
h_1 &=& \alpha \, h_0. | |||
\end{array}</math> | |||
Für die numerische Lösung verwenden wir - wie in [[Gelöste Aufgaben/UEBI|UEBI]] - | |||
<math>\alpha = \displaystyle \frac{1}{2}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 67: | Zeile 84: | ||
==tmp== | ==tmp== | ||
<!----------------------------- | Gesucht ist hier ein Ansatz mit polynomialen Trial Functions. Wir probieren verschiedene Ansätze aus, die wir mit "''i''" kennzeichnen, also | ||
{{MyCodeBlock|title=Rayleigh-Ritz Approach | |||
<math>w_i(\xi) = \hat{w} \cdot \displaystyle \sum_{j_{min}}^J W_{i,j} \cdot \phi_j(\xi)</math> | |||
und den gesuchten Koeffizienten ''W<sub>ij</sub>''. Die ''ϕ<sub>j</sub>'' müssen dabei alle geometrischen Randbedingungen erfüllen, also: | |||
<math>\begin{array}{ll}w_i(0) &= 0,\\w_i'(0) &= 0.\end{array}</math>. | |||
Die Funktionen müssen nicht die Randbedingungen für Schnittlasten in ''B'' erfüllen - schließlich suchen wir nach einer Näherungslösung! | |||
Diese Funktionen ''ϕ<sub>j</sub>'' zu konstruieren ist einfach: wir brauchen lediglich eine doppelte Nullstelle in <math>\xi=0</math>. Das erreichen wir, indem wir nur Polynome ab einem Grad ≥ 2 (also ''j<sub>min</sub>''=2) zulassen: | |||
<math>\phi_j(\xi) = \xi^j \text{ mit } j \ge 2</math>. | |||
Damit ist | |||
<math>w_i(\xi) = \hat{w} \cdot \displaystyle \sum_2^J W_{i,j} \cdot \xi^j</math>. | |||
Die freien Koeffizienten ''W<sub>ij</sub>'' sind nun die anteiligen Auslenkungen in ''B''. | |||
----Für die Gleichgewichtsbedingungen setzten wir die Formänderungsenergie '''''Π''''' (aus dem Abschnitt [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]]) | |||
<math>\displaystyle \Pi = \frac{1}{2} \int_0^\ell M(x)\,w''(x) dx</math> | |||
und die Arbeitsfunktion der Gewichtskraft '''''A''''' | |||
<math>\displaystyle {\bf A} = \int_0^\ell q(x)\,w(x) dx </math> | |||
in '''''U''''' ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir | |||
<math>\displaystyle \frac{d\phi}{x} = \frac{d\phi}{\xi}\cdot\underbrace{\displaystyle\frac{d\xi}{x}}_{\displaystyle = \frac{1}{\ell}}</math> | |||
berücksichtigen und erhalten | |||
<math>{\bf U} = \displaystyle \frac{1}{2} \cdot \displaystyle \underline{Q}^T \cdot \underline{\underline{A}}\cdot \underline{Q} - \underline{Q}^T\cdot \underline{b} </math>. | |||
In der Spaltenmatrix | |||
<math>\underline{Q} = \left( \begin{array}{l} | |||
W_{i,2}\\ | |||
\vdots\\ | |||
W_{i,I} | |||
\end{array}\right)</math> | |||
stehen nun zwischen einer und ''I-1'' Gewichtungsfaktoren ''W<sub>ij</sub> :'' die gesuchten Unbekannten. | |||
----Die Gleichgewichtsbedingungen | |||
<math>\displaystyle \frac{d{\bf U}}{dW_{ij}} \stackrel{!}{=} 0</math>, | |||
liefern uns die benötigte Anzahl von Gleichungen, z.B. für ''i=3'': | |||
<math>\begin{array}{cl} | |||
0=&{{W}_{3,3}}\cdot \left( 36+72\cdot \alpha+108\cdot {{\alpha}^{2}}+144\cdot {{\alpha}^{3}}\right) +{{W}_{3,2}}\cdot \left( 60+60\cdot \alpha+60\cdot {{\alpha}^{2}}+60\cdot {{\alpha}^{3}}\right) -30\cdot {{\alpha}^{3}}-70\cdot {{\alpha}^{2}}-50\cdot \alpha-10\\ | |||
0=&{{W}_{3,3}}\cdot \left( 36+108\cdot \alpha+216\cdot {{\alpha}^{2}}+360\cdot {{\alpha}^{3}}\right) +{{W}_{3,2}}\cdot \left( 36+72\cdot \alpha+108\cdot {{\alpha}^{2}}+144\cdot {{\alpha}^{3}}\right) -24\cdot {{\alpha}^{3}}-54\cdot {{\alpha}^{2}}-36\cdot \alpha-6 | |||
\end{array}</math>. | |||
----Hier - für ''i=3'' - ist | |||
<math>\begin{array}{ll} | |||
{{W}_{3,2}}&=\displaystyle\frac{1+8\cdot \alpha+34\cdot {{\alpha}^{2}}+94\cdot {{\alpha}^{3}}+164\cdot {{\alpha}^{4}}+148\cdot {{\alpha}^{5}}+51\cdot {{\alpha}^{6}}}{6\cdot {{\alpha}^{6}}+24\cdot {{\alpha}^{5}}+60\cdot {{\alpha}^{4}}+120\cdot {{\alpha}^{3}}+60\cdot {{\alpha}^{2}}+24\cdot \alpha+6}\\ | |||
{{W}_{3,3}}&=\displaystyle-\frac{5\cdot {{\alpha}^{2}}+20\cdot {{\alpha}^{3}}+35\cdot {{\alpha}^{4}}+30\cdot {{\alpha}^{5}}+10\cdot {{\alpha}^{6}}}{3\cdot {{\alpha}^{6}}+12\cdot {{\alpha}^{5}}+30\cdot {{\alpha}^{4}}+60\cdot {{\alpha}^{3}}+30\cdot {{\alpha}^{2}}+12\cdot \alpha+3} | |||
\end{array}</math>.{{MyCodeBlock|title=Rayleigh-Ritz Approach | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 78: | Zeile 153: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Für die verschiedenen Ansätze (Polynimial-Grade der Trial-Functions) erhaltem wir Lösungen, die die analytische Lösung aus UEBI unterschiedlich gut approximieren. Hier wählen wir als Ansätze die Polynome bis zum Grad 2, 3 und 4. | ||
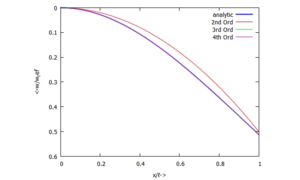
[[Datei:UEBJ-21.png|mini|Parameterstudie: Biegelinie ''w(x)'']]Und so berechnen wir die normierten Absenkungen des Balkens für die verschiedenen Ansätze: | |||
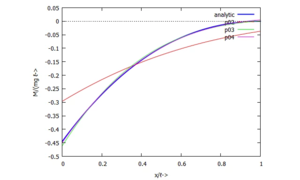
Für Moment- und Querkraftverläufe erhalten wir[[Datei:UEBJ-22.png|mini|Parameterstudie Biegemomentenverlauf ''M(x)''|alternativtext=|ohne]] | |||
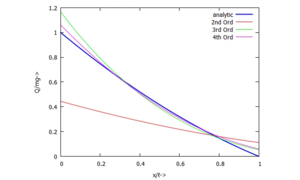
[[Datei:UEBJ-23.png|mini|Parameterstudie Querkraftverlauf ''Q(x)''|alternativtext=|ohne]]<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 95: | Zeile 174: | ||
h | h | ||
Version vom 17. April 2021, 06:20 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.
Für diese Aufgabe gibt es in UEBI eine analytische Lösung - hier schauen wir uns an, wie sich die Qualität der Näherungslösungen mit der Steigerung der Anzahl der Trial-Functions ändert.
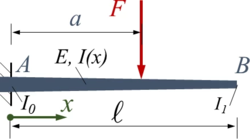
Gesucht ist die Biegeline und Schnittkraftverläufe mit dem Ansatz von Ritz und mehreren Trial-Funktionen.
Gegeben sind für den Balken:
- Länge ℓ, Breite b,
- E-Modul E, Dichte ρ und
- die Höhe h0=b und h1 jeweils in A und B; dazwischen ist die Höhe linear veränderlich.
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des einseitig fest eingespannten Balkens mit konstanten I unter einer konstanten Streckenlast q0. Hier ist die maximale Auslenkung
.
Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken.
tmp
In diesem Problem werden wir Lösungen zu verschiedenen Ansatzfunktionen miteinander vergleichen.
Es geht also nicht nur um die Berechnung einer Lösung - sondern vieler.
Header
Text
1+1
tmp
Wir arbeiten mit den System-Parametern
Für die numerische Lösung verwenden wir - wie in UEBI -
.
Declarations
Text
1+1
tmp
Gesucht ist hier ein Ansatz mit polynomialen Trial Functions. Wir probieren verschiedene Ansätze aus, die wir mit "i" kennzeichnen, also
und den gesuchten Koeffizienten Wij. Die ϕj müssen dabei alle geometrischen Randbedingungen erfüllen, also:
.
Die Funktionen müssen nicht die Randbedingungen für Schnittlasten in B erfüllen - schließlich suchen wir nach einer Näherungslösung!
Diese Funktionen ϕj zu konstruieren ist einfach: wir brauchen lediglich eine doppelte Nullstelle in . Das erreichen wir, indem wir nur Polynome ab einem Grad ≥ 2 (also jmin=2) zulassen:
.
Damit ist
.
Die freien Koeffizienten Wij sind nun die anteiligen Auslenkungen in B.
Für die Gleichgewichtsbedingungen setzten wir die Formänderungsenergie Π (aus dem Abschnitt Euler-Bernoulli-Balken)
und die Arbeitsfunktion der Gewichtskraft A
in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir
berücksichtigen und erhalten
.
In der Spaltenmatrix
stehen nun zwischen einer und I-1 Gewichtungsfaktoren Wij : die gesuchten Unbekannten.
Die Gleichgewichtsbedingungen
,
liefern uns die benötigte Anzahl von Gleichungen, z.B. für i=3:
.
Hier - für i=3 - ist
.===Rayleigh-Ritz Approach=== Text
1+1
tmp
Für die verschiedenen Ansätze (Polynimial-Grade der Trial-Functions) erhaltem wir Lösungen, die die analytische Lösung aus UEBI unterschiedlich gut approximieren. Hier wählen wir als Ansätze die Polynome bis zum Grad 2, 3 und 4.
Und so berechnen wir die normierten Absenkungen des Balkens für die verschiedenen Ansätze: Für Moment- und Querkraftverläufe erhalten wir
Post-Processing
Text
1+1
Links
- ...
Literature
- ...
h