Gelöste Aufgaben/UEBI: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 7: | Zeile 7: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Der Euler-Bernoulli-Balken ''AB'' wird durch seine Gewichtskraft belastet. Er ist in ''A'' fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe ''h''. | |||
In [[Gelöste Aufgaben/UEBF|UEBF]] haben wir eine Näherungslösung für dieses Problem berechnet. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:UEBF-01.png|alternativtext=|links|mini|200x200px|Lageplan]] | [[Datei:UEBF-01.png|alternativtext=|links|mini|200x200px|Lageplan]] | ||
Gesucht ist | Gesucht ist die analytische Lösung des Problems. | ||
</onlyinclude> | </onlyinclude> | ||
Gegeben sind für den Balken: | |||
* Länge ''ℓ'', Breite ''b,'' | |||
* E-Modul ''E'', Dichte ''ρ'' und | |||
* die Höhe ''h''<sub>0</sub>''=b'' und ''h<sub>1</sub>'' jeweils in ''A'' und ''B''; dazwischen ist die Höhe linear veränderlich. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Um zur analytischen Lösung zukommen, müssen wir berücksichtigen, dass | |||
<math>E\,I(x) \cdot \displaystyle \frac{d^2}{dx^2}w(x) = -M(x)</math>. | |||
Wir müssen also hier die Abhängigkeit der Querschnittseigenschaften von "''x''" in der Differentialbeziehung berücksichtigen. Das macht die Sache deutlich komplizierter als vorher. | |||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir haben die Differential-Beziehungen | ||
<math>\begin{array}{rcl} | |||
Q' &=&-q\\ | |||
M' &=&+Q\\ | |||
E\,I\cdot\phi' &=& -M\\ | |||
w' &=&+\phi | |||
\end{array}</math> | |||
für die Querkraft ''Q'', das Moment ''M'', die Verkippung der Querschnitte ''ϕ'' und die Auslenkung ''w''. Dabei ist die ortsabhängige Streckenlast | |||
<math>q(x) = A(x)\, \rho \, g \text{ mit } A(x) = b \cdot h(x).</math> | |||
Die Höhe des Balkens ist linear veränderlich, nämlich | |||
<math>h(x) = h_0\, (1-\xi) + h_1 \, \xi \text{ mit } \xi = \displaystyle \frac{x}{\ell}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 30: | Zeile 58: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Diese Abkürzungen führen wir ein: | ||
<math>\displaystyle m = \rho\,\frac{h_0+h_1}{2}\,b \, \ell \, g</math>, | |||
<math>h_1 = \alpha \, h_0</math>. | |||
Für die Ergebnisse setzten wir dann exemplarisch | |||
<math>\displaystyle \alpha = \frac{1}{2}</math> | |||
an - sonst werden die Ausdrücke zu umfangreich.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 41: | Zeile 81: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Beim Aufintegrieren der Differentialgleichungen stören die vielen dimensionsbehafteten Parameter. Viel einfacher werden die Gleichungen, wenn wir sie in dimensionsloser Form - mit dimensionsloser Auslenkung, Kippwinkel, Biegemoment und Querkraft anschreiben, also | ||
<math>\begin{array}{lcc} | |||
w &= W_{ref}&\cdot& \tilde{w}\\ | |||
\phi &= \Phi_{ref}&\cdot& \tilde{\phi}\\ | |||
M &= M_{ref}&\cdot& \tilde{M}\\ | |||
Q &= Q_{ref}&\cdot& \tilde{Q} | |||
\end{array}</math>. | |||
Wir wählen dazu als Referenzlösung den [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Kragbalken Streckenlast|Kragbalken mit konstantem Querschnitt unter konstanter Streckenlast]], mit der maximalen Auslenkung | |||
<math>W_{ref} = \displaystyle \frac{q_{ref} \, \ell^4}{8\,E\,I_{ref}}</math>. | |||
Als Referenz-Werte für die Streckenlast wählen wir hier die Werte unseres Balkens in ''x=ℓ/2'', demnach | |||
<math>\begin{array}{ll} | |||
q_{ref} &= A_{ref}\,\rho\,g \text{ mit } A_{ref} = b\cdot h(\displaystyle\frac{\ell}{2})\\ | |||
I_{ref} & = \displaystyle \frac{b\cdot h(\displaystyle\frac{\ell}{2})^3}{12} | |||
\end{array}</math>. | |||
Die Differentialgleichungen werden dadurch und mit der dimensionslosen Ortskoordinate | |||
<math>\xi = \displaystyle\frac{x}{\ell}</math> | |||
viel einfacher, nämlich | |||
<math>\begin{array}{rcl} | |||
\displaystyle \frac{\partial}{\partial\xi}\tilde{Q} &=& - \displaystyle\frac{4-2\xi}{3}\\ | |||
\frac{\displaystyle\partial}{\displaystyle\partial\xi} \tilde{M} &=&+\tilde{Q}\\ | |||
\frac{\displaystyle\partial}{\displaystyle\partial\xi} \tilde{\phi} &=&-\frac{\displaystyle 8}{\frac{I(\displaystyle \xi)}{\displaystyle I_{ref}}}\cdot \tilde{M} \text{ mit } \frac{\displaystyle I(\xi)}{\displaystyle I_{ref}} = \frac{\displaystyle (\alpha+1)^3}{\displaystyle 8\,((\alpha-1)\,\xi+1)^3}\\ | |||
\frac{\displaystyle \partial}{\displaystyle \partial\xi} \tilde{w} &=&+\tilde{\phi} | |||
\end{array}</math>. | |||
Damit es übersichtlicher wird, lassen wir die Tilden über den gesuchten dimensionslosen Funktionen gleich wieder weg.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Dimensionless Form of Differential Equations | {{MyCodeBlock|title=Dimensionless Form of Differential Equations | ||
|text=Text | |text=Text | ||
| Zeile 52: | Zeile 127: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Differentialbeziehungen lösen wir nun sukzessive zu | ||
<math>\displaystyle Q(\xi)=\frac{\xi^2 - 4 \xi + 3\,C_3}{3}</math>, | |||
<math>\displaystyle M(\xi)= \frac{{{\xi}^{3}}-6 {{\xi}^{2}}+9 {C_3} \xi+9 {C_2}}{9}</math>. | |||
Bis hier ist alles wie gehabt - aber jetzt steht das ortsveränderliche Flächenmoment ''I(ξ)'' im Nenner. Maxima liefert | |||
<math>\displaystyle \phi(\xi)) = \frac{6 {{\xi}^{3}}+\left( 2 {C_1}-24\right) \, {{\xi}^{2}}+\left( -54 {C_3}-8 {C_1}+96\right) \xi+54 {C_3}-27 {C_2}+8 {C_1}-96}{2 {{\xi}^{2}}-8 \xi+8}</math> | |||
und im nächsten Schritt schließlich | |||
<math>\displaystyle w(\xi) = \frac{3 {{\xi}^{3}}+\left( 2 {C_1}-6\right) \, {{\xi}^{2}}+\left( \left( 72-54 {C_3}\right) \ln{\displaystyle \left( -\frac{\xi-2}{2}\right) }-4 {C_1}+2 {C_0}\right) \xi+\left( 108 {C_3}-144\right) \ln{\displaystyle \left( -\frac{\xi-2}{2}\right) }+54 {C_3}+27 {C_2}-4 {C_0}-48}{2 \xi-4}</math>. | |||
Darin enthalten sind die unbekannten - also gesuchten - Integrationskonstanten | |||
<math>C_0, C_1, C_2, C_3</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Integration Of Differential Equation | {{MyCodeBlock|title=Integration Of Differential Equation | ||
|text=Text | |text=Text | ||
| Zeile 63: | Zeile 155: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Diese Unbekannten bestimmen wir aus den Randbedingungen, nämlich | ||
<math>\begin{array}{rcl} | |||
w(0) &=& 0\\ | |||
\phi(0) &=& 0\\ | |||
M(1) &=& 0\\ | |||
Q(1) &=& 0\\ | |||
\end{array}</math> | |||
und damit | |||
<math>\begin{array}{rcl} | |||
0&=&C_3-1\\ | |||
0&=&9 {C_3}+9 {C_2}-5\\ | |||
0&=&54 {C_3}-27 {C_2}+8 {C_1}-96\\ | |||
0&=&-54 {C_3}-27 {C_2}+4 {C_0}+48 | |||
\end{array} | |||
</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Boundary Conditions | {{MyCodeBlock|title=Boundary Conditions | ||
|text=Text | |text=Text | ||
| Zeile 74: | Zeile 186: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Zum Lösen bringen wir die Gleichungen in die Form | ||
<math>\begin{pmatrix}0 & 0 & 0 & -3\\ | |||
0 & 0 & -9 & -9\\ | |||
0 & -8 & 27 & -54\\ | |||
-4 & 0 & 27 & 54\end{pmatrix} | |||
\cdot \begin{pmatrix}{C_0}\\ | |||
{C_1}\\ | |||
{C_2}\\ | |||
{C_3}\end{pmatrix} = \begin{pmatrix}-3\\ | |||
-5\\ | |||
-96\\ | |||
48\end{pmatrix}</math>, | |||
die wir lösen zu | |||
<math>\begin{array}{lcc} | |||
C_0&=& - \displaystyle\frac{3}{2},\\ | |||
C_1&=& + \displaystyle\frac{15}{4},\\ | |||
C_2&=& - \displaystyle\frac{4}{9},\\ | |||
C_3&=& + 1 | |||
\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 85: | Zeile 220: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Ergebnisse schauen wir uns in dimensionsloser Form an, wobei wir die Standard-Lösungen für den Balken unter konstanter Streckenlast ansetzen. | ||
{{MyCodeBlock|title=Post-Processing | |||
Für | |||
<math>\begin{array}{lcl} | |||
W_{ref} &=& \displaystyle \frac{q_{ref}\cdot \ell^4}{8 EI_{ref}},\\ | |||
\Phi_{ref} &=& \displaystyle \frac{W_{ref}}{\ell},\\ | |||
M_{ref} &=& m\cdot g\cdot \ell,\\ | |||
Q_{ref} &=& m\cdot g,\\ | |||
q_{ref} &=& m\cdot g/\ell,\\ | |||
EI_{ref} &=& E\cdot \displaystyle \frac{b\cdot ((H_{0}+H_{1})/2)^3}{12} | |||
\end{array}</math> | |||
finden wir | |||
... für ''w(ξ)'': | |||
[[Datei:UEBI-31.png|mini|Auslenkung ''w(x)''|alternativtext=|ohne]]... für ''ϕ(ξ)'': | |||
[[Datei:UEBI-32.png|mini|Querschnitts-Kippung ''w'(x)''|alternativtext=|ohne]]... für ''M(ξ)'': | |||
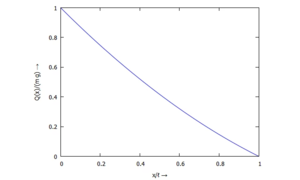
[[Datei:UEBI-33.png|mini|Momentenverlauf ''M(x)''|alternativtext=|ohne]]... für ''Q(ξ)'': | |||
[[Datei:UEBI-34.png|mini|Querkraftverlauf ''Q(x)''|alternativtext=|ohne]]<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 93: | Zeile 247: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
'''Links''' | '''Links''' | ||
Version vom 16. April 2021, 12:48 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.
In UEBF haben wir eine Näherungslösung für dieses Problem berechnet.
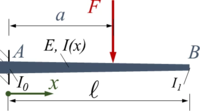
Gesucht ist die analytische Lösung des Problems.
Gegeben sind für den Balken:
- Länge ℓ, Breite b,
- E-Modul E, Dichte ρ und
- die Höhe h0=b und h1 jeweils in A und B; dazwischen ist die Höhe linear veränderlich.
Lösung mit Maxima
Um zur analytischen Lösung zukommen, müssen wir berücksichtigen, dass
.
Wir müssen also hier die Abhängigkeit der Querschnittseigenschaften von "x" in der Differentialbeziehung berücksichtigen. Das macht die Sache deutlich komplizierter als vorher.
tmp
Wir haben die Differential-Beziehungen
für die Querkraft Q, das Moment M, die Verkippung der Querschnitte ϕ und die Auslenkung w. Dabei ist die ortsabhängige Streckenlast
Die Höhe des Balkens ist linear veränderlich, nämlich
.
Header
Text
1+1
tmp
Diese Abkürzungen führen wir ein:
,
.
Für die Ergebnisse setzten wir dann exemplarisch
an - sonst werden die Ausdrücke zu umfangreich.
Declarations
Text
1+1
tmp
Beim Aufintegrieren der Differentialgleichungen stören die vielen dimensionsbehafteten Parameter. Viel einfacher werden die Gleichungen, wenn wir sie in dimensionsloser Form - mit dimensionsloser Auslenkung, Kippwinkel, Biegemoment und Querkraft anschreiben, also
.
Wir wählen dazu als Referenzlösung den Kragbalken mit konstantem Querschnitt unter konstanter Streckenlast, mit der maximalen Auslenkung
.
Als Referenz-Werte für die Streckenlast wählen wir hier die Werte unseres Balkens in x=ℓ/2, demnach
.
Die Differentialgleichungen werden dadurch und mit der dimensionslosen Ortskoordinate
viel einfacher, nämlich
.
Damit es übersichtlicher wird, lassen wir die Tilden über den gesuchten dimensionslosen Funktionen gleich wieder weg.
Dimensionless Form of Differential Equations
Text
1+1
tmp
Die Differentialbeziehungen lösen wir nun sukzessive zu
,
.
Bis hier ist alles wie gehabt - aber jetzt steht das ortsveränderliche Flächenmoment I(ξ) im Nenner. Maxima liefert
und im nächsten Schritt schließlich
.
Darin enthalten sind die unbekannten - also gesuchten - Integrationskonstanten
.
Integration Of Differential Equation
Text
1+1
tmp
Diese Unbekannten bestimmen wir aus den Randbedingungen, nämlich
und damit
.
Boundary Conditions
Text
1+1
tmp
Zum Lösen bringen wir die Gleichungen in die Form
,
die wir lösen zu
.
Solving
Text
1+1
tmp
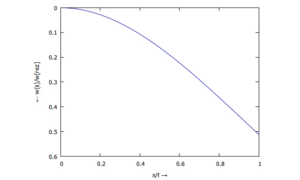
Die Ergebnisse schauen wir uns in dimensionsloser Form an, wobei wir die Standard-Lösungen für den Balken unter konstanter Streckenlast ansetzen.
Für
finden wir
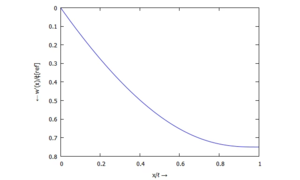
... für w(ξ):
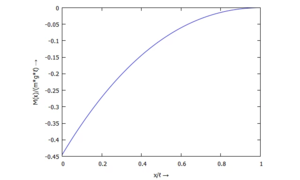
... für ϕ(ξ):
... für M(ξ):
... für Q(ξ):
===Post-Processing===
Text
1+1
Links
- ...
Literature
- ...