Gelöste Aufgaben/UEBC: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 14: | Zeile 14: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:UEBC-01.png|250px|left|mini|Lageplan]] | [[Datei:UEBC-01.png|250px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist eine Lösung für die Biegelinie ''w(x)'' mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Ansatz von Rayleigh-Ritz]] und einer Trial-Funktion. | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
= Lösung mit Maxima = | |||
Beim Verfahren von Ritz arbeiten wir mit | |||
* dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]] und | |||
* [[Sources/Lexikon/Ansatzfunktion|Ansatzfunktionen]] über die gesamte Länge des Balkens. | |||
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des beidseits gelenkig gelagerten Balkens unter einer mittigen Einzellast (vgl. [[Gelöste Aufgaben/W8Zu|W8Zu]]). Hier ist die maximale Auslenkung | |||
<math>\displaystyle w^*(\frac{\ell}{2}) = \frac{F\;\ell^3}{48\; EI} =: \hat{w}</math>. | |||
Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken. | |||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir lösen die Aufgabe mit Computer-Algebra - mit Maxima.<!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 33: | Zeile 45: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Zum Dimensionslos-Machen der Gleichungen wählen wir | ||
<math>\begin{array}{ll}W &=\displaystyle \frac{F \ell^3}{48 EI}\cdot q,\\ x&=\xi\cdot \ell,\\ a&=\alpha\cdot \ell.\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 44: | Zeile 59: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Gesucht ist hier ein Ansatz mit einer einzigen Trial Function, also | ||
<math>w(x) = W\cdot\phi(x)</math> | |||
und dem gesuchten Koeffizienten ''W''. ϕ muss dabei alle geometrischen Randbedingungen erfüllen: | |||
<math>\begin{array}{ll}w(0) &= 0,\\w'(0) &= 0,\\w(l) &= 0.\end{array}</math> | |||
Die Funktionen müssen nicht die Randbedingungen für das Moment an den Rändern ''A'' und ''B'' erfüllen! | |||
Diese Funktion zu konstruieren ist nicht ganz trivial. Wir multiplizieren dafür einzelne Terme der Form ''(x-x<sub>0</sub>)'', die die gewünschte Nullstelle für ''x=x<sub>0</sub>'' erzeugen. An der Stelle ''x=0'' benötigen wir eine doppelte Nullstelle, damit auch die Ableitung an dieser Stelle Null ist, also | |||
<math>w(\xi) = C \cdot \left( \xi-0 \right)^2 \cdot \left(\xi-1\right) \text {mit }\xi = \displaystyle\frac{x}{\ell}</math>. | |||
Den freien Koeffizienten ''C'' wählen wir so, dass wir ihn anschaulich "denken" können - wir wählen die gesuchte Auslenkung an der Kraft-Einleitungsstelle ''x=a'' aus [[Gelöste Aufgaben/W8Zu|W8Zu]], also | |||
<math>\displaystyle w(a) = q\cdot \hat{w} \;\;\text{ mit der Referenz-Lösung }\;\; \hat{w} = \frac{F\;\ell^3}{48\; EI} </math>. | |||
Mit der neuen, dimensionslosen Koordinate ''q'' ist | |||
<math>\displaystyle C = \frac{q\cdot \hat{w}}{\alpha^3-\alpha}</math>, | |||
und damit | |||
<math>\displaystyle w(x) = \underbrace{\frac{F \ell^3}{48 EI }\cdot q}_{\displaystyle =W} \cdot \underbrace{\frac{{{\xi}^{3}}-{{\xi}^{2}}}{{{\alpha}^{3}}-{{\alpha}^{2}}}}_{\displaystyle =\phi(\xi)}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
| Zeile 55: | Zeile 96: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Für die Gleichgewichtsbedingungen setzten wir ''Π'' und ''A'' in ''U'' ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir | ||
<math>\displaystyle \frac{d\phi}{x} = \frac{d\phi}{\xi}\cdot\underbrace{\displaystyle\frac{d\xi}{x}}_{\displaystyle = \frac{1}{\ell}}</math> | |||
berücksichtigen und erhalten | |||
<math>U = \displaystyle \frac{1}{2} \cdot \displaystyle \underline{Q}^T \cdot \underline{\underline{A}}\cdot \underline{Q} - \underline{Q}^T\cdot \underline{b} </math>. | |||
Weil wir in | |||
<math>\underline{Q} = \left(q\right)</math> | |||
nur eine Unbekannte ''q'' haben, können wir es uns hier etwas einfacher machen, ''U'' lautet: | |||
<math>\displaystyle U=\frac{\left( \left( -24\cdot {{\alpha}^{6}}+48\cdot {{\alpha}^{5}}-24\cdot {{\alpha}^{4}}\right) \cdot {{\ell}^{3}}\cdot q+{{\ell}^{3}}\cdot {{q}^{2}}\right) \cdot {{F}^{2}}}{\left( 1152\cdot {{\alpha}^{6}}-2304\cdot {{\alpha}^{5}}+1152\cdot {{\alpha}^{4}}\right) \cdot \mathit{EI}}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Potential Energy | {{MyCodeBlock|title=Potential Energy | ||
|text=Text | |text=Text | ||
| Zeile 66: | Zeile 122: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Diese Gleichung erfüllt die Gleichgewichtsbedingungen | ||
<math>\displaystyle \frac{dU}{dW} \stackrel{!}{=} 0</math>, | |||
wenn | |||
<math>\displaystyle \frac{\left( -12\cdot {{\alpha}^{4}}+24\cdot {{\alpha}^{5}}-12\cdot {{\alpha}^{6}}+q\right) \cdot F}{12\cdot {{\alpha}^{6}}-24\cdot {{\alpha}^{5}}+12\cdot {{\alpha}^{4}}}=0</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 77: | Zeile 141: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Diese Gleichgewichtsbedingung ist erfüllt , wenn | ||
<math>q=12\cdot {{\alpha}^{6}}-24\cdot {{\alpha}^{5}}+12\cdot {{\alpha}^{4}}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 87: | Zeile 155: | ||
==tmp== | ==tmp== | ||
[[Datei:UEBC-11.png|mini|Auslenkung ''w(x)'']]Wir schauen uns zunächst die Absenkung des Kraftangriffspunktes ''w(a)'' für verschiedene Werte von ''a (α)'' an: | |||
<!--------------------------------------------------------------------------------> | Die maximale Auslenkung des Kraftangriffspunktes ist hier bei ''α''=2/3 erreicht. Das ist nicht identisch mit der größten Absenkung der Querschnitte im Gebiet![[Datei:UEBC-12.png|mini|Parameter-Studie für ''α''|alternativtext=|links]]Dafür schauen wir uns den Verlauf der approximierten Biegelinie an - und zwar für verschiedene Werte von ''α'': | ||
Sie sehen, dass für ''α=6/10'' die Auslenkung dieses Systems nur ein Viertel der maximalen Auslenkung eines beidseitig gelenkig gelagerten Balkens beträgt - jedenfalls in unserer Approximation mit einer Trial-Funktion. | |||
Aufgabe [[Gelöste Aufgaben/UEBD|UEBD]] zeigt, wie wir zu einer besseren Approximation kommen. | |||
{{MyTip|title=Schnittmomenten-Verlauf|text=Probieren Sie aus, wie gut der Ritz-Ansatz den Verlauf des Schnittmoments approximiert!}}<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 104: | Zeile 178: | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | * ... | ||
| Zeile 110: | Zeile 184: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Version vom 14. April 2021, 08:33 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch eine vertikale Einzelkraft F belastet. Er ist in A fest eingespannt, in B gelenkig gelagert.
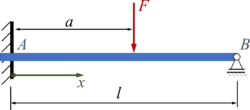
Gesucht ist eine Lösung für die Biegelinie w(x) mit dem Ansatz von Rayleigh-Ritz und einer Trial-Funktion.
Lösung mit Maxima
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des beidseits gelenkig gelagerten Balkens unter einer mittigen Einzellast (vgl. W8Zu). Hier ist die maximale Auslenkung
.
Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken.
tmp
Wir lösen die Aufgabe mit Computer-Algebra - mit Maxima.
Header
Text
1+1
tmp
Zum Dimensionslos-Machen der Gleichungen wählen wir
.
Declarations
Text
1+1
tmp
Gesucht ist hier ein Ansatz mit einer einzigen Trial Function, also
und dem gesuchten Koeffizienten W. ϕ muss dabei alle geometrischen Randbedingungen erfüllen:
Die Funktionen müssen nicht die Randbedingungen für das Moment an den Rändern A und B erfüllen!
Diese Funktion zu konstruieren ist nicht ganz trivial. Wir multiplizieren dafür einzelne Terme der Form (x-x0), die die gewünschte Nullstelle für x=x0 erzeugen. An der Stelle x=0 benötigen wir eine doppelte Nullstelle, damit auch die Ableitung an dieser Stelle Null ist, also
.
Den freien Koeffizienten C wählen wir so, dass wir ihn anschaulich "denken" können - wir wählen die gesuchte Auslenkung an der Kraft-Einleitungsstelle x=a aus W8Zu, also
.
Mit der neuen, dimensionslosen Koordinate q ist
,
und damit
.
Formfunctions
Text
1+1
tmp
Für die Gleichgewichtsbedingungen setzten wir Π und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir
berücksichtigen und erhalten
.
Weil wir in
nur eine Unbekannte q haben, können wir es uns hier etwas einfacher machen, U lautet:
.
Potential Energy
Text
1+1
tmp
Diese Gleichung erfüllt die Gleichgewichtsbedingungen
,
wenn
.
Equilibrium Conditions
Text
1+1
tmp
Diese Gleichgewichtsbedingung ist erfüllt , wenn
.
Solving
Text
1+1
tmp
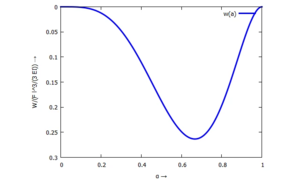
Wir schauen uns zunächst die Absenkung des Kraftangriffspunktes w(a) für verschiedene Werte von a (α) an: Die maximale Auslenkung des Kraftangriffspunktes ist hier bei α=2/3 erreicht. Das ist nicht identisch mit der größten Absenkung der Querschnitte im Gebiet!
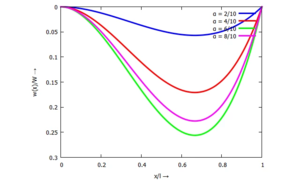
Dafür schauen wir uns den Verlauf der approximierten Biegelinie an - und zwar für verschiedene Werte von α:
Sie sehen, dass für α=6/10 die Auslenkung dieses Systems nur ein Viertel der maximalen Auslenkung eines beidseitig gelenkig gelagerten Balkens beträgt - jedenfalls in unserer Approximation mit einer Trial-Funktion.
Aufgabe UEBD zeigt, wie wir zu einer besseren Approximation kommen.
| ✔ Schnittmomenten-Verlauf: |
| Probieren Sie aus, wie gut der Ritz-Ansatz den Verlauf des Schnittmoments approximiert! |
Post-Processing
Text
1+1
Links
- ...
Literature
- ...