Gelöste Aufgaben/Tzul: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Caption 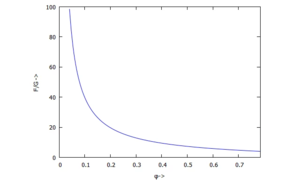
Erforderliche Kraft F/G
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 43: | Zeile 43: | ||
<math>\displaystyle F=\frac{4\cdot \sqrt{16\cdot {{\ell}^{2}}-{{h}^{2}}}\cdot G}{h}</math>[[Datei:Tzul-11.png|mini|Erforderliche Kraft ''F/G'']]Auftragen von F über den Scherenwinkel liefert | <math>\displaystyle F=\frac{4\cdot \sqrt{16\cdot {{\ell}^{2}}-{{h}^{2}}}\cdot G}{h}</math>[[Datei:Tzul-11.png|mini|Erforderliche Kraft ''F/G'']]Auftragen von F über den Scherenwinkel liefert | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Implementierung in Maxima | {{MyCodeBlock|title=Implementierung in Maxima | ||
| Zeile 71: | Zeile 68: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
Version vom 9. April 2021, 13:16 Uhr
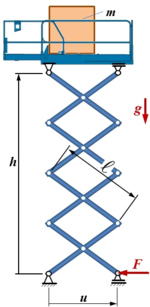
Aufgabenstellung
Hier spielt das Prinzip der virtuellen Verrückungen seine Stärke voll aus:

Auf der skizzierten Scherenbühne mit Stablänge ℓ steht eine Masse m.
Berechnen Sie die Kraft F als Funktion der Höhe h.
Hinweis: diese Aufgabe lässt sich gut mit dem Prinzip der virtuellen Arbeit unter
Verwendung der Koordinate u lösen.
Gegeben: ℓ, m, g
Lösung mit Maxima
Die Kinematik, also den Zusammenhang zwischen u und h erhalten wir aus dem Satz von Pythagoras:
Daraus kommt:
und,
.
Mit dem Prinzip der virtuellen Verrückungen lautet die Gleichgewichtsbedingung:
Die erforderliche Kraft F ist:

Auftragen von F über den Scherenwinkel liefert
Implementierung in Maxima
Die Formeln lassen sich leicht in Maxima schrieiben:
/* declare variational variables */
declare("δW", alphabetic);
declare("δu", alphabetic);
declare("δh", alphabetic);
/* Principle of virtual Work */
δW : -F*δu - G*δh;
/* kinematics */
kin: solve(u^2+(h/4)^2=l^2,u)[2];
varia: [δu = diff(rhs(kin),h)*δh];
/* solve */
sol: solve(subst(varia,δW)=0,F);
/* plot results */
plot2d(4/tan(phi),[phi,0,%pi/4], [x,0,%pi/4], [y,0,100],
[ylabel, "F/G ->"], [xlabel, "φ->"]);
Links
- ...
Literature
- ...