Gelöste Aufgaben/T401

Aufgabenstellung

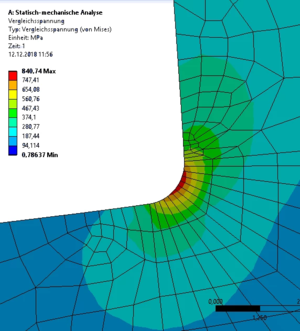
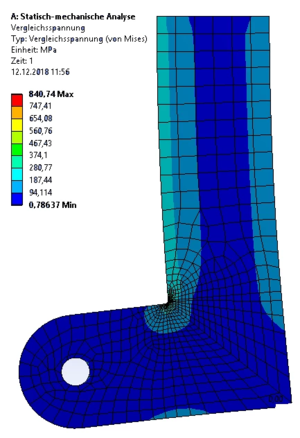
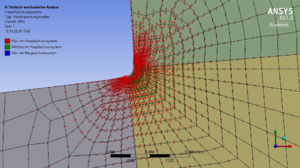
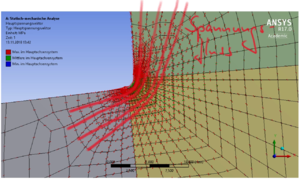
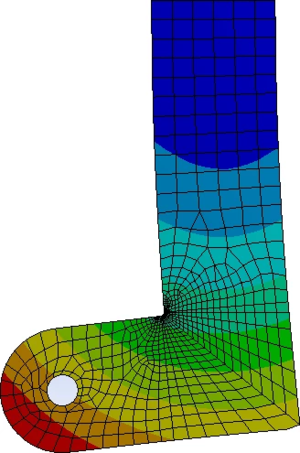
Wie ein FE-Programm die Hauptspannungen aus dem Verschiebungsfeld berechnet und wie wir das Feld der Hauptspannungen im Gebiet zur Interpretation des "Spannungsflusses" nutzen, beschreibt dieses gelöste Problem.

Lageplan

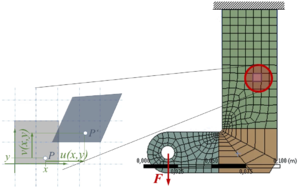
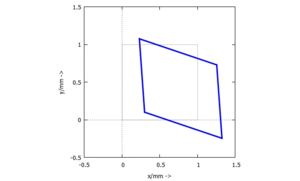
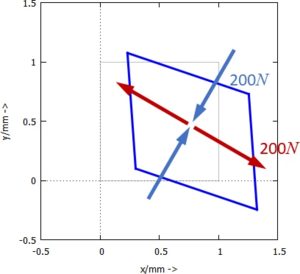
Bei der Analyse eines ebenen Bauteils wird der Verschiebungszustand eines Finiten Elementes durch

${\begin{array}{llll}u(x,y)=&u_{0}&+e_{x,x}\cdot x&+e_{x,y}\cdot y&{\text{ und }}\\v(x,y)=&v_{0}&+e_{y,x}\cdot x&+e_{y,y}\cdot y&\end{array}}$

erfasst.

Gesucht sind die Hauptspannungen und Hauptspannungs-Richtungen im Finiten Element.

Dabei werden die Koeffizienten des Verschiebungsfeldes mit

$\displaystyle {{e}_{x,x}}={\frac {1}{800}},{{e}_{y,y}}=-{\frac {1}{800}},{{e}_{y,x}}={\frac {{e}_{x,y}}{4}},{{e}_{x,y}}=-{\frac {\sqrt {3}}{500}}$

angegeben. Die Material-Parameter sind

$\displaystyle \nu ={\frac {1}{4}},E=100000\cdot {\frac {\text{N}}{{\text{mm}}^{2}}}$,

das Finite Elemente hat eine Kantenlänge von jeweils 1 mm.

tmp

Hauptspannungsrichtungen sind Schnittnormalen im Element, bei denen die Schubspannungen auf den Schnittflächen verschwinden.

Alle Vergleichsspannungs-Hypothesen gehen von den Spannungen in den Hauptspannungsrchtungen aus.

Title

Text

1+1

---

Links

• ...

Literature

• ...

Vergleichsspannung im kritischen Bereich

Spannungen

Verformtes Element

Hauptspannungen

Spannungsfluss-Analogie

Legende

Verschiebungen der Knoten

Lageplan

Hauptspannungen