Gelöste Aufgaben/T313: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
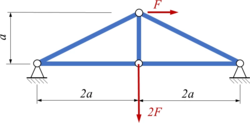
Lageplan
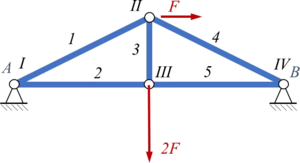
Bezeichnung von Stäben und Knoten 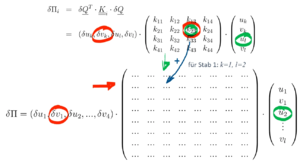
Einarbeiten der Element-Steifigkeitsmatrix 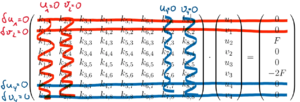
Randbedingungen einarbeiten 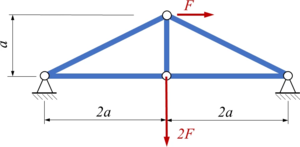
Lageplan
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:A*x=b]] | |||
[[Category:Analytische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Prinzip der virtuellen Verrückungen]] | |||
[[Category:Formänderungsenergie]] | |||
[[Category:Dehnstab]] | |||
[[Category:Maxima]] | |||
[[Category:Stabwerk]] | |||
==Aufgabenstellung== | |||
Stäbe waren früher das zentrale Bauteil in Leichtbau-Konstruktionen. In dieser Aufgabe geht es um die Komposition der Gesamt-Steifigkeitsmatrix für ein Stabwerk. | |||
Das Stabwerk besteht aus 5 Stäben gleicher Dehnsteifigkeit EA und wird durch die Kräfte ''F, 2F'' belastet. | |||
<onlyinclude> | |||
[[Datei:T313-01.png|250px|left|mini|Lageplan]] | |||
Gesucht sind Stabkräfte und Verschiebung der Knotenpunkte des Systems mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der vertuellen Verrückungen]]. | |||
</onlyinclude> | |||
== Lösung mit Maxima == | |||
Dazu verwenden wir die Element-Steifigkeitsmatrix aus den Ergebnissen von Aufgabe [[Gelöste Aufgaben/T312|T312]]. | |||
In der Gleichgewichtsbedinung beim Prinzip der virtuellen Verrückungen | |||
teilen wir | |||
in die virtuelle Formänderungsenergie δΠi je Stab auf. | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Title | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Element Stiffness Matrix | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Compose total Stiffness Matrix | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Boundary Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<table class="wikitable" style="background-color:white; float: left; margin-right:14px; | |||
"> | |||
<tr><th></th><th></th></tr> | |||
<tr><td></td><td></td></tr> | |||
</table> | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
[[Datei:T313-11.png|mini|Bezeichnung von Stäben und Knoten]] | [[Datei:T313-11.png|mini|Bezeichnung von Stäben und Knoten]] | ||
Version vom 5. April 2021, 15:09 Uhr
Aufgabenstellung
Stäbe waren früher das zentrale Bauteil in Leichtbau-Konstruktionen. In dieser Aufgabe geht es um die Komposition der Gesamt-Steifigkeitsmatrix für ein Stabwerk. Das Stabwerk besteht aus 5 Stäben gleicher Dehnsteifigkeit EA und wird durch die Kräfte F, 2F belastet.

Gesucht sind Stabkräfte und Verschiebung der Knotenpunkte des Systems mit dem Prinzip der vertuellen Verrückungen.
Lösung mit Maxima
Dazu verwenden wir die Element-Steifigkeitsmatrix aus den Ergebnissen von Aufgabe T312.
In der Gleichgewichtsbedinung beim Prinzip der virtuellen Verrückungen
teilen wir
in die virtuelle Formänderungsenergie δΠi je Stab auf.
tmp
Header
Text
1+1
tmp
Title
Text
1+1
tmp
Element Stiffness Matrix
Text
1+1
tmp
Compose total Stiffness Matrix
Text
1+1
tmp
Boundary Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
Links
- ...
Literature
- ...



