Gelöste Aufgaben/T312: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 15: | Zeile 15: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Die relevanten Größen wie ''die Stablänge ℓ<sub>i</sub>'', die Stablängung ''Δℓ<sub>i</sub>'' und die Stabkraft ''S''<sub>i</sub> sind im Stabsystem definiert, wir brauchen aber die Größen in einem einheitlichen ''x,y'' - Referenzsystem. | Die relevanten Größen wie ''die Stablänge ℓ<sub>i</sub>'', die Stablängung ''Δℓ<sub>i</sub>'' und die Stabkraft ''S''<sub>i</sub> sind im Stabsystem definiert, wir brauchen aber die Größen in einem einheitlichen ''x,y'' - Referenzsystem. | ||
| Zeile 23: | Zeile 20: | ||
Damit wir also nicht bei jeder Aufgabe wieder von vorn anfangen, die ''Δℓ<sub>i</sub>'' als Funktion der Auslenkungen ''u<sub>j</sub>, v<sub>j</sub>'' der Knoten ''K,L'' im ''x,y'' - System herzuleiten, machen wir das ein Mal allgemein. | Damit wir also nicht bei jeder Aufgabe wieder von vorn anfangen, die ''Δℓ<sub>i</sub>'' als Funktion der Auslenkungen ''u<sub>j</sub>, v<sub>j</sub>'' der Knoten ''K,L'' im ''x,y'' - System herzuleiten, machen wir das ein Mal allgemein. | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Dazu vergleichen wir den Stab in seiner verformten Konfiguration mit seiner Referenzkonfiguration - und schreiben die Terme der virtuellen Formänderungsenergie an. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-10-31 */ | |||
/* ref: TM-2 */ | |||
/* description: virt. Formänderungsarbeit eines Stabes */ | |||
/* in einem Stabwerk */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text= | |text= | ||
Hier stehen nur die Deklarationen für spezielle Symbole zur Verwendung mit Maxima. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/* special symbols to be declared */ | |||
declare("δΠ", alphabetic); | |||
declare("δl", alphabetic); | |||
declare("Δl", alphabetic); | |||
declare("Δx", alphabetic); | |||
declare("Δy", alphabetic); | |||
declare("δu", alphabetic); | |||
declare("δv", alphabetic); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Kinematics | |||
|text= | |||
[[Datei:T312-11.png|mini|Koordinaten]]Der Stab ''i'' hat die Knoten ''K'' und ''L'', die im unverformten Stabwerk die Koordinaten | [[Datei:T312-11.png|mini|Koordinaten]]Der Stab ''i'' hat die Knoten ''K'' und ''L'', die im unverformten Stabwerk die Koordinaten | ||
<math>\begin{array}{ll}P_K: [x_k, y_k]\\P_L: [x_l, y_l] \end{array}</math> | ::<math>\begin{array}{ll}P_K: [x_k, y_k]\\P_L: [x_l, y_l] \end{array}</math> | ||
haben. | haben. | ||
| Zeile 56: | Zeile 68: | ||
Im verformten System sind | Im verformten System sind | ||
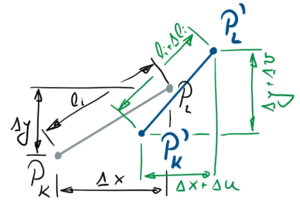
<math>\begin{array}{llc}P'_K: [x_k+u_k,& y_k+v_k],\\P'_L: [x_l+u_l,& y_l+v_l] \end{array}</math>''.''[[Datei:T312-12.png|mini|Kinematische Verträglichkeit]]Mit dem Satz von Pythagoras stellen wir nun den Zusammenhang her zwischen der Stablänge in der Ausgangskonfiguration und der verformten Konfiguration des Stabes: | ::<math>\begin{array}{llc}P'_K: [x_k+u_k,& y_k+v_k],\\P'_L: [x_l+u_l,& y_l+v_l] \end{array}</math>''.''[[Datei:T312-12.png|mini|Kinematische Verträglichkeit]]Mit dem Satz von Pythagoras stellen wir nun den Zusammenhang her zwischen der Stablänge in der Ausgangskonfiguration und der verformten Konfiguration des Stabes: | ||
<math>\begin{array}{rcc}{{ \left( {{y}_{l}}-{{y}_{k}}\right) }^{2}}+{{\left( {{x}_{l}}-{{x}_{k}}\right) }^{2}}&=&{{\ell}_{i}^{2}}\\{{\left( (v_l-v_k) + (y_l-y_k)\right)^2 + \left( (u_l-u_k) + (x_l-x_k) \right) }^{2}}&=&{{\left( {{ \ell}_{i}}+{{\mathit{\Delta \ell}}_{i}}\right) }^{2}}\end{array}</math> | ::<math>\begin{array}{rcc}{{ \left( {{y}_{l}}-{{y}_{k}}\right) }^{2}}+{{\left( {{x}_{l}}-{{x}_{k}}\right) }^{2}}&=&{{\ell}_{i}^{2}}\\{{\left( (v_l-v_k) + (y_l-y_k)\right)^2 + \left( (u_l-u_k) + (x_l-x_k) \right) }^{2}}&=&{{\left( {{ \ell}_{i}}+{{\mathit{\Delta \ell}}_{i}}\right) }^{2}}\end{array}</math> | ||
Die zweite Zeile stellt den nichtlinearen Zusammenhang zwischen den Koordinaten der Knoten-Verschiebungen ''u<sub>j</sub>'',''v<sub>j</sub>'' und der Stablängung ''Δℓ<sub>i</sub>'' her. | Die zweite Zeile stellt den nichtlinearen Zusammenhang zwischen den Koordinaten der Knoten-Verschiebungen ''u<sub>j</sub>'',''v<sub>j</sub>'' und der Stablängung ''Δℓ<sub>i</sub>'' her. | ||
| Zeile 66: | Zeile 78: | ||
Wir linearisieren deshalb den Ausdruck oben und erhalten | Wir linearisieren deshalb den Ausdruck oben und erhalten | ||
<math>\Delta\,\ell_i = \displaystyle \frac{(x_l-x_k)\cdot (u_l-u_k)+(y_l-y_k)\cdot (v_l-v_k)}{\ell_i}</math> | ::<math>\Delta\,\ell_i = \displaystyle \frac{(x_l-x_k)\cdot (u_l-u_k)+(y_l-y_k)\cdot (v_l-v_k)}{\ell_i}</math> | ||
den wir den Abkürzungen | den wir den Abkürzungen | ||
<math>\begin{array}{ll}{{x}_{l}}&=\mathit{\Delta x}+{{x}_{k}}\\ {{y}_{l}}&=\mathit{\Delta y}+{{y}_{k}}\\ \mathit{\Delta x}&={{\ell}_{i}}\cdot {{\xi}_{x}}\ \mathit{\Delta y}&={{\ell}_{i}}\cdot {{\xi}_{y}}\\ {{\mathit{EA}}_{i}}&={{k}_{i}}\cdot {{\ell}_{i}}\end{array}</math> | ::<math>\begin{array}{ll}{{x}_{l}}&=\mathit{\Delta x}+{{x}_{k}}\\ {{y}_{l}}&=\mathit{\Delta y}+{{y}_{k}}\\ \mathit{\Delta x}&={{\ell}_{i}}\cdot {{\xi}_{x}}\ \mathit{\Delta y}&={{\ell}_{i}}\cdot {{\xi}_{y}}\\ {{\mathit{EA}}_{i}}&={{k}_{i}}\cdot {{\ell}_{i}}\end{array}</math> | ||
schrieben als | schrieben als | ||
<math>{{\mathit{\Delta \ell}}_{i}}=\left( {{v}_{l}}-{{v}_{k}}\right) \cdot {{\xi}_{y}}+\left( {{u}_{l}}-{{u}_{k}}\right) \cdot {{\xi}_{x}}</math>.< | ::<math>{{\mathit{\Delta \ell}}_{i}}=\left( {{v}_{l}}-{{v}_{k}}\right) \cdot {{\xi}_{y}}+\left( {{u}_{l}}-{{u}_{k}}\right) \cdot {{\xi}_{x}}</math>. | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* coordinates */ | |||
q : [[ u[k], v[k], u[l], v[l],Δl[i]], | |||
[δu[k],δv[k],δu[l],δv[l],δl[i]]]; | |||
/* refernce Points */ | |||
points: [P[k]=matrix([x[k]],[y[k]]), | |||
P[l]=matrix([x[l]],[y[l]]), | |||
p[k]=matrix([x[k]+u[k]],[y[k]+v[k]]), | |||
p[l]=matrix([x[l]+u[l]],[y[l]+v[l]])]; | |||
length: [subst(points,P[l])-subst(points,P[k]), | |||
subst(points,p[l])-subst(points,p[k])]; | |||
pythagoras: [transpose(length[1]).length[1] = l[i]^2, | |||
1+ | transpose(length[2]).length[2] = (l[i]+Δl[i])^2]; | ||
kinematics: lhs(pythagoras[2])-lhs(pythagoras[1]) = | |||
rhs(pythagoras[2])-rhs(pythagoras[1]); | |||
sol : solve(taylor(kinematics, | |||
q[1],0,1),Δl[i])[1]; | |||
/* abbreviations */ | |||
simple : [x[l]=x[k]+Δx, y[l]=y[k]+Δy, | |||
Δx = xi[x]*l[i], Δy = xi[y]*l[i], EA[i]=k[i]*l[i]]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Virtual Strain Energy | |||
|text= | |||
Mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] schreiben wir die Gleichgewichtsbedingungen als | Mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] schreiben wir die Gleichgewichtsbedingungen als | ||
<math>\delta W = \delta W^a - \delta \Pi</math> | ::<math>\delta W = \delta W^a - \delta \Pi</math> | ||
mit der virtuellen Formänderungsenergie ''δΠ'' aller Stäbe des Systems, also | mit der virtuellen Formänderungsenergie ''δΠ'' aller Stäbe des Systems, also | ||
<math>\delta\Pi = \displaystyle\sum_i \delta \Pi_i</math> | ::<math>\delta\Pi = \displaystyle\sum_i \delta \Pi_i</math> | ||
Für einen einzelnen Stab schrieben wir jetzt | Für einen einzelnen Stab schrieben wir jetzt | ||
<math>\begin{array}{ll}\delta\Pi&=\displaystyle A_i \int_\ell \sigma \cdot \delta\epsilon \; d\tilde{x}\\&=k_i \cdot \Delta \ell_i\cdot \delta \ell_i\end{array}</math> | ::<math>\begin{array}{ll}\delta\Pi&=\displaystyle A_i \int_\ell \sigma \cdot \delta\epsilon \; d\tilde{x}\\&=k_i \cdot \Delta \ell_i\cdot \delta \ell_i\end{array}</math> | ||
mit | mit | ||
<math>\displaystyle k_i = \frac{E\,A}{\ell_i}</math>. | ::<math>\displaystyle k_i = \frac{E\,A}{\ell_i}</math>. | ||
Mit den Ergebnissen von oben setzen wir also | Mit den Ergebnissen von oben setzen wir also | ||
in ''δΠ<sub>i</sub>'' ein. | in ''δΠ<sub>i</sub>'' ein. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* Einsetzen in das PvV */ | ||
sol : [sol, subst( | |||
makelist(q[1][i]=q[2][i],i,1,5), sol)]; | |||
VSE: δΠ[i] = EA[i]/l[i]*Δl[i]*δl[i]; | |||
VSE : expand(subst(sol,VSE)); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title= | |||
Die Terme schreiben wir noch etwas um, so dass man die Struktur hinter der virtuellen Formänderungsenergie erkennt - und erhalten: | Die Terme schreiben wir noch etwas um, so dass man die Struktur hinter der virtuellen Formänderungsenergie erkennt - und erhalten: | ||
<math>\delta\Pi_i={{k}_{i}}\cdot [{{\mathit{\delta\,u}}_{k}},{{\mathit{\delta\,v}}_{k}},{{\mathit{\delta\,u}}_{l}},{{\mathit{\delta\,v}}_{l}}]\cdot \underbrace{\begin{pmatrix}{{\xi}_{x}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{x}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}}\\ {{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}}\\ -{{\xi}_{x}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{x}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}}\\ -{{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}}\end{pmatrix}}_{ \displaystyle =:\underline{\underline{K}}_E }\cdot \begin{pmatrix}{{u}_{k}}\\ {{v}_{k}}\\ {{u}_{l}}\\ {{v}_{l}}\end{pmatrix}</math> | ::<math>\delta\Pi_i={{k}_{i}}\cdot [{{\mathit{\delta\,u}}_{k}},{{\mathit{\delta\,v}}_{k}},{{\mathit{\delta\,u}}_{l}},{{\mathit{\delta\,v}}_{l}}]\cdot \underbrace{\begin{pmatrix}{{\xi}_{x}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{x}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}}\\ {{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}}\\ -{{\xi}_{x}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{x}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}}\\ -{{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}}\end{pmatrix}}_{ \displaystyle =:\underline{\underline{K}}_E }\cdot \begin{pmatrix}{{u}_{k}}\\ {{v}_{k}}\\ {{u}_{l}}\\ {{v}_{l}}\end{pmatrix}</math>. | ||
|text=Text | |text=Text | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* Element-Steifigkeitsmatrix K definieren */ | ||
K : makelist(makelist(coeff( | |||
coeff(subst(VSE, δΠ[i]),q[2][m]),q[1][n]), | |||
m,1,4),n,1,4); | |||
print('δΠ[i],"=",k[i],"*",rest(q[2],-1),"*", | |||
funmake('matrix,ratsimp(subst(simple,K/k[i]))),"*", | |||
transpose(rest(q[1],-1))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | |||
<!--------------------------------------------------------------------------------> | |||
==Post-Processing== | |||
Stabwerkskräfte und deren Knoten-Verschiebungen können wir nun mit geringem Aufwand bearbeiten: | Stabwerkskräfte und deren Knoten-Verschiebungen können wir nun mit geringem Aufwand bearbeiten: | ||
| Zeile 136: | Zeile 177: | ||
Das wäre zwar anschaulich richtig - aber unpraktisch. So würden wir große Ausdrücke erhalten für ''δΠ''. Einfacher und für die Behandlung mit dem Computer praktischer ist folgendes Vorgehen: | Das wäre zwar anschaulich richtig - aber unpraktisch. So würden wir große Ausdrücke erhalten für ''δΠ''. Einfacher und für die Behandlung mit dem Computer praktischer ist folgendes Vorgehen: | ||
Ausgangspunkt ist | Ausgangspunkt ist die Element-Steifigkeitsmatrix | ||
::<math>{\underline{\underline{K}}_{E}}</math>. | |||
<math>{\underline{\underline{K}}_{E}}</math> | |||
Wir erzeugen uns eine Steifigkeitsmatrix für die Verschiebungen aller Knoten des Stabwerks und sortieren die Elemente der Element-Steifigkeitsmatrix sukzessive und additiv in diese ein. | Wir erzeugen uns eine Steifigkeitsmatrix für die Verschiebungen aller Knoten des Stabwerks und sortieren die Elemente der Element-Steifigkeitsmatrix sukzessive und additiv in diese ein. | ||
Wie das geht, zeigt [[Gelöste Aufgaben/T313|T313]]. | Wie das geht, zeigt [[Gelöste Aufgaben/T313|T313]]. | ||
<hr /> | <hr /> | ||
Version vom 4. April 2021, 17:57 Uhr
Aufgabenstellung
Bei Arbeiten mit elastischen Stäben stoßen wir immer wieder auf die gleiche Aufgabe: das Aufstellen der virtuellen Formänderungsenergie eines Stabes, den wir in ein System einbauen müssen.
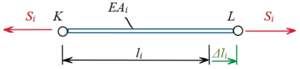
Gesucht ist die allgemeine Formulierung für die virtuelle Formänderungsenergie eines Stabes in einem Stabwerk.
Lösung mit Maxima
Die relevanten Größen wie die Stablänge ℓi, die Stablängung Δℓi und die Stabkraft Si sind im Stabsystem definiert, wir brauchen aber die Größen in einem einheitlichen x,y - Referenzsystem.
Damit wir also nicht bei jeder Aufgabe wieder von vorn anfangen, die Δℓi als Funktion der Auslenkungen uj, vj der Knoten K,L im x,y - System herzuleiten, machen wir das ein Mal allgemein.
Header
Dazu vergleichen wir den Stab in seiner verformten Konfiguration mit seiner Referenzkonfiguration - und schreiben die Terme der virtuellen Formänderungsenergie an.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-10-31 */
/* ref: TM-2 */
/* description: virt. Formänderungsarbeit eines Stabes */
/* in einem Stabwerk */
/*******************************************************/
Declarations
Hier stehen nur die Deklarationen für spezielle Symbole zur Verwendung mit Maxima.
/* special symbols to be declared */
declare("δΠ", alphabetic);
declare("δl", alphabetic);
declare("Δl", alphabetic);
declare("Δx", alphabetic);
declare("Δy", alphabetic);
declare("δu", alphabetic);
declare("δv", alphabetic);
Kinematics
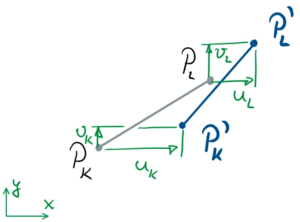
Der Stab i hat die Knoten K und L, die im unverformten Stabwerk die Koordinaten
haben.
Im verformten System sind
Die zweite Zeile stellt den nichtlinearen Zusammenhang zwischen den Koordinaten der Knoten-Verschiebungen uj,vj und der Stablängung Δℓi her.
Den nichtlinearen Zusammenhang brauchen wir praktisch nie, weil wir meist von kleinen Verformungen des Systems ausgehen - und damit auch kleinen Stablängungen ausgehen.
Wir linearisieren deshalb den Ausdruck oben und erhalten
den wir den Abkürzungen
schrieben als
- .
/* coordinates */
q : [[ u[k], v[k], u[l], v[l],Δl[i]],
[δu[k],δv[k],δu[l],δv[l],δl[i]]];
/* refernce Points */
points: [P[k]=matrix([x[k]],[y[k]]),
P[l]=matrix([x[l]],[y[l]]),
p[k]=matrix([x[k]+u[k]],[y[k]+v[k]]),
p[l]=matrix([x[l]+u[l]],[y[l]+v[l]])];
length: [subst(points,P[l])-subst(points,P[k]),
subst(points,p[l])-subst(points,p[k])];
pythagoras: [transpose(length[1]).length[1] = l[i]^2,
transpose(length[2]).length[2] = (l[i]+Δl[i])^2];
kinematics: lhs(pythagoras[2])-lhs(pythagoras[1]) =
rhs(pythagoras[2])-rhs(pythagoras[1]);
sol : solve(taylor(kinematics,
q[1],0,1),Δl[i])[1];
/* abbreviations */
simple : [x[l]=x[k]+Δx, y[l]=y[k]+Δy,
Δx = xi[x]*l[i], Δy = xi[y]*l[i], EA[i]=k[i]*l[i]];
Virtual Strain Energy
Mit dem Prinzip der virtuellen Verrückungen schreiben wir die Gleichgewichtsbedingungen als
mit der virtuellen Formänderungsenergie δΠ aller Stäbe des Systems, also
Für einen einzelnen Stab schrieben wir jetzt
mit
- .
Mit den Ergebnissen von oben setzen wir also
in δΠi ein.
/* Einsetzen in das PvV */
sol : [sol, subst(
makelist(q[1][i]=q[2][i],i,1,5), sol)];
VSE: δΠ[i] = EA[i]/l[i]*Δl[i]*δl[i];
VSE : expand(subst(sol,VSE));
===Die Terme schreiben wir noch etwas um, so dass man die Struktur hinter der virtuellen Formänderungsenergie erkennt - und erhalten:
- .===
Text
/* Element-Steifigkeitsmatrix K definieren */
K : makelist(makelist(coeff(
coeff(subst(VSE, δΠ[i]),q[2][m]),q[1][n]),
m,1,4),n,1,4);
print('δΠ[i],"=",k[i],"*",rest(q[2],-1),"*",
funmake('matrix,ratsimp(subst(simple,K/k[i]))),"*",
transpose(rest(q[1],-1)));
Post-Processing
Stabwerkskräfte und deren Knoten-Verschiebungen können wir nun mit geringem Aufwand bearbeiten:
Wir addieren die virtuelle Formänderungsenergie δΠi für jeden Stab zur gesamten virtuellen Formänderungsenergie δΠ zusammen.
Das wäre zwar anschaulich richtig - aber unpraktisch. So würden wir große Ausdrücke erhalten für δΠ. Einfacher und für die Behandlung mit dem Computer praktischer ist folgendes Vorgehen:
Ausgangspunkt ist die Element-Steifigkeitsmatrix
- .
Wir erzeugen uns eine Steifigkeitsmatrix für die Verschiebungen aller Knoten des Stabwerks und sortieren die Elemente der Element-Steifigkeitsmatrix sukzessive und additiv in diese ein.
Wie das geht, zeigt T313.
Links
- ...
Literature
- ...