Gelöste Aufgaben/PvV1: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 14: | Zeile 14: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:PvV1.png|alternativtext=|links|mini|205x205px|Lageplan]] | ||
Gesucht ist die erforderliche Haftkraft am Boden und ein Vorgehen nach dem Prinzip der virtuellen Verrückungen. | Gesucht ist die erforderliche Haftkraft am Boden und ein Vorgehen nach dem Prinzip der virtuellen Verrückungen. | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
==tmp== | ==tmp== | ||
[[Datei:PvV-11.png|mini|Koordinaten|alternativtext=|173x173px]] | |||
Hier ist die Leiter in Ihrer Referenzlage (grau) und in Ihrer variierten Lage eingezeichnet. Bei der Variation um ''δα'' wandert der Kraftangriffspunkt der Gewichtskraft ''G'' von ''C'' zu ''C''' nach oben. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Lagepan | {{MyCodeBlock|title=Lagepan | ||
|text=Text | |text=Text | ||
| Zeile 32: | Zeile 33: | ||
==tmp== | ==tmp== | ||
Die Verschiebungen der Kraftangriffspunkte von ''H'' und ''G'' sind ''u, v'': | |||
<math>\begin{pmatrix}\mathrm{u}\left( \alpha\right) =\mathrm{cos}\left( \alpha\right) \cdot \ell\\ \mathrm{v}\left( \alpha\right) =a\cdot \mathrm{sin}\left( \alpha\right) \end{pmatrix}</math> | |||
Für die Variation nutzen wir die dritte Koordinate α und ersetzen | |||
<math>\alpha \rightarrow \alpha+\varepsilon \cdot \delta \alpha</math> | |||
Zum Linearisieren führen wir die Hilfsgröße ε als Koeffizient von δα ein. Da die virtuelle Verrückung "differentiell klein" sein darf, nehmen wir nur das lineare Glied von | |||
<math>\displaystyle \frac{d}{d\varepsilon}(.)</math>. | |||
Damit erhalten wir die Variation von ''u'' und ''v'' zu: | |||
<math>\begin{pmatrix}\displaystyle \frac{d}{d\,\varepsilon}\cdot u \left( \varepsilon\cdot \mathit{\delta \alpha}+\alpha\right) =-\ell \cdot \mathit{\delta \alpha}\cdot \mathrm{sin}\left( \varepsilon\cdot \mathit{\delta \alpha}+\alpha\right) \\ \displaystyle \frac{d}{d\,\varepsilon}\cdot v\left( \epsilon\cdot \mathit{\delta \alpha}+\alpha\right) =a\cdot \mathit{\delta \alpha}\cdot \mathrm{cos}\left( \epsilon\cdot \mathit{\delta \alpha}+\alpha\right) \end{pmatrix} | |||
</math> | |||
und für ε=0: | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Kinematik | {{MyCodeBlock|title=Kinematik | ||
|text=Text | |text=Text | ||
| Zeile 42: | Zeile 63: | ||
==tmp== | ==tmp== | ||
In das Gleichgewicht gehen alle Arbeiten am System ein. | |||
Im Unterschied zu einem Kräftegleichgewicht fallen hier alle Lager-Reaktionskräfte herus: in A und B verschwindet nämlich das Skalarprodukt des virtuellen Verschiebungsvektors mit den Normalkräfte - sie stehen senkrecht aufeinander. | |||
Es bleiben: | |||
<math>\begin{array}{rl}\delta W =& -G\cdot \delta v - H \cdot \delta u \\ =&0 \end{array}</math> | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Gleichgewicht | {{MyCodeBlock|title=Gleichgewicht | ||
|text=Text | |text=Text | ||
| Zeile 52: | Zeile 81: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Mit der Gleichung oben haben wir genau eine Gleichung für ''H'' - das passt!. | ||
Allerdings haben wir drei Koordinaten ''u, v'' und α sowie deren Variationen. Die Forderung an die virtuellen Verrückungen ist jedoch, dass sie mit "der geometrischen Konfiguration des Systems verträglich". Die Leiter ist starr - wir haben also nur eine unabhängige Koordinate im System. Wir können und müssen also entweder | |||
* ''u'' und ''v'' durch α oder | |||
* ''u'' und α durch ''v'' oder | |||
* ''v'' und α durch ''u'' | |||
ausdrücken. <!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Gleichungen und Unbekannte abzählen | {{MyCodeBlock|title=Gleichungen und Unbekannte abzählen | ||
|text=Text | |text=Text | ||
| Zeile 62: | Zeile 100: | ||
==tmp== | ==tmp== | ||
Einsetzten der Variationen liefert | |||
<math>\sin\left( \alpha\right) \cdot \ell\cdot H\cdot \delta\alpha-a\cdot \cos\left( \alpha\right) \cdot G\cdot \delta\alpha=0</math> | |||
Charakteristisch ist dabei, dass sich die Variation - hier des Winkels α - herauskürzt: sie dient nur zur Identifikation einer Gleichung. Das wird wichtig, wenn wir mehrere Unbekannten und Koordinaten haben - dann ist der Koeffizient vor jeder Variation einer Koordinate ein Gleichgewichtsbeziehung. Jetzt macht die Aussage Sinn, dass sie "gedachte, voneinander unabhängige Verschiebungen" sind! | |||
Das Ergebnis für ''H'' ist: | |||
<math>\displaystyle H = \frac{a\cdot \mathrm{cos}\left( \alpha\right) \cdot G}{\mathrm{sin}\left( \alpha\right) \cdot \ell}</math> | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Lösen | {{MyCodeBlock|title=Lösen | ||
|text=Text | |text=Text | ||
| Zeile 72: | Zeile 121: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | [[Datei:PvV1-21.png|mini|Haftkraft ''H'']] | ||
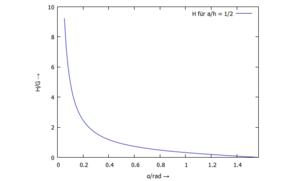
Beim Auftragen von H über α sehen wir: | |||
Die erforderliche Haftkraft wird sehr groß, wenn die Leiter flacher angestellt wird - das entspricht unserer Vorstellung.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Ausdeuten | {{MyCodeBlock|title=Ausdeuten | ||
|text=Text | |text=Text | ||
| Zeile 80: | Zeile 133: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
Version vom 1. April 2021, 12:45 Uhr
Aufgabenstellung
Hier übertragen wir das Lösungsschema der Statik auf den Lösungs-Ansatz mit dem Prinzip der virtuellen Verrückungen. Statt einem Freikörperbild müssen wir hier die Kinematik - also den Zusammenhang zwischen den Koordinaten des Systems - erfassen.
Dazu schauen wir uns dieses Problem an:
Ein Mann vom Gewicht G steht an der Stelle a auf einer Leiter der Länge ℓ (das Leitergewicht ist vernachlässigbar). Die Leiter ist unter dem Winkel α gegen die Wand geleht. Sie rollte oben an der Wand ab unten haftet sie am Boden.
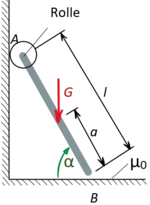
Gesucht ist die erforderliche Haftkraft am Boden und ein Vorgehen nach dem Prinzip der virtuellen Verrückungen.
Lösung mit Maxima
tmp
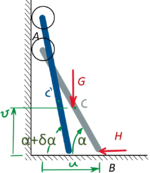
Hier ist die Leiter in Ihrer Referenzlage (grau) und in Ihrer variierten Lage eingezeichnet. Bei der Variation um δα wandert der Kraftangriffspunkt der Gewichtskraft G von C zu C' nach oben.
Lagepan
Text
1+1
tmp
Die Verschiebungen der Kraftangriffspunkte von H und G sind u, v:
Für die Variation nutzen wir die dritte Koordinate α und ersetzen
Zum Linearisieren führen wir die Hilfsgröße ε als Koeffizient von δα ein. Da die virtuelle Verrückung "differentiell klein" sein darf, nehmen wir nur das lineare Glied von
.
Damit erhalten wir die Variation von u und v zu:
und für ε=0:
Kinematik
Text
1+1
tmp
In das Gleichgewicht gehen alle Arbeiten am System ein.
Im Unterschied zu einem Kräftegleichgewicht fallen hier alle Lager-Reaktionskräfte herus: in A und B verschwindet nämlich das Skalarprodukt des virtuellen Verschiebungsvektors mit den Normalkräfte - sie stehen senkrecht aufeinander.
Es bleiben:
Gleichgewicht
Text
1+1
tmp
Mit der Gleichung oben haben wir genau eine Gleichung für H - das passt!.
Allerdings haben wir drei Koordinaten u, v und α sowie deren Variationen. Die Forderung an die virtuellen Verrückungen ist jedoch, dass sie mit "der geometrischen Konfiguration des Systems verträglich". Die Leiter ist starr - wir haben also nur eine unabhängige Koordinate im System. Wir können und müssen also entweder
- u und v durch α oder
- u und α durch v oder
- v und α durch u
ausdrücken.
Gleichungen und Unbekannte abzählen
Text
1+1
tmp
Einsetzten der Variationen liefert
Charakteristisch ist dabei, dass sich die Variation - hier des Winkels α - herauskürzt: sie dient nur zur Identifikation einer Gleichung. Das wird wichtig, wenn wir mehrere Unbekannten und Koordinaten haben - dann ist der Koeffizient vor jeder Variation einer Koordinate ein Gleichgewichtsbeziehung. Jetzt macht die Aussage Sinn, dass sie "gedachte, voneinander unabhängige Verschiebungen" sind!
Das Ergebnis für H ist:
Lösen
Text
1+1
tmp
Beim Auftragen von H über α sehen wir:
Die erforderliche Haftkraft wird sehr groß, wenn die Leiter flacher angestellt wird - das entspricht unserer Vorstellung.
Ausdeuten
Text
1+1
Links
- ...
Literature
- ...