Gelöste Aufgaben/LA01: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 16: | Zeile 16: | ||
Die Liste der produzierten Werkstücke erzeugen wir uns mit Matlab mit einer Zufalls-Funktion. | Die Liste der produzierten Werkstücke erzeugen wir uns mit Matlab mit einer Zufalls-Funktion. | ||
== Lösung mit | == Lösung mit Maxima== | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Title | |||
|text= | |||
Wir machen zwei Schritte zur Lösung: | Wir machen zwei Schritte zur Lösung: | ||
# die Formulierung des Problems als lineares Gleichungssystem, bei der wir nur die ersten drei Produktionstage berücksichtigen. | # die Formulierung des Problems als lineares Gleichungssystem, bei der wir nur die ersten drei Produktionstage berücksichtigen. | ||
# die Formulierung des Problems als "Gaußschen Methode der kleinsten Quadrate". | # die Formulierung des Problems als "Gaußschen Methode der kleinsten Quadrate". | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-10-16 */ | |||
/* ref: Lineare Gleichungssyteme in der Fertigung */ | |||
/* description: describe problem in terms of linear */ | |||
/* algebra and the least square method */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Declarations | ||
|text= | |text= | ||
Die vorgegebene Anzahl der je Werktag produzierten Werkstücke sei z.B.: | Die vorgegebene Anzahl der je Werktag produzierten Werkstücke sei z.B.: | ||
<math>\begin{array}{|c|r|r|} \hline &\;\;\;\;\;\; a & \;\;\;\;\;\;b\\ \hline \text{Tag 1:} &2&8\\\text{Tag 2:} & 11&2\\ \vdots& 15&0\\ & 10&3\\ &5&6\\ & 0&10\\ & 6&5\\ & 14&0\\ & 0&10\\ & 9&3\\ & 4&7\\ & 7&5\\ & 1&9\\\hline\end{array}</math> | ::<math>\begin{array}{|c|r|r|} \hline &\;\;\;\;\;\; a & \;\;\;\;\;\;b\\ \hline \text{Tag 1:} &2&8\\\text{Tag 2:} & 11&2\\ \vdots& 15&0\\ & 10&3\\ &5&6\\ & 0&10\\ & 6&5\\ & 14&0\\ & 0&10\\ & 9&3\\ & 4&7\\ & 7&5\\ & 1&9\\\hline\end{array}</math> | ||
Diese Liste erzeugen wir - bis auf die ersten drei - jeweils neu mit einer Zufallsvariablen in Excel. Die Ergebnisse sehen also jedes Mal etwas anders aus. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* Referenz-Lösung*/ | ||
P: [1/2, 3/4, 1/2]; | |||
/* aufgezeichnete Anzahl von Werkstücken */ | |||
n : [[(8- 1 - 8*P[2])/P[1],8], | |||
[(8- 1 - 2*P[2])/P[1],2], | |||
[(8-1/2- 0*P[2])/P[1],0]]; | |||
/* zufällige Liste für Werkstück a erzeugen */ | |||
data: makelist(random(15),i,1,10); | |||
timeleft: makelist( 8+1/2 | |||
-data[i]*P[1] | |||
-(if data[i]>0 then 1 else 0)*P[2],i,1,length(data)); | |||
data: makelist([data[i], | |||
if timeleft[i]>P[2]+P[3] then floor((timeleft[i]-P[3])/P[2]) else 0], | |||
i,1,length(data)); | |||
n : append(n,data); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Preparation | |||
|text= | |||
Wir brauchen ein '''Modell''' für den Produktionsprozess am Tag "''i''".[[Datei:LA01-11.png|mini|Phasenmodell|alternativtext=|525x525px]]Wir nehmen an, dass an jedem Tag zuerst die Werkstücke "a" (blau) und dann die Werkstücke "b" (grün) produziert werden. Wenn ein neues Werkstück produziert wird, muss die Maschine vorher eingerüstet werden. | Wir brauchen ein '''Modell''' für den Produktionsprozess am Tag "''i''".[[Datei:LA01-11.png|mini|Phasenmodell|alternativtext=|525x525px]]Wir nehmen an, dass an jedem Tag zuerst die Werkstücke "a" (blau) und dann die Werkstücke "b" (grün) produziert werden. Wenn ein neues Werkstück produziert wird, muss die Maschine vorher eingerüstet werden. | ||
Die Produktionsdauer für alle Werkstücke "a" am Tag ''i'' ist also | Die Produktionsdauer für alle Werkstücke "a" am Tag ''i'' ist also | ||
<math>T_{i,a} = N_{i,1}\cdot T_1</math> | ::<math>T_{i,a} = N_{i,1}\cdot T_1</math> | ||
mit der Anzahl der produzierten Werkstücke "a" von ''N<sub>i1</sub>''. | mit der Anzahl der produzierten Werkstücke "a" von ''N<sub>i1</sub>''. | ||
| Zeile 76: | Zeile 84: | ||
Wenn sowohl Werkstücke "a" als auch "b" produziert werden, erfordert dies zwei Rüstzeiten - sonst eine. Für die gesamte Rüstzeit je Tag gilt also: | Wenn sowohl Werkstücke "a" als auch "b" produziert werden, erfordert dies zwei Rüstzeiten - sonst eine. Für die gesamte Rüstzeit je Tag gilt also: | ||
<math>T_{i,R} = \left\{\begin{array}{cc} 2 \cdot T_3 & \text{ wenn } N_{i,1}>0 \text{ und } N_{i,2}>0 \\ 1 \cdot T_3 & \text{ sonst }\end{array} \right.</math>.[[Datei:LA01-12.png|mini|Tabelle erweitert um Rüstzeiten|alternativtext=|240x240px]]Wir erweitern deshalb unsere Tabelle um die Anzahl der Rüstzeiten je Tag und erhalten | ::<math>T_{i,R} = \left\{\begin{array}{cc} 2 \cdot T_3 & \text{ wenn } N_{i,1}>0 \text{ und } N_{i,2}>0 \\ 1 \cdot T_3 & \text{ sonst }\end{array} \right.</math>.[[Datei:LA01-12.png|mini|Tabelle erweitert um Rüstzeiten|alternativtext=|240x240px]]Wir erweitern deshalb unsere Tabelle um die Anzahl der Rüstzeiten je Tag und erhalten | ||
Für den ersten der ''I'' Tage lautet also die Gleichung für den Produktionsprozess: | Für den ersten der ''I'' Tage lautet also die Gleichung für den Produktionsprozess: | ||
<math>2\cdot T_1 + 8\cdot T_12+ 2\cdot T_3 = 8h</math>. | ::<math>2\cdot T_1 + 8\cdot T_12+ 2\cdot T_3 = 8h</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* include Rüstzeit */ | ||
n : makelist([n[i][1],n[i][2], | |||
(if n[i][1]>0 then 1 else 0)+ | |||
(if n[i][2]>0 then 1 else 0)],i,1,length(n)); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=First Approach | |||
|text= | |||
Wir können nun für jeden Tag eine lineare Gleichung wir oben formulieren. | Wir können nun für jeden Tag eine lineare Gleichung wir oben formulieren. | ||
Wir suchen allerdings nur drei Größen, nämlich | Wir suchen allerdings nur drei Größen, nämlich | ||
<math>\underline{t} = \left( \begin{array}{c}T_1\\T_2\\T_3\end{array}\right)</math> | ::<math>\underline{t} = \left( \begin{array}{c}T_1\\T_2\\T_3\end{array}\right)</math> | ||
Als ersten Ansatz nutzen wir die ersten drei Gleichungen und ignorieren zunächst die restlichen. Unser lineares Gleichungssystem sieht dann so aus: | Als ersten Ansatz nutzen wir die ersten drei Gleichungen und ignorieren zunächst die restlichen. Unser lineares Gleichungssystem sieht dann so aus: | ||
<math>\begin{pmatrix}2 & 8 & 2\\ 11 & 2 & 2\\ 15 & 0 & 1\end{pmatrix}\cdot\begin{pmatrix}{{T}_{1}}\\ {{T}_{2}}\\ {{T}_{3}}\end{pmatrix}=\begin{pmatrix}8\\ 8\\ 8\end{pmatrix}h</math>. | ::<math>\begin{pmatrix}2 & 8 & 2\\ 11 & 2 & 2\\ 15 & 0 & 1\end{pmatrix}\cdot\begin{pmatrix}{{T}_{1}}\\ {{T}_{2}}\\ {{T}_{3}}\end{pmatrix}=\begin{pmatrix}8\\ 8\\ 8\end{pmatrix}h</math>. | ||
Das Gleichungssystem hat eine Lösung, wenn die Determinante der ''3x3''-Matrix nicht Null ist (darum geben wir die ersten drei Listen-Elemente vor und lassen sie nicht durch einen Zufallsgenerator erzeugen ...). Die Lösung des Gleichungssystems lautet | Das Gleichungssystem hat eine Lösung, wenn die Determinante der ''3x3''-Matrix nicht Null ist (darum geben wir die ersten drei Listen-Elemente vor und lassen sie nicht durch einen Zufallsgenerator erzeugen ...). Die Lösung des Gleichungssystems lautet | ||
<math>\displaystyle {{T}_{1}}=\frac{1}{2} h, {{T}_{2}}=\frac{3}{4} h, {{T}_{3}}=\frac{1}{2} h</math>. | ::<math>\displaystyle {{T}_{1}}=\frac{1}{2} h, {{T}_{2}}=\frac{3}{4} h, {{T}_{3}}=\frac{1}{2} h</math>. | ||
Der Nachteil dieser Lösung: sie gilt für die ersten drei Gleichungen. Wie sieht es mit den anderen Gleichungen (Tagen) aus? wir berechnen den Fehler je Tag: | Der Nachteil dieser Lösung: sie gilt für die ersten drei Gleichungen. Wie sieht es mit den anderen Gleichungen (Tagen) aus? wir berechnen den Fehler je Tag: | ||
<math>\displaystyle [0,0,0,\frac{1}{4},0,0,-\frac{1}{4},-\frac{1}{2},0,-\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}] h</math> | ::<math>\displaystyle [0,0,0,\frac{1}{4},0,0,-\frac{1}{4},-\frac{1}{2},0,-\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}] h</math> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* gesuchte Größen */ | ||
t : transpose(makelist(T[j],j,1,3)); | |||
/* nur die ersten drei nehmen … */ | |||
print(funmake('matrix,([n[1],n[2],n[3]])),"∙",t,"=",transpose(r))$ | |||
sol: solve(makelist(n[i].t=r[i],i,1,3),[T[1],T[2],T[3]])[1]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Best Statistical Solution | |||
|text= | |||
Mit unserem ersten Ansatz müssen wir also für jeden Tag - außer den ersten dreien - mit einem Fehler in den ermittelten Bearbeitungsdauern ''T<sub>i</sub>'' rechnen. Was wir besser machen können: Wir fragen nach den Bearbeitungsdauern, | Mit unserem ersten Ansatz müssen wir also für jeden Tag - außer den ersten dreien - mit einem Fehler in den ermittelten Bearbeitungsdauern ''T<sub>i</sub>'' rechnen. Was wir besser machen können: Wir fragen nach den Bearbeitungsdauern, | ||
<math>\tilde{T}_i ,\;\; i=1,2,3</math> | ::<math>\tilde{T}_i ,\;\; i=1,2,3</math> | ||
die den Fehler im statistischen Mittel über alle Tage minimieren. | die den Fehler im statistischen Mittel über alle Tage minimieren. | ||
| Zeile 134: | Zeile 141: | ||
Grundlage dafür ist der Fehler ''e<sub>i</sub>'' je Tag, also | Grundlage dafür ist der Fehler ''e<sub>i</sub>'' je Tag, also | ||
<math>\displaystyle e_i = \sum_{j=1}^3 N_{i j}\cdot \tilde{T}_j - D_i \text{ mit } D_i = 8h</math>. | ::<math>\displaystyle e_i = \sum_{j=1}^3 N_{i j}\cdot \tilde{T}_j - D_i \text{ mit } D_i = 8h</math>. | ||
Damit nicht der Fehler an einem Tag den Fehler an einem anderen Tag numerisch kompensiert (also wenn z.B. ''e<sub>3</sub> + e<sub>17</sub> = 0''), sollen alle Fehler positiv eingehen. Statt den Betrag von ''e<sub>i</sub>'' zu verwenden, nimmt man ''e<sub>i<sup>2</sup></sub>'' (das Fehler-Quadrat) und erhält als Gesamtfehler-Funktion | Damit nicht der Fehler an einem Tag den Fehler an einem anderen Tag numerisch kompensiert (also wenn z.B. ''e<sub>3</sub> + e<sub>17</sub> = 0''), sollen alle Fehler positiv eingehen. Statt den Betrag von ''e<sub>i</sub>'' zu verwenden, nimmt man ''e<sub>i<sup>2</sup></sub>'' (das Fehler-Quadrat) und erhält als Gesamtfehler-Funktion | ||
<math>\displaystyle E\left(\tilde{T}_1,\tilde{T}_2,\tilde{T}_3\right) = \sum_{i=1}^I e_i^2</math>. | ::<math>\displaystyle E\left(\tilde{T}_1,\tilde{T}_2,\tilde{T}_3\right) = \sum_{i=1}^I e_i^2</math>. | ||
Diese Gesamtfehler-Funktion ist minimal, wenn | Diese Gesamtfehler-Funktion ist minimal, wenn | ||
<math>\displaystyle \frac{\partial E}{\partial \tilde{T}_j} = 0</math>. | ::<math>\displaystyle \frac{\partial E}{\partial \tilde{T}_j} = 0</math>. | ||
Numerisch mach es mehr Sinn, das Problem umzuformulieren. Dazu schreiben wir ''e<sub>i</sub>'' als | Numerisch mach es mehr Sinn, das Problem umzuformulieren. Dazu schreiben wir ''e<sub>i</sub>'' als | ||
<math>{{e}_{i}}\,=\,\frac{1}{2}\cdot \begin{pmatrix}{\tilde{T}_{1}}& {\tilde{T}_{2}}& {\tilde{T}_{3}}\end{pmatrix}\cdot \underbrace{ 2 \begin{pmatrix} {{N}_{i,1}^{2}} & {{N}_{i,1}}\cdot {{N}_{i,2}} & {{N}_{i,1}}\cdot {{N}_{i,3}}\\ {{N}_{i,1}}\cdot {{N}_{i,2}} & {{N}_{i,2}^{2}} & {{N}_{i,2}}\cdot {{N}_{i,3}}\\ {{N}_{i,1}}\cdot {{N}_{i,3}} & {{N}_{i,2}}\cdot {{N}_{i,3}} & {{N}_{i,3}^{2}} \end{pmatrix}}_{\displaystyle := \underline{\underline{A}}_i}\cdot \begin{pmatrix}{\tilde{T}_{1}}\\ {\tilde{T}_{2}}\\ {\tilde{T}_{3}}\end{pmatrix}+ \begin{pmatrix}{\tilde{T}_{1}}& {\tilde{T}_{2}}& {\tilde{T}_{3}}\end{pmatrix}\cdot \underbrace{\begin{pmatrix}-2{{D}_{i}}\cdot {{N}_{i,1}}\\ -2{{D}_{i}}\cdot {{N}_{i,2}}\\-2{{D}_{i}}\cdot {{N}_{i,3}}\end{pmatrix}}_{\displaystyle := \underline{b}_i} +{{D}_{i}^{2}}</math> | ::<math>{{e}_{i}}\,=\,\frac{1}{2}\cdot \begin{pmatrix}{\tilde{T}_{1}}& {\tilde{T}_{2}}& {\tilde{T}_{3}}\end{pmatrix}\cdot \underbrace{ 2 \begin{pmatrix} {{N}_{i,1}^{2}} & {{N}_{i,1}}\cdot {{N}_{i,2}} & {{N}_{i,1}}\cdot {{N}_{i,3}}\\ {{N}_{i,1}}\cdot {{N}_{i,2}} & {{N}_{i,2}^{2}} & {{N}_{i,2}}\cdot {{N}_{i,3}}\\ {{N}_{i,1}}\cdot {{N}_{i,3}} & {{N}_{i,2}}\cdot {{N}_{i,3}} & {{N}_{i,3}^{2}} \end{pmatrix}}_{\displaystyle := \underline{\underline{A}}_i}\cdot \begin{pmatrix}{\tilde{T}_{1}}\\ {\tilde{T}_{2}}\\ {\tilde{T}_{3}}\end{pmatrix}+ \begin{pmatrix}{\tilde{T}_{1}}& {\tilde{T}_{2}}& {\tilde{T}_{3}}\end{pmatrix}\cdot \underbrace{\begin{pmatrix}-2{{D}_{i}}\cdot {{N}_{i,1}}\\ -2{{D}_{i}}\cdot {{N}_{i,2}}\\-2{{D}_{i}}\cdot {{N}_{i,3}}\end{pmatrix}}_{\displaystyle := \underline{b}_i} +{{D}_{i}^{2}}</math> | ||
und damit | und damit | ||
<math>\displaystyle E = \frac{1}{2} \cdot \underline{\tilde{t}}^T \underline{\underline{A}}\cdot \underline{\tilde{t}} + \underline{\tilde{t}}^T \underline{b} + c</math>. | ::<math>\displaystyle E = \frac{1}{2} \cdot \underline{\tilde{t}}^T \underline{\underline{A}}\cdot \underline{\tilde{t}} + \underline{\tilde{t}}^T \underline{b} + c</math>. | ||
Dann ist | Dann ist | ||
<math>\displaystyle \underline{\underline{A}}=\sum_{i=1}^I \underline{\underline{A}}_i ,\;\; \underline{b}=\sum_{i=1}^I \underline{b}_i \text{ und } c = I \cdot D_i^2</math>. | ::<math>\displaystyle \underline{\underline{A}}=\sum_{i=1}^I \underline{\underline{A}}_i ,\;\; \underline{b}=\sum_{i=1}^I \underline{b}_i \text{ und } c = I \cdot D_i^2</math>. | ||
Mit unseren Zahlen finden wir | Mit unseren Zahlen finden wir | ||
<math>\displaystyle \underline{\underline{A}}= \begin{pmatrix}1708 & 454 & 278\\ 454 & 1004 & 232\\ 278 & 232 & 80\end{pmatrix} \;\; \underline{b}= \begin{pmatrix}-1344\\ -1088\\ -352\end{pmatrix} h \text{ und } c = 832 h^2</math>. | ::<math>\displaystyle \underline{\underline{A}}= \begin{pmatrix}1708 & 454 & 278\\ 454 & 1004 & 232\\ 278 & 232 & 80\end{pmatrix} \;\; \underline{b}= \begin{pmatrix}-1344\\ -1088\\ -352\end{pmatrix} h \text{ und } c = 832 h^2</math>. | ||
Aus dem Abschnitt Minimum Prinzipe kennen wir die Struktur der Gesamtfehler-Funktion - wir können deshalb den Lösungs-Algorithmus für das Minimum-Problem von dort übernehmen und erhalten aus | Aus dem Abschnitt Minimum Prinzipe kennen wir die Struktur der Gesamtfehler-Funktion - wir können deshalb den Lösungs-Algorithmus für das Minimum-Problem von dort übernehmen und erhalten aus | ||
<math>\underline{\underline{A}} \cdot \underline{\tilde{t}} = -\underline{b}</math> | ::<math>\underline{\underline{A}} \cdot \underline{\tilde{t}} = -\underline{b}</math> | ||
die Losung | die Losung | ||
<math>\tilde{T}_1 = 0.52 h, \;\tilde{T}_2 = 0.76 h, \;\tilde{T}_3 = 0.38 h</math>.< | ::<math>\tilde{T}_1 = 0.52 h, \;\tilde{T}_2 = 0.76 h, \;\tilde{T}_3 = 0.38 h</math>. | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* define error function */ | |||
row: e[i]=(sum(N[i,j]*T[j],j,1,3)-D[i])^2; | |||
row : expand(subst(row,e[i])); | |||
null: makelist(T[j]=0,j,1,3); | |||
c : subst(null,row); | |||
row: row-c; | |||
b : subst(null,makelist(coeff(row,T[j],1),j,1,3)); | |||
row: row-b.t; | |||
load(diag)$ | |||
A : 1/2*makelist(coeff(makelist(coeff(row,T[j],1),j,1,3),T[k]),k,1,3) | |||
+ diag(makelist(coeff(row,T[j],2),j,1,3)); | |||
row: expand(row-transpose(t).A.t); | |||
print(e[i]," = ", 1/2,transpose(t),"∙2",A,"∙",t,"+",transpose(t),"∙",transpose(b),"+",c)$ | |||
Alpha : [[0,0,0],[0,0,0],[0,0,0]]; | |||
Beta : [0,0,0]; | |||
Alpha : 2*sum(subst([N[i,1]=n[j][1],N[i,2]=n[j][2],N[i,3]=n[j][3]],A),j,1,length(n)); | |||
Beta : sum(subst([N[i,1]=n[j][1],N[i,2]=n[j][2],N[i,3]=n[j][3], D[i]=8],b),j,1,length(n)); | |||
{{MyCodeBlock|title= | sol: [sol,solve(makelist(Alpha[j].t + Beta[j]=0,j,1,3),[T[1],T[2],T[3]])[1]] | ||
|text= | </syntaxhighlight> | ||
}} | |||
{{MyCodeBlock|title=Lösung mit Matlab | |||
|text=Dazu gibt es auch ein Skript zur Bearbeitung mit Matlab. Das wird näher in | |||
* [[Werkzeuge/Software/Matlab/Grundstruktur_eines_Matlab©-Programms|Grundstruktur_eines_Matlab©-Programms]] | |||
beschreiben. | |||
|code= | |code= | ||
<syntaxhighlight lang=" | <syntaxhighlight lang="Matlab" line start=1> | ||
1 | % MATLAB script % | ||
% version: wxMaxima R2015a % | |||
% author: Andreas Baumgart % | |||
% last updated: 2018-11-01 % | |||
% elfe-platform.atlassian.net/wiki/spaces/TTM/pages/821362915/LA01 % | |||
% description: find best statistical production % | |||
% durations for % | |||
% workpiece "a", "b" and setup-time % | |||
% ***************************************************** % | |||
% look in "Functions" for functions | |||
addpath('Functions'); | |||
%% Step 1: Pre-Process % | |||
% read from file | |||
fileName = 'records.xlsx'; | |||
[data, D, A, b, c] = preProcess(fileName); | |||
%% Step 2: Solve % | |||
t = linsolve(A,-b); | |||
%% Step 3: Post-Process | |||
postProcess(data, D, t); | |||
%% END % | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
{{MySpreadsheetBlock|title=Messwerte|text=Die "Messwerte" für die Bearbeitung mit Matlab erzeugen wir - bis auf die ersten drei - jeweils neu mit einer Zufallsvariablen in Excel. | |||
[[Datei:LA01-21.png|mini|Fehlerfunktion|ohne]]Die Ergebnisse sehen also jedes Mal etwas anders aus; z.B. so: |file=LA01.xlsx}} | |||
<hr/> | <hr/> | ||
'''Links''' | '''Links''' | ||
* | * [[Werkzeuge/Software/Matlab/Grundstruktur_eines_Matlab©-Programms|Grundstruktur_eines_Matlab©-Programms]] | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Version vom 1. April 2021, 06:55 Uhr
Aufgabenstellung
Hier unternehmen wir einen Ausflug in die - und ihre Verbindung zu Minimalprinzipen und der .
Dabei sollen Parameter eines Produktions-Systems indentifiziert werden.
Eine Maschine produziert die Werkstücke "a" und "b" in einer 8h-Schicht. Die Anzahl der produzierten Werkstücke ist gegeben. Die Rüstzeit für beide Werkstücke an der Maschine sei gleich.
Gesucht ist die Bearbeitungsdauern jeweils für Werkstück a und b. Die Liste der produzierten Werkstücke erzeugen wir uns mit Matlab mit einer Zufalls-Funktion.
Lösung mit Maxima
Title
Wir machen zwei Schritte zur Lösung:
- die Formulierung des Problems als lineares Gleichungssystem, bei der wir nur die ersten drei Produktionstage berücksichtigen.
- die Formulierung des Problems als "Gaußschen Methode der kleinsten Quadrate".
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-10-16 */
/* ref: Lineare Gleichungssyteme in der Fertigung */
/* description: describe problem in terms of linear */
/* algebra and the least square method */
/*******************************************************/
Declarations
Die vorgegebene Anzahl der je Werktag produzierten Werkstücke sei z.B.:
Diese Liste erzeugen wir - bis auf die ersten drei - jeweils neu mit einer Zufallsvariablen in Excel. Die Ergebnisse sehen also jedes Mal etwas anders aus.
/* Referenz-Lösung*/
P: [1/2, 3/4, 1/2];
/* aufgezeichnete Anzahl von Werkstücken */
n : [[(8- 1 - 8*P[2])/P[1],8],
[(8- 1 - 2*P[2])/P[1],2],
[(8-1/2- 0*P[2])/P[1],0]];
/* zufällige Liste für Werkstück a erzeugen */
data: makelist(random(15),i,1,10);
timeleft: makelist( 8+1/2
-data[i]*P[1]
-(if data[i]>0 then 1 else 0)*P[2],i,1,length(data));
data: makelist([data[i],
if timeleft[i]>P[2]+P[3] then floor((timeleft[i]-P[3])/P[2]) else 0],
i,1,length(data));
n : append(n,data);
Preparation
Wir brauchen ein Modell für den Produktionsprozess am Tag "i".

Wir nehmen an, dass an jedem Tag zuerst die Werkstücke "a" (blau) und dann die Werkstücke "b" (grün) produziert werden. Wenn ein neues Werkstück produziert wird, muss die Maschine vorher eingerüstet werden.
Die Produktionsdauer für alle Werkstücke "a" am Tag i ist also
mit der Anzahl der produzierten Werkstücke "a" von Ni1.
Gleiches gilt für die Werkstücke "b".
Wenn sowohl Werkstücke "a" als auch "b" produziert werden, erfordert dies zwei Rüstzeiten - sonst eine. Für die gesamte Rüstzeit je Tag gilt also:
Für den ersten der I Tage lautet also die Gleichung für den Produktionsprozess:
- .
/* include Rüstzeit */
n : makelist([n[i][1],n[i][2],
(if n[i][1]>0 then 1 else 0)+
(if n[i][2]>0 then 1 else 0)],i,1,length(n));
First Approach
Wir können nun für jeden Tag eine lineare Gleichung wir oben formulieren.
Wir suchen allerdings nur drei Größen, nämlich
Als ersten Ansatz nutzen wir die ersten drei Gleichungen und ignorieren zunächst die restlichen. Unser lineares Gleichungssystem sieht dann so aus:
- .
Das Gleichungssystem hat eine Lösung, wenn die Determinante der 3x3-Matrix nicht Null ist (darum geben wir die ersten drei Listen-Elemente vor und lassen sie nicht durch einen Zufallsgenerator erzeugen ...). Die Lösung des Gleichungssystems lautet
- .
Der Nachteil dieser Lösung: sie gilt für die ersten drei Gleichungen. Wie sieht es mit den anderen Gleichungen (Tagen) aus? wir berechnen den Fehler je Tag:
/* gesuchte Größen */
t : transpose(makelist(T[j],j,1,3));
/* nur die ersten drei nehmen … */
print(funmake('matrix,([n[1],n[2],n[3]])),"∙",t,"=",transpose(r))$
sol: solve(makelist(n[i].t=r[i],i,1,3),[T[1],T[2],T[3]])[1];
Best Statistical Solution
Mit unserem ersten Ansatz müssen wir also für jeden Tag - außer den ersten dreien - mit einem Fehler in den ermittelten Bearbeitungsdauern Ti rechnen. Was wir besser machen können: Wir fragen nach den Bearbeitungsdauern,
die den Fehler im statistischen Mittel über alle Tage minimieren.
Grundlage dafür ist der Fehler ei je Tag, also
- .
Damit nicht der Fehler an einem Tag den Fehler an einem anderen Tag numerisch kompensiert (also wenn z.B. e3 + e17 = 0), sollen alle Fehler positiv eingehen. Statt den Betrag von ei zu verwenden, nimmt man ei2 (das Fehler-Quadrat) und erhält als Gesamtfehler-Funktion
- .
Diese Gesamtfehler-Funktion ist minimal, wenn
- .
Numerisch mach es mehr Sinn, das Problem umzuformulieren. Dazu schreiben wir ei als
und damit
- .
Dann ist
- .
Mit unseren Zahlen finden wir
- .
Aus dem Abschnitt Minimum Prinzipe kennen wir die Struktur der Gesamtfehler-Funktion - wir können deshalb den Lösungs-Algorithmus für das Minimum-Problem von dort übernehmen und erhalten aus
die Losung
- .
/* define error function */
row: e[i]=(sum(N[i,j]*T[j],j,1,3)-D[i])^2;
row : expand(subst(row,e[i]));
null: makelist(T[j]=0,j,1,3);
c : subst(null,row);
row: row-c;
b : subst(null,makelist(coeff(row,T[j],1),j,1,3));
row: row-b.t;
load(diag)$
A : 1/2*makelist(coeff(makelist(coeff(row,T[j],1),j,1,3),T[k]),k,1,3)
+ diag(makelist(coeff(row,T[j],2),j,1,3));
row: expand(row-transpose(t).A.t);
print(e[i]," = ", 1/2,transpose(t),"∙2",A,"∙",t,"+",transpose(t),"∙",transpose(b),"+",c)$
Alpha : [[0,0,0],[0,0,0],[0,0,0]];
Beta : [0,0,0];
Alpha : 2*sum(subst([N[i,1]=n[j][1],N[i,2]=n[j][2],N[i,3]=n[j][3]],A),j,1,length(n));
Beta : sum(subst([N[i,1]=n[j][1],N[i,2]=n[j][2],N[i,3]=n[j][3], D[i]=8],b),j,1,length(n));
sol: [sol,solve(makelist(Alpha[j].t + Beta[j]=0,j,1,3),[T[1],T[2],T[3]])[1]]
Lösung mit Matlab
Dazu gibt es auch ein Skript zur Bearbeitung mit Matlab. Das wird näher in
beschreiben.
% MATLAB script %
% version: wxMaxima R2015a %
% author: Andreas Baumgart %
% last updated: 2018-11-01 %
% elfe-platform.atlassian.net/wiki/spaces/TTM/pages/821362915/LA01 %
% description: find best statistical production %
% durations for %
% workpiece "a", "b" and setup-time %
% ***************************************************** %
% look in "Functions" for functions
addpath('Functions');
%% Step 1: Pre-Process %
% read from file
fileName = 'records.xlsx';
[data, D, A, b, c] = preProcess(fileName);
%% Step 2: Solve %
t = linsolve(A,-b);
%% Step 3: Post-Process
postProcess(data, D, t);
%% END %
Messwerte
Die "Messwerte" für die Bearbeitung mit Matlab erzeugen wir - bis auf die ersten drei - jeweils neu mit einer Zufallsvariablen in Excel.
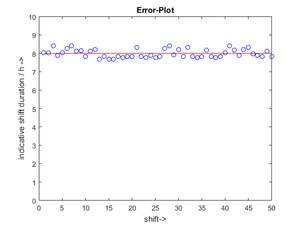
Die Ergebnisse sehen also jedes Mal etwas anders aus; z.B. so:

download spreadsheet →
Links
Literature
- ...
