Gelöste Aufgaben/Kw99

Aufgabenstellung

Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten q_A in A und q_B in B sowie dem Moment M_B in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l₁ bzw. l₂ sowie den Flächenmomenten I₁ bzw. I₂. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit K_A, die Federn in B und C sind Translationsfedern mit den Steifigkeiten k_B, k_C.

Lageplan

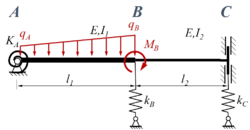
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken. Im Vergleich zu Kw98 wird hier eine Lösung mit normierten Koordinaten versucht.

Systemparameter

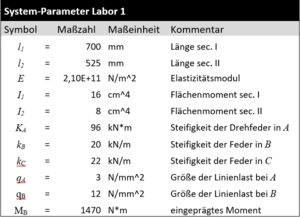
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:

Lösung mit Maxima

Die Aufgabe ist ein klassisches Randwertproblem:

1. zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehung

   $E\;I_{i}w_{i}^{IV}(x_{i})=q(x_{i}),\;\;i=\{1,2\}$

   berschrieben wird.
2. Rand- und Übergangsbedingungen in den Punkten A, B, C

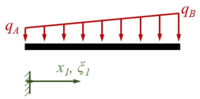
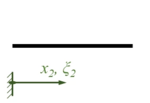
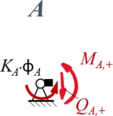
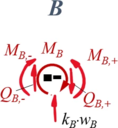
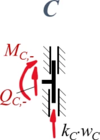
Wir verwenden x_i und ξ_i als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:

Rand A	Bereich I	Übergang B	Bereich II	Rand C

Header

Diese Aufgabe mit der Methode der Finiten Elemente in KW96 gelöst. Und im Vergleich zu KW98 wird hier die analytische Lösung mit dimensionslosen Koordinaten angeschreiben.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2017-09-06                            */
/* ref: TM-C, Labor 1 - dimensionslos                  */
/* description: die Auslenkung w und die unabhängige   */
/*              Ortskoordinate werden dim'los gemacht  */
/*******************************************************/

Declarations

Wir definieren die Formfunktionen für die Streckenlast

${\begin{array}{l}{{\phi }_{0}}\left(\xi \right):=1-\xi \\{{\phi }_{1}}\left(\xi \right):=\xi \end{array}}{\text{ mit }}\xi =\displaystyle {\frac {x_{1}}{\ell _{1}}}$.

/* system parameter */
params: [EI[2]=EI[1]/2,
         K[A]=EI[1]/l[1],
         k[B]=0,
         k[C] = EI[1]/l[1]^3,
         q[B]=4*q[A],
         l[2]=l[1]/2,
         M[B] = 5*q[A]*l[1]^2];

/* form - functions  */
phi[0](xi) := 1 - xi;
phi[1](xi) :=     xi;

/* system parameter */ params: [EI[2]=EI[1]/2,

        K[A]=EI[1]/l[1],
        k[B]=0,
        k[C] = EI[1]/l[1]^3,
        q[B]=4*q[A],
        l[2]=l[1]/2,
        M[B] = 5*q[A]*l[1]^2];

/* form - functions */ phi[0](xi) := 1 - xi; phi[1](xi) := xi;

Formfunctions

Y

Y

Für die 2*4 = 8 Integrationskonstanten

$\left[C_{1,0},C_{1,1},C_{1,2},C_{1,3},C_{2,0},C_{2,1},C_{2,2},C_{2,3}\right]$

suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen.

Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen.

Aus Rand "A"

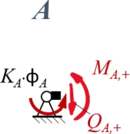
Geometrische Randbedingungen $w_{1}(0)=0$ Kraft- und Momenten-Randbedingungen $K_{A}\cdot \phi _{A}+M_{A,+}=0{\text{ mit }}M_{A,+}=-EI_{1}\cdot w''(x)|_{x=0}$

Aus Übergang "B"

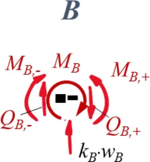
Geometrische Randbedingungen $w_{1}(\ell _{1})=w_{2}(\ell _{1})$ $\phi _{1}(\ell _{1})=\phi _{2}(\ell _{1})$ Kraft- und Momenten-Randbedingungen $-M_{B,-}-M_{B}+M_{B,+}=0$ $-Q_{B,-}-k_{B}\cdot w_{B}+-Q_{B,+}=0$

Aus Rand "C"

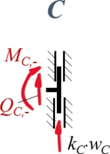
Geometrische Randbedingungen $\phi _{2}(\ell _{2})=0$ Kraft- und Momenten-Randbedingungen $-Q_{C,-}-k_{C}\cdot w_{C}=0$

Und das liefert das Gleichungssystem aus 8 Gleichungen

${\begin{pmatrix}{\frac {{C}_{1,0}}{{\mathit {EI}}_{1}}}=0\\{\frac {{{C}_{1,1}}\cdot {{K}_{A}}}{{\mathit {EI}}_{1}}}-{{C}_{1,2}}=0\\{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{B}}}{120\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{A}}}{30\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{3}}\cdot {{C}_{1,3}}}{6\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{2}}\cdot {{C}_{1,2}}}{2\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}}\cdot {{C}_{1,1}}}{{\mathit {EI}}_{1}}}+{\frac {{C}_{1,0}}{{\mathit {EI}}_{1}}}={\frac {{C}_{2,0}}{{\mathit {EI}}_{2}}}\\{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{B}}}{24\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{A}}}{8\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{2}}\cdot {{C}_{1,3}}}{2\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}}\cdot {{C}_{1,2}}}{{\mathit {EI}}_{1}}}+{\frac {{C}_{1,1}}{{\mathit {EI}}_{1}}}={\frac {{C}_{2,1}}{{\mathit {EI}}_{2}}}\\{\frac {{{\ell }_{1}}\cdot {{q}_{B}}}{2}}-{\frac {{{C}_{2,0}}\cdot {{k}_{B}}}{{\mathit {EI}}_{2}}}+{\frac {{{\ell }_{1}}\cdot {{q}_{A}}}{2}}-{{C}_{2,3}}+{{C}_{1,3}}=0\\-{{M}_{B}}+{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{B}}}{6}}+{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{A}}}{3}}-{{C}_{2,2}}+{{\ell }_{1}}\cdot {{C}_{1,3}}+{{C}_{1,2}}=0\\{\frac {{{\ell }_{2}^{2}}\cdot {{C}_{2,3}}}{2\cdot {{\mathit {EI}}_{2}}}}+{\frac {{{\ell }_{2}}\cdot {{C}_{2,2}}}{{\mathit {EI}}_{2}}}+{\frac {{C}_{2,1}}{{\mathit {EI}}_{2}}}=0\\-{\frac {{{\ell }_{2}^{3}}\cdot {{C}_{2,3}}\cdot {{k}_{C}}}{6\cdot {{\mathit {EI}}_{2}}}}-{\frac {{{\ell }_{2}^{2}}\cdot {{C}_{2,2}}\cdot {{k}_{C}}}{2\cdot {{\mathit {EI}}_{2}}}}-{\frac {{{\ell }_{2}}\cdot {{C}_{2,1}}\cdot {{k}_{C}}}{{\mathit {EI}}_{2}}}-{\frac {{{C}_{2,0}}\cdot {{k}_{C}}}{{\mathit {EI}}_{2}}}+{{C}_{2,3}}=0\end{pmatrix}}$

für die Integrationskonstanten.

Boundary Conditions

1+1

Prepare for Solver

Das Gleichungssystem wollen wir als

${\underline {\underline {A}}}\cdot {\underline {x}}={\underline {b}}$

schreiben, also

Fehler beim Parsen (Unbekannte Funktion „\begin{pmatrix}“): {\displaystyle \begin{pmatrix}\frac{1}{{{\mathit{EI}}_{1}}} & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & \frac{{{K}_{A}}}{{{\mathit{EI}}_{1}}} & -1 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{{{\mathit{EI}}_{1}}} & \frac{{{\ell}_{{MyCodeBlock|title=Prepare for Solver |text= Das Gleichungssystem wollen wir als ::<math>\underline{\underline{A}}\cdot\underline{x}= \underline{b}}

schreiben, also

Fehler beim Parsen (Unbekannte Funktion „\begin{pmatrix}“): {\displaystyle \begin{pmatrix}\frac{1}{{{\mathit{EI}}_{1}}} & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & \frac{{{K}_{A}}}{{{\mathit{EI}}_{1}}} & -1 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{{{\mathit{EI}}_{1}}} & \frac{{{\ell}_{{MyCodeBlock|title=Prepare for Solver |text= Das Gleichungssystem wollen wir als ::<math>\underline{\underline{A}}\cdot\underline{x}= \underline{b}}

schreiben, also

${\begin{pmatrix}{\frac {1}{{\mathit {EI}}_{1}}}&0&0&0&0&0&0&0\\0&{\frac {{K}_{A}}{{\mathit {EI}}_{1}}}&-1&0&0&0&0&0\\{\frac {1}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}^{2}}{2\cdot {{\mathit {EI}}_{1}}}}&{\frac {{\ell }_{1}^{3}}{6\cdot {{\mathit {EI}}_{1}}}}&-{\frac {1}{{\mathit {EI}}_{2}}}&0&0&0\\0&{\frac {1}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}^{2}}{2\cdot {{\mathit {EI}}_{1}}}}&0&-{\frac {1}{{\mathit {EI}}_{2}}}&0&0\\0&0&0&1&-{\frac {{k}_{B}}{{\mathit {EI}}_{2}}}&0&0&-1\\0&0&1&{{\ell }_{1}}&0&0&-1&0\\0&0&0&0&0&{\frac {1}{{\mathit {EI}}_{2}}}&{\frac {{\ell }_{2}}{{\mathit {EI}}_{2}}}&{\frac {{\ell }_{2}^{2}}{2\cdot {{\mathit {EI}}_{2}}}}\\0&0&0&0&-{\frac {{k}_{C}}{{\mathit {EI}}_{2}}}&-{\frac {{{\ell }_{2}}\cdot {{k}_{C}}}{{\mathit {EI}}_{2}}}&-{\frac {{{\ell }_{2}^{2}}\cdot {{k}_{C}}}{2\cdot {{\mathit {EI}}_{2}}}}&-{\frac {{{\ell }_{2}^{3}}\cdot {{k}_{C}}-6\cdot {{\mathit {EI}}_{2}}}{6\cdot {{\mathit {EI}}_{2}}}}\end{pmatrix}}\cdot {\underline {x}}={\begin{pmatrix}0\\0\\-{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{B}}}{120\cdot {{\mathit {EI}}_{1}}}}-{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{A}}}{30\cdot {{\mathit {EI}}_{1}}}}\\-{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{B}}}{24\cdot {{\mathit {EI}}_{1}}}}-{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{A}}}{8\cdot {{\mathit {EI}}_{1}}}}\\-{\frac {{{\ell }_{1}}\cdot {{q}_{B}}}{2}}-{\frac {{{\ell }_{1}}\cdot {{q}_{A}}}{2}}\\{{M}_{B}}-{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{B}}}{6}}-{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{A}}}{3}}\\0\\0\end{pmatrix}}$

Die Matrix-Elemente sind für die Koeffizientenmatrix

${\begin{array}{l}a_{1,1}=1/EI_{1}\\a_{2,2}=K_{A}/EI_{1}\\a_{2,3}=-1\\a_{3,1}=1/EI_{1}\\a_{3,2}=\ell _{1}/EI_{1}\\a_{3,3}=\ell _{1}^{2}/(2\cdot EI_{1})\\a_{3,4}=\ell _{1}^{3}/(6\cdot EI_{1})\\a_{3,5}=-1/EI_{2}\\a_{4,2}=1/EI_{1}\\a_{4,3}=\ell _{1}/EI_{1}\\a_{4,4}=\ell _{1}^{2}/(2\cdot EI_{1})\\a_{4,6}=-1/EI_{2}\\a_{5,4}=1\\a_{5,5}=-k_{B}/EI_{2}\\a_{5,8}=-1\\a_{6,3}=1\\a_{6,4}=\ell _{1}\\a_{6,7}=-1\\a_{7,6}=1/EI_{2}\\a_{7,7}=\ell _{2}/EI_{2}\\a_{7,8}=\ell _{2}^{2}/(2\cdot EI_{2})\\a_{8,5}=-k_{C}/EI_{2}\\a_{8,6}=-(\ell _{2}\cdot k_{C})/EI_{2}\\a_{8,7}=-(\ell _{2}^{2}\cdot k_{C})/(2\cdot EI_{2})\\a_{8,8}=-(\ell _{2}^{3}\cdot k_{C}-6\cdot EI_{2})/(6\cdot EI_{2})\\\end{array}}$

und für die rechte Seite

${\begin{array}{l}b_{1}=0\\b_{2}=0\\b_{3}=(-(\ell _{1}^{4}\cdot q_{B})/(120\cdot EI_{1}))-(\ell _{1}^{4}\cdot q_{A})/(30\cdot EI_{1})\\b_{4}=(-(\ell _{1}^{3}\cdot q_{B})/(24\cdot EI_{1}))-(\ell _{1}^{3}\cdot q_{A})/(8\cdot EI_{1})\\b_{5}=(-(\ell _{1}\cdot q_{B})/2)-(\ell _{1}\cdot q_{A})/2\\b_{6}=M_{B}-(\ell _{1}^{2}\cdot q_{B})/6-(\ell _{1}^{2}\cdot q_{A})/3\\b_{7}=0\\b_{8}=0\end{array}}$.

/* augmented coeff matrix */
ACM: augcoefmatrix(BCs,ICs);
AA :   submatrix(ACM,9);
bb : - col(ACM,9);

for i: 1 thru 8 do
   print(simplode(["b[",i,"] = ", string(bb[i][1])]))$
for i: 1 thru 8 do
   for j: 1 thru 8 do
      if not AA[i][j] = 0 then
          print(simplode(["A[",i,",",j,"] = ", string(AA[i][j])]))$

Solving

Das Lösen des Gleichungssystems liefert

${\begin{array}{l}{{C}_{1,0}}=0,\\{{C}_{1,1}}=246.1\;N{{m}^{2}},\\{{C}_{1,2}}=703.2\;Nm,\\{{C}_{1,3}}=-2404.3\;N,\\{{C}_{2,0}}=127.6\;Nm^{3},\\{{C}_{2,1}}=224.7\;Nm^{2},\\{{C}_{2,2}}=-979.8\;Nm,\\{{C}_{2,3}}=2101.8N\end{array}}$.

1+1

Post-Processing

Und die Ergebnisse können wir uns anschauen ...

... für w(x):

Biegelinie w(x)

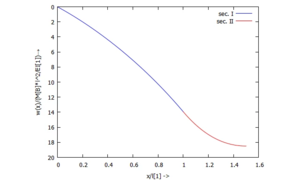
... für Φ(x):

Kippung w'(x)

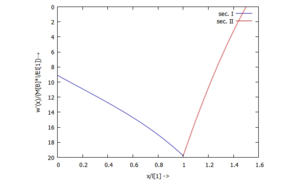
... für M(x):

Biegemoment M(x)

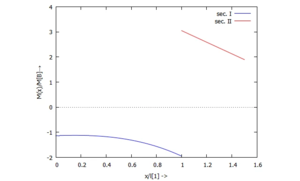
... für Q(x):

Querkraft Q(x)

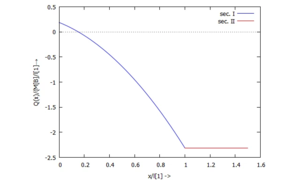
... für die Lager-Reaktionskräfte:

${\begin{array}{ll}{{A}_{z}}&={\frac {257\cdot {{\ell }_{1}}\cdot {{q}_{A}}}{1365}},\\{{M}_{A}}&={\frac {1331\cdot {{\ell }_{1}^{2}}\cdot {{q}_{A}}}{1170}},\\{{B}_{z}}&=0,\\{{C}_{z}}&={\frac {6311\cdot {{\ell }_{1}}\cdot {{q}_{A}}}{2730}},\\{{M}_{C}}&={\frac {31037\cdot {{\ell }_{1}^{2}}\cdot {{q}_{A}}}{16380}}\end{array}}$

/* bearing forces and moments */
reactForces: [A[z] = Q[1](0),
              M[A] = K[A]*Phi[1](0),
              B[z] = k[B]*w[2](0),
              C[z] = k[C]*w[2](1),
              M[C] = M[2](1)];

expand(subst(dimless,subst(params,subst(sol, reactForces))));

/* plot displacements */

fcts: [[ w [1](xi), w [2](xi)],
       [Phi[1](xi),Phi[2](xi)],
       [ M [1](xi), M [2](xi)],
       [ Q [1](xi), Q [2](xi)]];
facts: [1/l[Bez], l[1]/l[Bez], 1/(q[A]*l[1]^2), 1/(q[A]*l[1])];

textlabels : ["w(x)/(M[B]*l^2/EI[1])→", "w'(x)/(M[B]*l/EI[1])→", "M(x)/M[B]→", "Q(x)/(M[B]/l[1]→"];
for i: 1 thru 4 do(
  f : expand(subst(dimless,subst(params,facts[i]*[subst(sol, fcts[i][1]),
                                                  subst(sol, fcts[i][2])]))),
  r : subst(params,l[2]/l[1]),                                          
  preamble: if i<=2 then "set yrange [] reverse" else "set yrange []",
  plot2d([[parametric,     t, subst(t,xi,f[1]), [t,0,1]],
          [parametric, 1+r*t, subst(t,xi,f[2]), [t,0,1]]],
                             [legend, "sec. I", "sec. II"],
                             [gnuplot_preamble, preamble],
                             [xlabel, "x/l[1] ->"],
                             [ylabel, textlabels[i]]))$

---

Links

• ...

Literature

• ...