Gelöste Aufgaben/Kw98

Aufgabenstellung

Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten q_A in A und q_B in B sowie dem Moment M_B in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l₁ bzw. l₂ sowie den Flächenmomenten I₁ bzw. I₂. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit K_A, die Federn in B und C sind Translationsfedern mit den Steifigkeiten k_B, k_C.

Lageplan

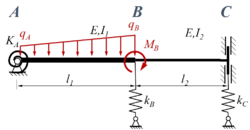
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken.

Systemparameter

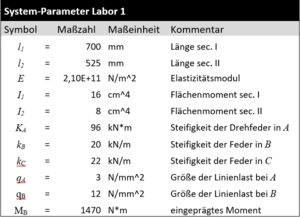
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:

Lösung mit Maxima

Die Aufgabe ist ein klassisches Randwertproblem:

1. zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehung

   $E\;I_{i}w_{i}^{IV}(x_{i})=q(x_{i}),\;\;i=\{1,2\}$

   berschrieben wird.
2. Rand- und Übergangsbedingungen in den Punkten A, B, C

Wir verwenden x_i und ξ_i als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:

Rand A	Bereich I	Übergang B	Bereich II	Rand C

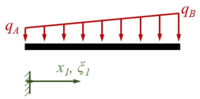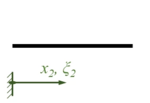Header

Diese Aufgabe mit der Methode der Finiten Elemente in KW96 gelöst.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2017-09-06                            */
/* ref: TM-C, Labor 1                                  */
/* description                                         */
/*                                                     */
/*******************************************************/

Declarations

Wir definieren die Parameter

${\begin{array}{l}q_{A}={\frac {3\cdot kN}{m}},\\l_{1}={\frac {7\cdot m}{10}},\\EI_{1}=33600\;N\;{{m}^{2}},\\{{l}_{2}}={\frac {21\;m}{40}},\\EI_{2}=16800\;N\;{{m}^{2}},\\{{K}_{A}}=96\;kN\;m,\\{{k}_{C}}={\frac {22\;kN}{m}},\\{{k}_{B}}={\frac {98\;kN}{m}},\\{{q}_{B}}={\frac {12\;N}{mm}},\\{{M}_{B}}=1470\;Nm\end{array}}$.

und die Formfunktionen für die Streckenlast

${\begin{array}{l}{{\phi }_{0}}\left(\xi \right):=1-\xi \\{{\phi }_{1}}\left(\xi \right):=\xi \end{array}}$.

/* system parameter */
units  : [mm = m/1000, cm = m/100];
params : [q[A]=3*N/mm, l[1]=700*mm, EI[1] = 2.1*10^11*N/m^2 * 3*cm*(4*cm)^3/12];
simple : [l[2] = 3/4*l[1], EI[2] = EI[1]/2,
          K[A]=2*EI[1]/l[1], k[C] = 512/229*EI[1]/l[1]^3, k[B] = EI[1]/l[1]^3, 
          q[B] = 4*q[A], M[B] = q[A]*l[1]^2];

params : append(params,makelist(lhs(simple[i])=subst(params,rhs(simple[i])),i,1,length(simple)));
params : subst(units,params);

/* form - functions  */
phi[0](xi) := 1 - xi;
phi[1](xi) :=     xi;

Formfunctions

In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung

$E\;I_{i}w_{i}^{IV}(x_{i})=q(x_{i}),\;\;i=\{1,2\}{\text{ mit }}q(x_{i})=q_{0}\cdot \phi _{0}(\xi )+q_{1}\cdot \phi _{1}(\xi )$,

die wir durch Integration lösen und dann bereichsweise anpassen.

So gilt für Bereich II: q₀ = 0 und q₁ = 0.

Die allgemeine Lösung ist mit

$\displaystyle \phi _{i}(x)={\frac {dw(x)}{dx}}$

... für Bereich I:

${\begin{array}{l}{{w}_{1}}\left(x\right):={\frac {120\cdot {{l}_{1}}\cdot {{C}_{1,0}}+120\cdot {{l}_{1}}\cdot {{C}_{1,1}}\cdot x+60\cdot {{l}_{1}}\cdot {{C}_{1,2}}\cdot {{x}^{2}}+20\cdot {{l}_{1}}\cdot {{C}_{1,3}}\cdot {{x}^{3}}+5\cdot {{l}_{1}}\cdot {{x}^{4}}\cdot {{q}_{A}}+{{x}^{5}}\cdot \left({{q}_{B}}-{{q}_{A}}\right)}{120\cdot {{l}_{1}}\cdot {{\mathit {EI}}_{1}}}}\\{{\phi }_{1}}\left(x\right):={\frac {120\cdot {{l}_{1}}\cdot {{C}_{1,1}}+120\cdot {{l}_{1}}\cdot {{C}_{1,2}}\cdot x+60\cdot {{l}_{1}}\cdot {{C}_{1,3}}\cdot {{x}^{2}}+20\cdot {{l}_{1}}\cdot {{x}^{3}}\cdot {{q}_{A}}+5\cdot {{x}^{4}}\cdot \left({{q}_{B}}-{{q}_{A}}\right)}{120\cdot {{l}_{1}}\cdot {{\mathit {EI}}_{1}}}}\\{{M}_{1}}\left(x\right):=-{\frac {120\cdot {{l}_{1}}\cdot {{C}_{1,2}}+120\cdot {{l}_{1}}\cdot {{C}_{1,3}}\cdot x+60\cdot {{l}_{1}}\cdot {{x}^{2}}\cdot {{q}_{A}}+20\cdot {{x}^{3}}\cdot \left({{q}_{B}}-{{q}_{A}}\right)}{120\cdot {{l}_{1}}}}\\{{Q}_{1}}\left(x\right):=-{\frac {120\cdot {{l}_{1}}\cdot {{C}_{1,3}}+120\cdot {{l}_{1}}\cdot x\cdot {{q}_{A}}+60\cdot {{x}^{2}}\cdot \left({{q}_{B}}-{{q}_{A}}\right)}{120\cdot {{l}_{1}}}}\end{array}}$

... für Bereich II:

${\begin{array}{l}{{w}_{2}}\left(x\right):={\frac {120\cdot {{l}_{2}}\cdot {{C}_{2,0}}+120\cdot {{l}_{2}}\cdot {{C}_{2,1}}\cdot x+60\cdot {{l}_{2}}\cdot {{C}_{2,2}}\cdot {{x}^{2}}+20\cdot {{l}_{2}}\cdot {{C}_{2,3}}\cdot {{x}^{3}}}{120\cdot {{l}_{2}}\cdot {{\mathit {EI}}_{2}}}}\\{{\phi }_{2}}\left(x\right):={\frac {120\cdot {{l}_{2}}\cdot {{C}_{2,1}}+120\cdot {{l}_{2}}\cdot {{C}_{2,2}}\cdot x+60\cdot {{l}_{2}}\cdot {{C}_{2,3}}\cdot {{x}^{2}}}{120\cdot {{l}_{2}}\cdot {{\mathit {EI}}_{2}}}}\\{{M}_{2}}\left(x\right):=-{\frac {120\cdot {{l}_{2}}\cdot {{C}_{2,2}}+120\cdot {{l}_{2}}\cdot {{C}_{2,3}}\cdot x}{120\cdot {{l}_{2}}}}\\{{Q}_{2}}\left(x\right):=-{{C}_{2,3}}\end{array}}$.

/* solve ....*/
dgl : EI[i]*diff(w(x),x,4) = q[0]*phi[0](x/l[i]) + q[1]*phi[1](x/l[i]);
/* generic solution */
displ : solve(integrate(integrate(integrate(integrate(dgl,x),x),x),x),w(x));
sections: [[i=1, %c4=C[1,0], %c3=C[1,1], %c2=C[1,2], %c1=C[1,3], q[0]=q[A], q[1]=q[B]],
           [i=2, %c4=C[2,0], %c3=C[2,1], %c2=C[2,2], %c1=C[2,3], q[0]= 0  , q[1]= 0  ]];

/* section I */
define(  w[1](x),  subst(sections[1],subst(displ,w(x))));
define(Phi[1](x),  diff(w[1](x),x  ));
define(  M[1](x), -EI[1]*diff(w[1](x),x,2));
define(  Q[1](x), -EI[1]*diff(w[1](x),x,3));

/* section II */
define(  w[2](x),  subst(sections[2],subst(displ,w(x))));
define(Phi[2](x),  diff(w[2](x),x  ));
define(  M[2](x), -EI[2]*diff(w[2](x),x,2));
define(  Q[2](x), -EI[2]*diff(w[2](x),x,3));

Boundary Conditions

Für die 2*4 = 8 Integrationskonstanten

$\left[C_{1,0},C_{1,1},C_{1,2},C_{1,3},C_{2,0},C_{2,1},C_{2,2},C_{2,3}\right]$

suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen.

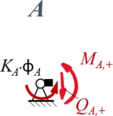
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen.

Aus Rand "A"

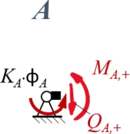
Geometrische Randbedingungen $w_{1}(0)=0$ Kraft- und Momenten-Randbedingungen $K_{A}\cdot \phi _{A}+M_{A,+}=0{\text{ mit }}M_{A,+}=-EI_{1}\cdot w''(x)|_{x=0}$

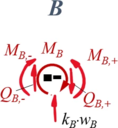
Aus Übergang "B"

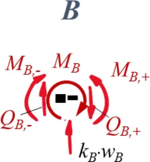
Geometrische Randbedingungen $w_{1}(\ell _{1})=w_{2}(\ell _{1})$ $\phi _{1}(\ell _{1})=\phi _{2}(\ell _{1})$ Kraft- und Momenten-Randbedingungen $-M_{B,-}-M_{B}+M_{B,+}=0$ $-Q_{B,-}-k_{B}\cdot w_{B}+-Q_{B,+}=0$

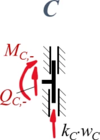
Aus Rand "C"

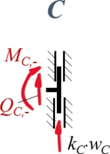
Geometrische Randbedingungen $\phi _{2}(\ell _{2})=0$ Kraft- und Momenten-Randbedingungen $-Q_{C,-}-k_{C}\cdot w_{C}=0$

Und das liefert das Gleichungssystem aus 8 Gleichungen

${\begin{pmatrix}{\frac {{C}_{1,0}}{{\mathit {EI}}_{1}}}=0\\{\frac {{{C}_{1,1}}\cdot {{K}_{A}}}{{\mathit {EI}}_{1}}}-{{C}_{1,2}}=0\\{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{B}}}{120\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{A}}}{30\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{3}}\cdot {{C}_{1,3}}}{6\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{2}}\cdot {{C}_{1,2}}}{2\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}}\cdot {{C}_{1,1}}}{{\mathit {EI}}_{1}}}+{\frac {{C}_{1,0}}{{\mathit {EI}}_{1}}}={\frac {{C}_{2,0}}{{\mathit {EI}}_{2}}}\\{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{B}}}{24\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{A}}}{8\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}^{2}}\cdot {{C}_{1,3}}}{2\cdot {{\mathit {EI}}_{1}}}}+{\frac {{{\ell }_{1}}\cdot {{C}_{1,2}}}{{\mathit {EI}}_{1}}}+{\frac {{C}_{1,1}}{{\mathit {EI}}_{1}}}={\frac {{C}_{2,1}}{{\mathit {EI}}_{2}}}\\{\frac {{{\ell }_{1}}\cdot {{q}_{B}}}{2}}-{\frac {{{C}_{2,0}}\cdot {{k}_{B}}}{{\mathit {EI}}_{2}}}+{\frac {{{\ell }_{1}}\cdot {{q}_{A}}}{2}}-{{C}_{2,3}}+{{C}_{1,3}}=0\\-{{M}_{B}}+{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{B}}}{6}}+{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{A}}}{3}}-{{C}_{2,2}}+{{\ell }_{1}}\cdot {{C}_{1,3}}+{{C}_{1,2}}=0\\{\frac {{{\ell }_{2}^{2}}\cdot {{C}_{2,3}}}{2\cdot {{\mathit {EI}}_{2}}}}+{\frac {{{\ell }_{2}}\cdot {{C}_{2,2}}}{{\mathit {EI}}_{2}}}+{\frac {{C}_{2,1}}{{\mathit {EI}}_{2}}}=0\\-{\frac {{{\ell }_{2}^{3}}\cdot {{C}_{2,3}}\cdot {{k}_{C}}}{6\cdot {{\mathit {EI}}_{2}}}}-{\frac {{{\ell }_{2}^{2}}\cdot {{C}_{2,2}}\cdot {{k}_{C}}}{2\cdot {{\mathit {EI}}_{2}}}}-{\frac {{{\ell }_{2}}\cdot {{C}_{2,1}}\cdot {{k}_{C}}}{{\mathit {EI}}_{2}}}-{\frac {{{C}_{2,0}}\cdot {{k}_{C}}}{{\mathit {EI}}_{2}}}+{{C}_{2,3}}=0\end{pmatrix}}$

für die Integrationskonstanten.

1+1

tmp

Das Gleichungssystem wollen wir als

${\underline {\underline {A}}}\cdot {\underline {x}}={\underline {b}}$

schreiben, also

${\begin{pmatrix}{\frac {1}{{\mathit {EI}}_{1}}}&0&0&0&0&0&0&0\\0&{\frac {{K}_{A}}{{\mathit {EI}}_{1}}}&-1&0&0&0&0&0\\{\frac {1}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}^{2}}{2\cdot {{\mathit {EI}}_{1}}}}&{\frac {{\ell }_{1}^{3}}{6\cdot {{\mathit {EI}}_{1}}}}&-{\frac {1}{{\mathit {EI}}_{2}}}&0&0&0\\0&{\frac {1}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}}{{\mathit {EI}}_{1}}}&{\frac {{\ell }_{1}^{2}}{2\cdot {{\mathit {EI}}_{1}}}}&0&-{\frac {1}{{\mathit {EI}}_{2}}}&0&0\\0&0&0&1&-{\frac {{k}_{B}}{{\mathit {EI}}_{2}}}&0&0&-1\\0&0&1&{{\ell }_{1}}&0&0&-1&0\\0&0&0&0&0&{\frac {1}{{\mathit {EI}}_{2}}}&{\frac {{\ell }_{2}}{{\mathit {EI}}_{2}}}&{\frac {{\ell }_{2}^{2}}{2\cdot {{\mathit {EI}}_{2}}}}\\0&0&0&0&-{\frac {{k}_{C}}{{\mathit {EI}}_{2}}}&-{\frac {{{\ell }_{2}}\cdot {{k}_{C}}}{{\mathit {EI}}_{2}}}&-{\frac {{{\ell }_{2}^{2}}\cdot {{k}_{C}}}{2\cdot {{\mathit {EI}}_{2}}}}&-{\frac {{{\ell }_{2}^{3}}\cdot {{k}_{C}}-6\cdot {{\mathit {EI}}_{2}}}{6\cdot {{\mathit {EI}}_{2}}}}\end{pmatrix}}\cdot {\underline {x}}={\begin{pmatrix}0\\0\\-{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{B}}}{120\cdot {{\mathit {EI}}_{1}}}}-{\frac {{{\ell }_{1}^{4}}\cdot {{q}_{A}}}{30\cdot {{\mathit {EI}}_{1}}}}\\-{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{B}}}{24\cdot {{\mathit {EI}}_{1}}}}-{\frac {{{\ell }_{1}^{3}}\cdot {{q}_{A}}}{8\cdot {{\mathit {EI}}_{1}}}}\\-{\frac {{{\ell }_{1}}\cdot {{q}_{B}}}{2}}-{\frac {{{\ell }_{1}}\cdot {{q}_{A}}}{2}}\\{{M}_{B}}-{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{B}}}{6}}-{\frac {{{\ell }_{1}^{2}}\cdot {{q}_{A}}}{3}}\\0\\0\end{pmatrix}}$

Die Matrix-Elemente sind für die Koeffizientenmatrix

${\begin{array}{l}a_{1,1}=1/EI_{1}\\a_{2,2}=K_{A}/EI_{1}\\a_{2,3}=-1\\a_{3,1}=1/EI_{1}\\a_{3,2}=\ell _{1}/EI_{1}\\a_{3,3}=\ell _{1}^{2}/(2\cdot EI_{1})\\a_{3,4}=\ell _{1}^{3}/(6\cdot EI_{1})\\a_{3,5}=-1/EI_{2}\\a_{4,2}=1/EI_{1}\\a_{4,3}=\ell _{1}/EI_{1}\\a_{4,4}=\ell _{1}^{2}/(2\cdot EI_{1})\\a_{4,6}=-1/EI_{2}\\a_{5,4}=1\\a_{5,5}=-k_{B}/EI_{2}\\a_{5,8}=-1\\a_{6,3}=1\\a_{6,4}=\ell _{1}\\a_{6,7}=-1\\a_{7,6}=1/EI_{2}\\a_{7,7}=\ell _{2}/EI_{2}\\a_{7,8}=\ell _{2}^{2}/(2\cdot EI_{2})\\a_{8,5}=-k_{C}/EI_{2}\\a_{8,6}=-(\ell _{2}\cdot k_{C})/EI_{2}\\a_{8,7}=-(\ell _{2}^{2}\cdot k_{C})/(2\cdot EI_{2})\\a_{8,8}=-(\ell _{2}^{3}\cdot k_{C}-6\cdot EI_{2})/(6\cdot EI_{2})\\\end{array}}$

und für die rechte Seite

${\begin{array}{l}b_{1}=0\\b_{2}=0\\b_{3}=(-(\ell _{1}^{4}\cdot q_{B})/(120\cdot EI_{1}))-(\ell _{1}^{4}\cdot q_{A})/(30\cdot EI_{1})\\b_{4}=(-(\ell _{1}^{3}\cdot q_{B})/(24\cdot EI_{1}))-(\ell _{1}^{3}\cdot q_{A})/(8\cdot EI_{1})\\b_{5}=(-(\ell _{1}\cdot q_{B})/2)-(\ell _{1}\cdot q_{A})/2\\b_{6}=M_{B}-(\ell _{1}^{2}\cdot q_{B})/6-(\ell _{1}^{2}\cdot q_{A})/3\\b_{7}=0\\b_{8}=0\end{array}}$

Prepare for Solver

Text

1+1

tmp

Das Lösen des Gleichungssystems liefert

${\begin{array}{l}{{C}_{1,0}}=0,\\{{C}_{1,1}}=246.1\;N{{m}^{2}},\\{{C}_{1,2}}=703.2\;Nm,\\{{C}_{1,3}}=-2404.3\;N,\\{{C}_{2,0}}=127.6\;Nm^{3},\\{{C}_{2,1}}=224.7\;Nm^{2},\\{{C}_{2,2}}=-979.8\;Nm,\\{{C}_{2,3}}=2101.8N\end{array}}$

Solving

Text

1+1

tmp

Und die Ergebnisse können wir uns anschauen ...

... für w(x):

Biegelinie w(x)

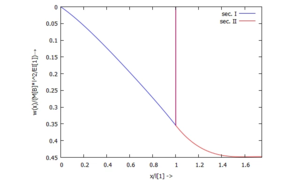
... für Φ(x):

Kippung w'(x)

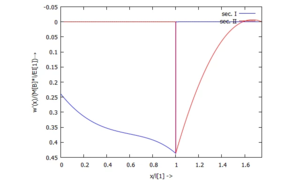
... für M(x):

Biegemoment M(x)

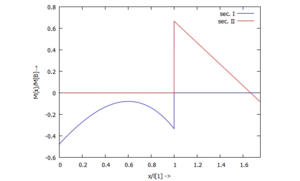
... für Q(x):

Querkraft Q(x)

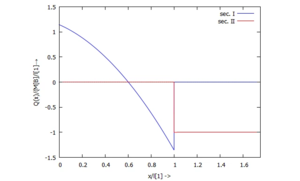
Post-Processing

Text

1+1

---

Links

• ...

Literature

• ...