Gelöste Aufgaben/Kw98: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Ein Stab ''ABC'' ist durch eine lineare veränderliche Streckenlast ''q'' mit den Eckwerten ''q<sub>A</sub>'' in ''A'' und ''q<sub>B</sub>'' in ''B'' sowie dem Moment ''M<sub>B</sub>'' in ''B'' belastet. Der Stab (E-Modul: ''E'') besteht aus zwei Sektionen mit den Längen ''l<sub>1</sub>'' bzw. ''l<sub>2</sub>'' sowie den Flächenmomenten ''I<sub>1</sub>'' bzw. ''I<sub>2</sub>''. Der Stab ist in ''A'' durch ein gelenkiges Festlager, in ''C'' durch eine Schiebehülse gelagert, in ''B'' sind die beiden Sektionen fest miteinander verbunden. Die Feder in ''A'' ist eine Drehfester mit Steifigkeit ''K<sub>A</sub>'', die Federn in ''B'' und ''C'' sind Translationsfedern mit den Steifigkeiten ''k<sub>B</sub>, k<sub>C</sub>''. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw98-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | ||
Gesucht ist | Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken. | ||
</onlyinclude> | </onlyinclude> | ||
[[Datei:Kw98-02.png|mini|Systemparameter]] | |||
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter: | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Die Aufgabe ist ein klassisches Randwertproblem: | |||
<table class="wikitable" style="background-color:white;"> | # zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast ''q'' belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehung<blockquote><math>E\; I_i w_i^{IV}(x_i) = q(x_i) ,\;\; i=\{1,2\}</math></blockquote>berschrieben wird. | ||
<tr><th>Rand<br/>A</th><th>Bereich I</th><th>Übergang<br/>B</th><th>Bereich II</th><th>Rand<br/>C</th></tr> | # Rand- und Übergangsbedingungen in den Punkten A, B, C | ||
<tr><td></td><td>[[Datei:Kw98-11AB.png|rahmenlos|alternativtext=|200x200px]]</td><td></td><td>[[Datei:Kw98-11BC.png|rahmenlos|alternativtext=| | |||
<tr><td>[[Datei:Kw98-11A.png|116x116px|rahmenlos|alternativtext=]]</td><td></td><td>[[Datei:Kw98-11B.png|rahmenlos|alternativtext=|128x128px]]</td><td></td><td>[[Datei:Kw98-11C.png|rahmenlos|alternativtext=| | Wir verwenden ''x<sub>i</sub>'' und ''ξ<sub>i</sub>'' als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:<table class="wikitable" style="background-color:white;"> | ||
<tr><th>Rand<br />A</th><th>Bereich I</th><th>Übergang<br />B</th><th>Bereich II</th><th>Rand<br />C</th></tr> | |||
<tr><td></td><td>[[Datei:Kw98-11AB.png|rahmenlos|alternativtext=|200x200px]]</td><td></td><td>[[Datei:Kw98-11BC.png|rahmenlos|alternativtext=|150x150px]]</td><td></td></tr> | |||
<tr><td>[[Datei:Kw98-11A.png|116x116px|rahmenlos|alternativtext=]]</td><td></td><td>[[Datei:Kw98-11B.png|rahmenlos|alternativtext=|128x128px]]</td><td></td><td>[[Datei:Kw98-11C.png|rahmenlos|alternativtext=|140x140px]] | |||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
| Zeile 29: | Zeile 35: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Diese Aufgabe mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] in [[Gelöste Aufgaben/Kw96|KW96]] gelöst.<!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 51: | Zeile 58: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung | ||
<math>E\; I_i w_i^{IV}(x_i) = q(x_i) ,\;\; i=\{1,2\} \text{ mit } q(x_i) = q_0\cdot\phi_0(\xi) + q_1\cdot\phi_1(\xi)</math>, | |||
die wir durch Integration lösen und dann bereichsweise anpassen. | |||
So gilt für Bereich II: ''q<sub>0</sub> = 0'' und ''q<sub>1</sub> = 0''. | |||
Die allgemeine Lösung ist mit | |||
<math>\displaystyle \phi_i(x) = \frac{dw(x)}{dx}</math> | |||
... für Bereich I: | |||
<math>\begin{array}{l} {{w}_{1}}\left( x\right) :=\frac{120\cdot {{l}_{1}}\cdot {{C}_{1,0}}+120\cdot {{l}_{1}}\cdot {{C}_{1,1}}\cdot x+60\cdot {{l}_{1}}\cdot {{C}_{1,2}}\cdot {{x}^{2}}+20\cdot {{l}_{1}}\cdot {{C}_{1,3}}\cdot {{x}^{3}}+5\cdot {{l}_{1}}\cdot {{x}^{4}}\cdot {{q}_{A}}+{{x}^{5}}\cdot \left( {{q}_{B}}-{{q}_{A}}\right) }{120\cdot {{l}_{1}}\cdot {{\mathit{EI}}_{1}}}\\ {{\phi}_{1}}\left( x\right) :=\frac{120\cdot {{l}_{1}}\cdot {{C}_{1,1}}+120\cdot {{l}_{1}}\cdot {{C}_{1,2}}\cdot x+60\cdot {{l}_{1}}\cdot {{C}_{1,3}}\cdot {{x}^{2}}+20\cdot {{l}_{1}}\cdot {{x}^{3}}\cdot {{q}_{A}}+5\cdot {{x}^{4}}\cdot \left( {{q}_{B}}-{{q}_{A}}\right) }{120\cdot {{l}_{1}}\cdot {{\mathit{EI}}_{1}}}\\ {{M}_{1}}\left( x\right) :=-\frac{120\cdot {{l}_{1}}\cdot {{C}_{1,2}}+120\cdot {{l}_{1}}\cdot {{C}_{1,3}}\cdot x+60\cdot {{l}_{1}}\cdot {{x}^{2}}\cdot {{q}_{A}}+20\cdot {{x}^{3}}\cdot \left( {{q}_{B}}-{{q}_{A}}\right) }{120\cdot {{l}_{1}}}\\ {{Q}_{1}}\left( x\right) :=-\frac{120\cdot {{l}_{1}}\cdot {{C}_{1,3}}+120\cdot {{l}_{1}}\cdot x\cdot {{q}_{A}}+60\cdot {{x}^{2}}\cdot \left( {{q}_{B}}-{{q}_{A}}\right) }{120\cdot {{l}_{1}}} \end{array}</math> | |||
... für Bereich II: | |||
<math>\begin{array}{l} {{w}_{2}}\left( x\right) :=\frac{120\cdot {{l}_{2}}\cdot {{C}_{2,0}}+120\cdot {{l}_{2}}\cdot {{C}_{2,1}}\cdot x+60\cdot {{l}_{2}}\cdot {{C}_{2,2}}\cdot {{x}^{2}}+20\cdot {{l}_{2}}\cdot {{C}_{2,3}}\cdot {{x}^{3}}}{120\cdot {{l}_{2}}\cdot {{\mathit{EI}}_{2}}}\\ {{\phi}_{2}}\left( x\right) :=\frac{120\cdot {{l}_{2}}\cdot {{C}_{2,1}}+120\cdot {{l}_{2}}\cdot {{C}_{2,2}}\cdot x+60\cdot {{l}_{2}}\cdot {{C}_{2,3}}\cdot {{x}^{2}}}{120\cdot {{l}_{2}}\cdot {{\mathit{EI}}_{2}}}\\ {{M}_{2}}\left( x\right) :=-\frac{120\cdot {{l}_{2}}\cdot {{C}_{2,2}}+120\cdot {{l}_{2}}\cdot {{C}_{2,3}}\cdot x}{120\cdot {{l}_{2}}}\\ {{Q}_{2}}\left( x\right) :=-{{C}_{2,3}} \end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
| Zeile 62: | Zeile 88: | ||
==tmp== | ==tmp== | ||
Für die 2*4 = 8 Integrationskonstanten | |||
<math>\left[ C_{1,0},C_{1,1},C_{1,2},C_{1,3},C_{2,0},C_{2,1},C_{2,2},C_{2,3}\right]</math> | |||
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen. | |||
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen. | |||
====Aus Rand "A"==== | ====Aus Rand "A"==== | ||
<table class="wikitable" style="background-color:white;"> | <table class="wikitable" style="background-color:white;"> | ||
<tr><td>[[Datei:Kw98-11A.png|rahmenlos|alternativtext=| | <tr><td>[[Datei:Kw98-11A.png|rahmenlos|alternativtext=|134x134px]] | ||
</td><td>''Geometrische Randbedingungen'' | </td><td>''Geometrische Randbedingungen'' | ||
# <math>w_1(0)=0</math> | |||
''Kraft- und Momenten-Randbedingungen'' | ''Kraft- und Momenten-Randbedingungen'' | ||
# <math> | #<math>K_A\cdot \phi_A + M_{A,+} = 0 \text{ mit } M_{A,+} = - EI_1\cdot w''(x)|_{x=0}</math> | ||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
| Zeile 79: | Zeile 110: | ||
====Aus Übergang "B"==== | ====Aus Übergang "B"==== | ||
<table class="wikitable" style="background-color:white;"> | <table class="wikitable" style="background-color:white;"> | ||
<tr><td>[[Datei:Kw98-11B.png|rahmenlos|alternativtext=| | <tr><td>[[Datei:Kw98-11B.png|rahmenlos|alternativtext=|162x162px]] | ||
</td><td>''Geometrische Randbedingungen'' | </td><td>''Geometrische Randbedingungen'' | ||
# <math>w_1(\ell_1)=w_2(\ell_1)</math> | # <math>w_1(\ell_1)=w_2(\ell_1)</math> | ||
| Zeile 86: | Zeile 117: | ||
''Kraft- und Momenten-Randbedingungen'' | ''Kraft- und Momenten-Randbedingungen'' | ||
# <math>-M_{B,-} + M_{B,+} = 0</math> | #<math>-M_{B,-} - M_{B} + M_{B,+} = 0</math> | ||
# <math>-Q_{B,-} - | #<math>-Q_{B,-}-k_B\cdot w_B + -Q_{B,+} = 0</math> | ||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
| Zeile 93: | Zeile 124: | ||
====Aus Rand "C"==== | ====Aus Rand "C"==== | ||
<table class="wikitable" style="background-color:white;"> | <table class="wikitable" style="background-color:white;"> | ||
<tr><td>[[Datei:Kw98-11C.png|rahmenlos|alternativtext=| | <tr><td>[[Datei:Kw98-11C.png|rahmenlos|alternativtext=|154x154px]] | ||
</td><td>''Geometrische Randbedingungen'' | </td><td>''Geometrische Randbedingungen'' | ||
# <math> | #<math>\phi_2(\ell_2)=0</math> | ||
''Kraft- und Momenten-Randbedingungen'' | ''Kraft- und Momenten-Randbedingungen'' | ||
# <math> | #<math>-Q_{C,-} -k_C\cdot w_C = 0</math> | ||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
Und das liefert das Gleichungssystem aus 8 Gleichungen | |||
<math>\begin{pmatrix}\frac{{{C}_{1,0}}}{{{\mathit{EI}}_{1}}}=0\\ \frac{{{C}_{1,1}}\cdot {{K}_{A}}}{{{\mathit{EI}}_{1}}}-{{C}_{1,2}}=0\\ \frac{{{\ell}_{1}^{4}}\cdot {{q}_{B}}}{120\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}^{4}}\cdot {{q}_{A}}}{30\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}^{3}}\cdot {{C}_{1,3}}}{6\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}^{2}}\cdot {{C}_{1,2}}}{2\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}}\cdot {{C}_{1,1}}}{{{\mathit{EI}}_{1}}}+\frac{{{C}_{1,0}}}{{{\mathit{EI}}_{1}}}=\frac{{{C}_{2,0}}}{{{\mathit{EI}}_{2}}}\\ \frac{{{\ell}_{1}^{3}}\cdot {{q}_{B}}}{24\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}^{3}}\cdot {{q}_{A}}}{8\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}^{2}}\cdot {{C}_{1,3}}}{2\cdot {{\mathit{EI}}_{1}}}+\frac{{{\ell}_{1}}\cdot {{C}_{1,2}}}{{{\mathit{EI}}_{1}}}+\frac{{{C}_{1,1}}}{{{\mathit{EI}}_{1}}}=\frac{{{C}_{2,1}}}{{{\mathit{EI}}_{2}}}\\ \frac{{{\ell}_{1}}\cdot {{q}_{B}}}{2}-\frac{{{C}_{2,0}}\cdot {{k}_{B}}}{{{\mathit{EI}}_{2}}}+\frac{{{\ell}_{1}}\cdot {{q}_{A}}}{2}-{{C}_{2,3}}+{{C}_{1,3}}=0\\ -{{M}_{B}}+\frac{{{\ell}_{1}^{2}}\cdot {{q}_{B}}}{6}+\frac{{{\ell}_{1}^{2}}\cdot {{q}_{A}}}{3}-{{C}_{2,2}}+{{\ell}_{1}}\cdot {{C}_{1,3}}+{{C}_{1,2}}=0\\ \frac{{{\ell}_{2}^{2}}\cdot {{C}_{2,3}}}{2\cdot {{\mathit{EI}}_{2}}}+\frac{{{\ell}_{2}}\cdot {{C}_{2,2}}}{{{\mathit{EI}}_{2}}}+\frac{{{C}_{2,1}}}{{{\mathit{EI}}_{2}}}=0\\ -\frac{{{\ell}_{2}^{3}}\cdot {{C}_{2,3}}\cdot {{k}_{C}}}{6\cdot {{\mathit{EI}}_{2}}}-\frac{{{\ell}_{2}^{2}}\cdot {{C}_{2,2}}\cdot {{k}_{C}}}{2\cdot {{\mathit{EI}}_{2}}}-\frac{{{\ell}_{2}}\cdot {{C}_{2,1}}\cdot {{k}_{C}}}{{{\mathit{EI}}_{2}}}-\frac{{{C}_{2,0}}\cdot {{k}_{C}}}{{{\mathit{EI}}_{2}}}+{{C}_{2,3}}=0\end{pmatrix} | |||
</math> | |||
<!--------------------------------------------------------------------------------> | für die Integrationskonstanten.<!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Boundary Conditions | {{MyCodeBlock|title=Boundary Conditions | ||
|text=Text | |text=Text | ||
| Zeile 116: | Zeile 150: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Das Gleichungssystem wollen wir als | ||
<math>\underline{\underline{A}}\cdot\underline{x}= \underline{b}</math> | |||
schreiben, also | |||
<math>\begin{pmatrix}\frac{1}{{{\mathit{EI}}_{1}}} & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & \frac{{{K}_{A}}}{{{\mathit{EI}}_{1}}} & -1 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{{{\mathit{EI}}_{1}}} & \frac{{{\ell}_{1}}}{{{\mathit{EI}}_{1}}} & \frac{{{\ell}_{1}^{2}}}{2\cdot {{\mathit{EI}}_{1}}} & \frac{{{\ell}_{1}^{3}}}{6\cdot {{\mathit{EI}}_{1}}} & -\frac{1}{{{\mathit{EI}}_{2}}} & 0 & 0 & 0\\ 0 & \frac{1}{{{\mathit{EI}}_{1}}} & \frac{{{\ell}_{1}}}{{{\mathit{EI}}_{1}}} & \frac{{{\ell}_{1}^{2}}}{2\cdot {{\mathit{EI}}_{1}}} & 0 & -\frac{1}{{{\mathit{EI}}_{2}}} & 0 & 0\\ 0 & 0 & 0 & 1 & -\frac{{{k}_{B}}}{{{\mathit{EI}}_{2}}} & 0 & 0 & -1\\ 0 & 0 & 1 & {{\ell}_{1}} & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1}{{{\mathit{EI}}_{2}}} & \frac{{{\ell}_{2}}}{{{\mathit{EI}}_{2}}} & \frac{{{\ell}_{2}^{2}}}{2\cdot {{\mathit{EI}}_{2}}}\\ 0 & 0 & 0 & 0 & -\frac{{{k}_{C}}}{{{\mathit{EI}}_{2}}} & -\frac{{{\ell}_{2}}\cdot {{k}_{C}}}{{{\mathit{EI}}_{2}}} & -\frac{{{\ell}_{2}^{2}}\cdot {{k}_{C}}}{2\cdot {{\mathit{EI}}_{2}}} & -\frac{{{\ell}_{2}^{3}}\cdot {{k}_{C}}-6\cdot {{\mathit{EI}}_{2}}}{6\cdot {{\mathit{EI}}_{2}}}\end{pmatrix}\cdot\underline{x}=\begin{pmatrix}0\\ 0\\ -\frac{{{\ell}_{1}^{4}}\cdot {{q}_{B}}}{120\cdot {{\mathit{EI}}_{1}}}-\frac{{{\ell}_{1}^{4}}\cdot {{q}_{A}}}{30\cdot {{\mathit{EI}}_{1}}}\\ -\frac{{{\ell}_{1}^{3}}\cdot {{q}_{B}}}{24\cdot {{\mathit{EI}}_{1}}}-\frac{{{\ell}_{1}^{3}}\cdot {{q}_{A}}}{8\cdot {{\mathit{EI}}_{1}}}\\ -\frac{{{\ell}_{1}}\cdot {{q}_{B}}}{2}-\frac{{{\ell}_{1}}\cdot {{q}_{A}}}{2}\\ {{M}_{B}}-\frac{{{\ell}_{1}^{2}}\cdot {{q}_{B}}}{6}-\frac{{{\ell}_{1}^{2}}\cdot {{q}_{A}}}{3}\\ 0\\ 0\end{pmatrix} | |||
</math> | |||
Die Matrix-Elemente sind für die Koeffizientenmatrix | |||
<math>\begin{array}{l} a_{1,1} = 1/EI_{1}\\ a_{2,2} = K_{A}/EI_{1}\\ a_{2,3} = -1\\ a_{3,1} = 1/EI_{1}\\ a_{3,2} = \ell_{1}/EI_{1}\\ a_{3,3} = \ell_{1}^2/(2\cdot EI_{1})\\ a_{3,4} = \ell_{1}^3/(6\cdot EI_{1})\\ a_{3,5} = -1/EI_{2}\\ a_{4,2} = 1/EI_{1}\\ a_{4,3} = \ell_{1}/EI_{1}\\ a_{4,4} = \ell_{1}^2/(2\cdot EI_{1})\\ a_{4,6} = -1/EI_{2}\\ a_{5,4} = 1\\ a_{5,5} = -k_{B}/EI_{2}\\ a_{5,8} = -1\\ a_{6,3} = 1\\ a_{6,4} = \ell_{1}\\ a_{6,7} = -1\\ a_{7,6} = 1/EI_{2}\\ a_{7,7} = \ell_{2}/EI_{2}\\ a_{7,8} = \ell_{2}^2/(2\cdot EI_{2})\\ a_{8,5} = -k_{C}/EI_{2}\\ a_{8,6} = -(\ell_{2}\cdot k_{C})/EI_{2}\\ a_{8,7} = -(\ell_{2}^2\cdot k_{C})/(2\cdot EI_{2})\\ a_{8,8} = -(\ell_{2}^3\cdot k_{C}-6\cdot EI_{2})/(6\cdot EI_{2})\\ \end{array}</math> | |||
und für die rechte Seite | |||
<math>\begin{array}{l} b_{1} = 0\\ b_{2} = 0\\ b_{3} = (-(\ell_{1}^4\cdot q_{B})/(120\cdot EI_{1}))-(\ell_{1}^4\cdot q_{A})/(30\cdot EI_{1})\\ b_{4} = (-(\ell_{1}^3\cdot q_{B})/(24\cdot EI_{1}))-(\ell_{1}^3\cdot q_{A})/(8\cdot EI_{1})\\ b_{5} = (-(\ell_{1}\cdot q_{B})/2)-(\ell_{1}\cdot q_{A})/2\\ b_{6} = M_{B}-(\ell_{1}^2\cdot q_{B})/6-(\ell_{1}^2\cdot q_{A})/3\\ b_{7} = 0\\ b_{8} = 0 \end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Prepare for Solver | {{MyCodeBlock|title=Prepare for Solver | ||
|text=Text | |text=Text | ||
| Zeile 127: | Zeile 178: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Das Lösen des Gleichungssystems liefert | ||
<math>\begin{array}{l} {{C}_{1,0}}=0,\\{{C}_{1,1}}=246.1 \; N {{m}^{2}},\\{{C}_{1,2}}=703.2\; N m,\\{{C}_{1,3}}=-2404.3\; N,\\{{C}_{2,0}}=127.6 \; N m^3,\\{{C}_{2,1}}=224.7\; N m^2,\\{{C}_{2,2}}=-979.8 \; N m,\\{{C}_{2,3}}=2101.8 N \end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 137: | Zeile 191: | ||
==tmp== | ==tmp== | ||
Und die Ergebnisse können wir uns anschauen ... | |||
==== ... für w(x): ==== | ==== ... für w(x): ==== | ||
| Zeile 159: | Zeile 214: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
Version vom 31. März 2021, 12:05 Uhr
Aufgabenstellung
Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten qA in A und qB in B sowie dem Moment MB in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l1 bzw. l2 sowie den Flächenmomenten I1 bzw. I2. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit KA, die Federn in B und C sind Translationsfedern mit den Steifigkeiten kB, kC.
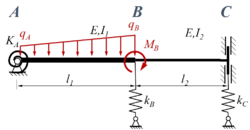
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken.
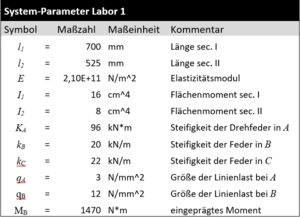
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Lösung mit Maxima
Die Aufgabe ist ein klassisches Randwertproblem:
- zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehungberschrieben wird.
- Rand- und Übergangsbedingungen in den Punkten A, B, C
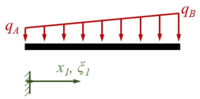
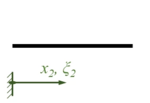
Wir verwenden xi und ξi als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:
| Rand A | Bereich I | Übergang B | Bereich II | Rand C |
|---|---|---|---|---|
 |  | |||
 |  | 
|
tmp
Diese Aufgabe mit der Methode der Finiten Elemente in KW96 gelöst.
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung
,
die wir durch Integration lösen und dann bereichsweise anpassen.
So gilt für Bereich II: q0 = 0 und q1 = 0.
Die allgemeine Lösung ist mit
... für Bereich I:
... für Bereich II:
Formfunctions
Text
1+1
tmp
Für die 2*4 = 8 Integrationskonstanten
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen.
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen.
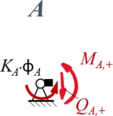
Aus Rand "A"
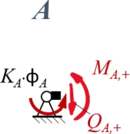
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
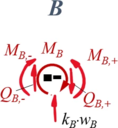
Aus Übergang "B"
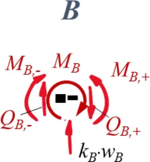
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
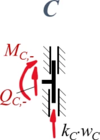
Aus Rand "C"
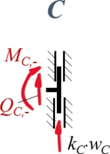
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
Und das liefert das Gleichungssystem aus 8 Gleichungen
für die Integrationskonstanten.
Boundary Conditions
Text
1+1
tmp
Das Gleichungssystem wollen wir als
schreiben, also
Die Matrix-Elemente sind für die Koeffizientenmatrix
und für die rechte Seite
Prepare for Solver
Text
1+1
tmp
Das Lösen des Gleichungssystems liefert
Solving
Text
1+1
tmp
Und die Ergebnisse können wir uns anschauen ...
... für w(x):
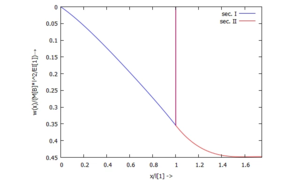
... für Φ(x):
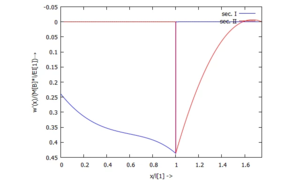
... für M(x):
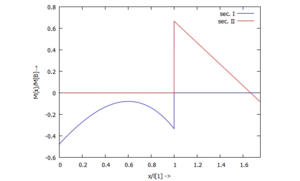
... für Q(x):
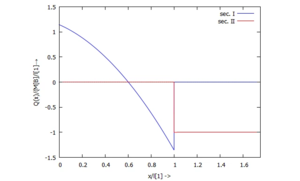
Post-Processing
Text
1+1
Links
- ...
Literature
- ...